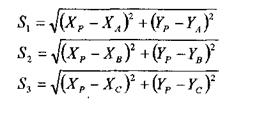определяемого с основного исходного

определяемого с дополнительного

среднего арифметического из двух определений
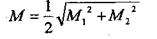
Контроль:
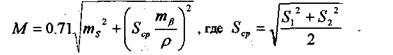
Для оценки точности принять mβ =10", ms вычислить по формуле
ms=(10+5·10-6Sср)мм
Значение Scp взять из таблицы, округлив до целых метров.
Вычисление координат определяемых пунктов.
| Определяемые пункты | Углы от исходного направления до направления на определяемые пункты (левые). | Дирекцио-нный угол | Рассто- яние | Приращения координат | Координаты | ||
| ΔХ | ΔY | X | Y | ||||
| 264° 00' 13" 263 58 17 | 37° 02' 39" 37 01 55 | 6737,50 6732,57 | Средние | ||||
| 352° 11' 14" 352 13 49 | 4450,10 4448,36 | Средние | |||||
| 55° 55' 16" 55 59 56 | 2204,78 2208,34 | Средние | |||||
| 104° 08' 41" 104 07 01 | 1415,09 1420,16 | Средние | |||||
| 180° 58' 20" 180 52 50 | 4076,66 4077,69 | Средние | |||||
ВОПРОСЫДЛЯ САМОПРОВЕРКИ
1. В каких случаях возникает необходимость в решении задачи по снесению координат с вершины знака на землю?
2. Какие виды может иметь схематический чертёж к задаче по снесению координат
с вершины знака на землю?
3. Какие исходные данные необходимы для решения задачи по передаче координат
с вершины знака на землю? Какие нужно выполнить измерения для этой цели?
|
|
4. В каких пределах допускается величина углов, лежащих против измеренных
базисов вспомогательных треугольников?
5. Какое допускается расхождение в вычисленных значениях расстояния из
двух треугольников, если измерение базисов выполнено с точностью 1:2 000?
6. Напишите и объясните формулу СКП положения пункта, определяемого
снесением координат с вершины знака на землю.
7. В чём сущность прямой засечке? Изобразите схему решения задачи по
формулам Юнга?
8. Как зависит точность определения положения пункта от угла засечки?
9. В каких случаях решают задачу по формулам Юнга?
10. Напишите и объясните формулы Юнга.
11. Как осуществляют контроль вычислений при решении задачи по формулам
Юнга? Какова величина допустимых расхождений?
12. В чём состоит контроль измерений при решении задачи по формулам Юнга?
Напишите формулы для обоих способов контроля.
13. Напишите и объясните формулу СКП положения пункта, определяемого
прямой засечкой.
14. В каких случаях решают задачу по формулам Гаусса?
15. Изобразите схему решения задачи по формулам Гаусса?
16. Напишите и объясните формулы Гаусса.
17. Когда применяют формулы с тангенсами и когда с котангенсами дирекционных
углов?
18. Объясните контроль решения задачи по формулам Гаусса.
19. Напишите и объясните СКП положения пункта, определяемого прямой'
засечкой.
20. Объясните благоприятные и неблагоприятные случаи определения положения
точки обратной засечки?
21.Изобразите и объясните схему решения задачи обратной засечкой.
22. Объясните контроль определения координат пункта обратной засечкой.
|
|
23. Напишите и объясните формулу СКП положения пункта, определяемого
обратной засечкой.
24. Изобразите и объясните схему решения задачи линейной засечкой.
25.Объясните контроль определения координат пункта линейной засечкой.
26. Изобразите и объясните схему решения задачи лучевым способом.
27. Объясните контроль определения координат пункта лучевым способом.
28. Напишите и объясните формулы СКП положения пункта, определяемого
лучевым способом.
ЛИТЕРАТУРА
1. Маслов А.В., Гордеев А. В., Батраков Ю.Г. Геодезия. М, КолосС, 2006 г.
2. Батраков Ю.Г. Геодезические сети специального назначения, М., Картгорцентр-
Геодезиздат, 1999 г.
3. Неумывакин Ю.К., Смирнов А.С. Практикум по геодезии. М. КолосС, 2008 г.Недра, 1985г.
ИСХОДНЫЕ ДАННЫЕ
Лучевой способ
| Названия пунктов состояния | Дирекционный угол на п.Тудорово | Координаты | |
| X | Y | ||
| Антоновка осн. Антоновка доп. | 133° 02'26" 133°03'38" | 52 478,40 52 481,55 | 60 743,81 60 748,06 |
Исходные дирекционные углы увеличить на величину N +10', т.е.:
133°03'38'+ (N +10')
133° 02'26"+ (N +10')
Все измеренные расстояния увеличить на величину N + 10м, например:
6737,50 +(N·10м)
6732,57 +(N·10м)
Снесение (передача) координат с вершины знака на земли

| 55° 20' 00,4" | 76° 48' 29,7" | 78° 23' 50,9" | 67° 13' 31,3" | |
| 54 37 18,4 | 78 16 16,2 | 77 33 21,9 | 68 49 04,7 | |
| 53 52 48,4 | 79 44 34,2 | 76 38 29,5 | 70 27 45,1 | |
| 53 06 39,4 | 81 13 17,2 | 75 39 17,1 | 72 09 31,5 | |
| 52 19 00,9 | 82 42 18,0 | 74 35 49,3 | 73 54 21,6 | |
| 51 30 02,1 | 84 11 29,7 | 73 28 12,1 | 75 42 11,7 | |
| 50 39 52,5 | 85 40 45,0 | 72 16 33,3 | 77 32 56,3 | |
| 49 48 41,5 | 87 09 56,8 | 71 01 02,1 | 79 26 28,1 | |
| 48 56 38,4 | 88 38 57,8 | 69 41 49,9 | 81 22 38,3 | |
| 48 03 52,3 | 90 07 40,9 | 68 19 09.4 | 83 21 15,9 | |
| 47 10 32,4 | 91 35 59,2 | 66 53 15,4 | 85 22 08,2 | |
| 46 16 47,1 | 93 03 46,0 | 65 24 24,5 | 87 25 00,6 | |
| 45 22 45,1 | 94 30 54,6 | 63 52 54,7 | 89 29 37,0 | |
| 44 38 34,2 | 95 57 19,0 | 62 19 05,8 | 91 35 39,4 | |
| 43 34 22,3 | 97 22 53,1 | 60 43 18,5 | 93 42 48,9 | |
| 42 40 16,5 | 98 47 31,5 | 59 05 54.9 | 95 50 45,0 | |
| 41 46 23,6 | 100 11 08,9 | 57 27 17,5 | 97 59 07,0 | |
| 40 52 50,1 | 101 33 40,8 | 55 47 49,4 | 100 07 33,4 | |
| 39 59 41,7 | 102 55 02,6 | 54 07 53,6 | 102 15 42,7 | |
| 39 07 03,8 | 104 15 10,7 | 52 27 52,7 | 104 23 13,8 | |
| 38 15 01,3 | 105 34 01,5 | 50 48 08,8 | 106 29 46,0 | |
| 37 23 38,6 | 106 51 32,0 | 49 09 02,8 | 108 34 59,8 | |
| 36 32 59,6 | 108 07 39,6 | 47 30 54,4 | ПО 38 36,8 | |
| 35 43 07,7 | 109 22 22,2 | 45 54 01,8 | 112 40 20,1 | |
| 34 54 06,0 | 110 35 38,1 | 44 18 41,7^ | 114 39 54,5 |
|
|
| Продолжение |

| 79 ' 05 01,4 | 145 51 33,3 | 60,52 | 48,67 | |
| 78 19 21,1 | 145 05 04,8 | 60,32 | 47,88 | |
| 77 34 57,2 | 144 19 32,6 | 60,16 | 47,13 | |
| 76 51 47,4 | 143 35 14,4 | 60,04 | 46,42 | |
| 76 09 49,2 | 142 52 07,9 | 59,96 | 45,75 | |
| 75 29 00,5 | 142 10 10,8 | 59,92 | 45,13 | |
| 74 49 19,0 | 141 29 20,9 | 59,92 | 44,55 | |
| 74 10 42,4 | 140 49 35,9 | 59,06 | 44,02 | |
| 73 33 08,8 | 140 10 53,7 | 60,04 | 43,54 | |
| 72 56 35,9 | 139 33 12,3 | 60,16 | 43,11 | |
| 72 21 01,9 | 138 56 29,6 | 60,32 | 42,73 | |
| 71 46 24,6 | 138 20 43,7 | 60,52 | 42,41 | |
| 71 12 42,3 | 137 45 52,8 | 60,76 | 42,14 | |
| 70 39 53,2 | 137 11 54,9 | 61,04 | 41,92 | |
| 70 07 55,3 | 136 38 48,2 | 61,35 | 41,77 | |
| 69 36 47,1 | 136 06 31,2 | 61,71 | 41,67 | |
| 69 06 26,8 | 135 35 02,1 | 62,10 | 41,63 | |
| 68 36 53,0 | 135 04 19,4 | 62,53 | 41,65 | |
| 68 08 03,9 | 134 34 21,4 | 62,99 | 41,72 | |
| 67 39 58,1 | 134 05 06,7 | 63,48 | 41,85 | |
| 67 12 34,3 | 133 36 33,8 | 64,02 | 42,04 | |
| 66 45 51,0 | 133 08 41,4 | 64,58 | 42,29 | |
| 66 19 46,8 | 132 41 28,1 | 65,18 | 42,59 | |
| 65 54 20,5 | 132 14 52,7 | 65,81 | 42,95 | |
| 65 29 30,8 | 131 48 53,9 | 66,46 | 43,36 |
Обратная засечка.
| № Варианта | 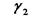
| 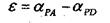
|
| 202°37'42" | 54°44 '09" | |
| 202 42 42 | 54 40 35 | |
| 202 46 27 | 54 37 53 | |
| 202 50 12 | 54 35 11 | |
| 202 53 57 | 54 32 29 | |
| 202 57 42 | 54 29 47 | |
| 203 01 27 | 54 27 08 | |
| 203 05 52 | 54 24 29 | |
| 203 08 47 | 54 21 50 | |
| 203 12 22 | 54 19 11 | |
| 203 16 17 | 54 16 32 | |
| 203 20 12 | 54 13 53 | |
| 203 23 57 | 54 11 14 | |
| 203 27 42 | 54 08 35 | |
| : 2033127 | 54 05 58 | |
| 203 35 12 | 54 03 21 | |
| 203 3857 | 54 00 45 | |
| 53 58 10 | ||
| 203 46 27 | 53 55 35 | |
| 203 50 12 | 53 55 00 |
Прямая засечка.
| № варианта | Формулы Гаусса | Формулы Юнга | ||
| С | А | 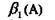
| 
| |
| 261°49'40" | 0°26'30" | 103°19'35" | 92°34'12" | |
| 261 4900 | 103 19 15 | 92 33 32 | ||
| 261 48 20 | 103 18 55 | 92 32 52 | ||
| 261 4740 | 103 18 35 | 92 32 12 | ||
| 261 4700 | 103 18 15 | |||
| 261 46 20 | 103 17 55 | 92 30 52 | ||
| 261 45 39 | 103 17 35 | |||
| 261 44 59 | 103 17 15 | |||
| 261 44 19 | 103 16 55 | 92 28 51 | ||
| 261 43 39 | 103 16 35 | |||
| 261 42 59 | 103 16 15 | 92 27 30 | ||
| 261 42 18 | 103 15 55 | 92 26 50 | ||
| 261 41 38 | 103 15 35 | 92 26 10 | ||
| 261 40 58 | 103 15 15 | 92 25 30 | ||
| 261 40 19 | 103 14 55 | 92 24 50 | ||
| 261 39 40 | 103 14 35 | 92 24 10 | ||
| 103 14 15 | 92 23 30 | |||
| 261 38 22 | 103 13 55 | 92 22 50 | ||
| 261 37 43 | 103 13 35 | 92 22 09 | ||
| 103 13 15 | 92 21 29 |
Линейная засечка
ХА = + 823,61м; YA= + 192,37м;
Хв = + 329,83м; YB = + 1822,81м;
Хс = + 3138,17м; Y С = +1290,17м;
Принять:
Хр = 2900,10м +1,00м · N (N=1,2,,15)
Yp =-170,20м-1,00м · N
Хр= 2900,20м +1,00м · N (N=1,2,...,15)
Yp = -170,20 м - 1,00м · N
Хр = 2900,30 м +1,00м · N (N=1,2......,15)
Yp = -170,30 м - 1,00м · N
Хр= 2900,40 м +1,00м · N (N=1,2,...,15)
Yp = -170,40м-1,00м · N
Значения S1 ,S2 ,S3 вычислить по формулам: