Развитие понятия о числе

Содержание

Введение……………………………………………………………………….3

1. История возникновения комплексных чисел……………………………..5

1.1 Развитие понятия о числе…………………………………………………5

1.2 На пути к комплексным числам………………………………………….6

1.3 Утверждение комплексных чисел в математике………………………..8

2. Комплексные числа и их свойства…………………………………… ….. 11

2.1 О комплексных числах…………………………………………………..11

2.2 Геометрическое изображение комплексных чисел……………………..12

2.3 Тригонометрическая и показательная формы комплексного числа…...14

3. Действия с комплексными числами………………………………………17

3.1 Сложение комплексных чисел……………………………………………17

3.2 Вычитание комплексных чисел…………………………………………..17

3.3 Произведение комплексных чисел……………………………………….18

3.4 Извлечение корней ………………………………………………………..19

3.5 Геометрический смысл алгебраических операций………………………19

4. Применение комплексных чисел к решению алгебраических уравнений

3-ей и 4-ой степеней………………………………………………………… 22

4.1 Формула Кардано………………………………………………………….22

4.2 Метод Феррари для уравнения 4-ой степени…………………………….23

Заключение……………………………………………………………………..25

Литература……………………………………………………………………..26

Введение

В программе математики школьного курса теория чисел вводится на примерах множеств натуральных чисел, целых, рациональных, иррациональных, т.е. на множестве действительных чисел, изображения которых заполняют всю числовую ось. Но уже в 8 классе запаса действительных чисел не хватает, решая квадратные уравнения при отрицательном дискриминанте. Поэтому было необходимо пополнить запас действительных чисел при помощи комплексных чисел, для которых квадратный корень из отрицательного числа имеет смысл.

Рассмотрев тему «Комплексные числа» на занятиях высшей математики мы заинтересовались данной темой и решили углубить свои познания в этой области.

Выбор темы «Комплексные числа», их прошлое и настоящее» заключается в том, что понятие комплексного числа расширяет знания о числовых системах, о решении широкого класса задач как алгебраического, так и геометрического содержания, о решении алгебраических уравнений любой степени и о решение задач с параметрами.

Большое значение комплексных чисел в математике и её приложениях широко известно. Их изучение имеет самостоятельный интерес. Алгебру комплексных чисел можно успешно использовать в элементарной геометрии, тригонометрии, теории геометрических преобразований, а также в электротехнике и различных задачах с механическим и физическим содержанием.

Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой он является. Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники

Цель настоящего реферата знакомство с историей появления комплексных чисел, их свойствами, действиями над ними, а также с решением уравнений с комплексным переменным.

В рамках достижения поставленной цели были поставлены и решены следующие задачи:

- ввести понятие комплексных чисел и изучить историю их открытия;

- рассмотреть различные свойства и формы комплексных чисел, математические операции с ними;

- использовать изученный материал для решения практических задач в течение учебного года;

- оценить значение и роль комплексных чисел в математике, в повышении интереса в изучении комплексных чисел студентами в развитии их творческих и исследовательских способностей.

История возникновения комплексных чисел

Развитие понятия о числе

Древнегреческие математики считали “настоящими” только натуральные числа. Постепенно складывалось представление о бесконечности множества натуральных чисел.

В III веке Архимед разработал систему обозначения вплоть до такого громадного как 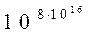. Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил, что “… элементы чисел являются элементами всех вещей и весь мир в челом является гармонией и числом. Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия начинается эра теоретической математики: открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.

Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел - это было сделано китайскими математиками за два века до н. э. Отрицательные числа применяли в III веке древнегреческий математик Диофант, знавший уже правила действия над ними, а в VII веке эти числа уже подробно изучили индийские ученые, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменения величин. Уже в VIII веке было установлено, что квадратный корень из положительного числа имеет два значения - положительное и отрицательное, а из отрицательных чисел квадратный корень извлекать нельзя: нет такого числа 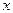, чтобы .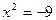