Общая модель сбалансированного роста

Для экономики, описываемой технологическим множеством Z, естественно обобщить введенное в модели Неймана понятие траектории сбалансированного роста (см. определение 5.2).

Траектория 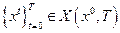называется траекторией сбалансированного роста в экономике, описываемой технологическим множеством , если 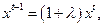где число 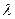есть темп роста. По определению для любых 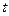и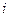

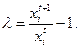
Траекторию сбалансированного роста можно представить в виде где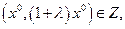

Траектория называется траекторией максимального сбалансированного роста, если 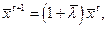где

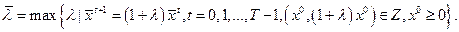
Луч 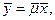порожденный вектором 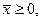удовлетворяющим условию 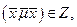где 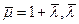- максимальный темп роста, называется лучом максимального сбалансированного роста или неймановским лучом. Заметим, что такой луч, вообще говоря, не является единственным, т.е. для 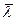могут существовать разные лучи Неймана, порожденные разными

Теорема 6.3. Пусть выполнены следующие условия.

А₁: - замкнутый выпуклый конус в
А₂: Из следует
А₃: Для любого 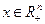существует хотя бы один вектор такой, что 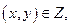т.е. любой мыслимый вектор затрат можно преобразовать в некоторый вектор выпуска. Тогда траектория максимального сбалансированного роста существует.

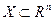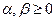
Доказательство. Множество называется выпуклым конусом, если для любых и т.е. конус вместе со своими двумя точками содержит и их любую линейную комбинацию с неотрицательными весами.

Так как при отсутствии затрат темп роста не определен, то для доказательства теоремы рассмотрим полуоткрытую часть : В силу предположения А₃ . Для процесса 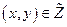темп сбалансированного роста по определению есть

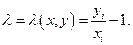(6.2.1)

Требуется доказать существование числа

(6.2.2)

Другими словами, надо установить существование сходящейся последовательности 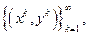такой, что последовательность сходится к 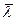и что 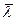- конечное число.

Пронормируем процесс 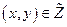следующим образом:

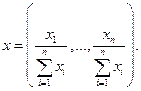
Для нормированного процесса 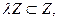очевидно, 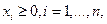и 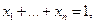т.е. вектор принадлежит стандартному симплексу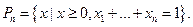

Так как для любого 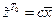по условию А₁ 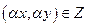и

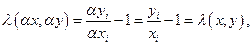
то для определения числа 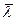можно ограничиться рассмотрением темпов роста для нормированных процессов.

По определению супремума, в найдется (максимизирующая) последовательность 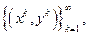такая, что

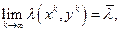
(т.е. последовательность 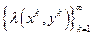сколь угодно близко подходит к числу 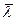). Для такой последовательности обозначим 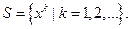Так как для любого 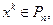то множество 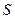ограничено. Последовательность можно представить как сечение множества траекторий 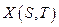в любой фиксированный момент времени (множество является множеством точек, т.е. «однопериодных» процессов 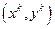). Тогда по лемме 7.1 из ограниченности множества S следует ограниченность множества . При этом из (6.2.1) имеем

(6.2.3)

где 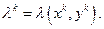Суммируя обе части по i, получаем

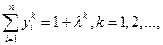
что свидетельствует о конечности чисел .

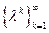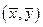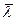Следовательно, последовательности и сходятся соответственно к пределам и , где 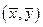- такой процесс, что 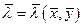. Равенство (6.2.3) в пределе дает 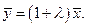Другими словами, максимум в (6.2.2) существует и достигается в точке 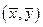, причем ввиду замкнутости Z (согласно условия А₁) имеем Теорема доказана.

Замечание. В литературе встречается доказательство этой теоремы, когда вместо (6.2.1) в качестве темпа роста процесса 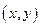рассматривается число

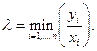(6.2.4)

Тогда вместо (6.2.3) получим 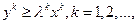что в пределе дает Здесь строгое равенство не получается автоматически. Поэтому следующим шагом доказательства будет установление того, что для некоторых специально подобранных процессов из равенство действительно имеет место. Однако представление (6.2.4) предполагает неравенство отношений 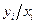для разных 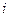, что противоречит определению темпа сбалансированного роста. Это говорит о несостоятельности представления темпа сбалансированного роста в виде (6.2.4). По этой причине мы и исходим из равенства (6.2.1).

Установим некоторые важные для приложений свойства неймановского луча.

Технологическое множество Z называется неразложимым, если существует положительное целое число , такое, что любая допустимая траектория длины 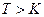обладает следующим свойством: при для каждого 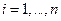найдется такое 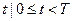что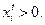

Теорема 6.4. Если технологическое множество неразложимо и то каждый вектор x, порождающий луч Неймана, положителен.

Доказательство. Прежде всего, заметим, что из следует 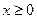, т.е. отрицательные векторы не рассматриваются. Предположим, что для каждого вектора x, порождающего луч Неймана, найдется компонента, равная нулю: Тогда для луча Неймана 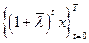для любых 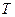и , таких, что 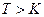, по неразложимости должно быть 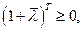а для любых 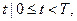из имеем 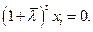Последнее противоречит неразложимости . Теорема доказана.

Пусть 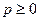- вектор цен. Прибыль от применения процесса без учета временного лага между затратами и выпуском есть а с учетом временного лага Пусть норма процента есть 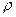. Тогда 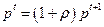(см. определение 5.3) и поэтому в ценах конца периода имеем 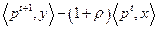или просто 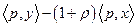(сумма денег, на которую можно приобрести товары в момент 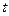, дает возможность купить в момент 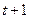в 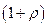раз больше того же товара). Величина называется процентом на капитал.

Выясним существование такого темпа роста 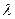, что . В этом случае прибыль от процесс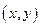а равна 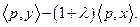Вектор цен , удовлетворяющий условию

(6.2.5)

для любого , называется неймановским вектором цен. Заметим, что здесь не обязан быть порождающим луч Неймана вектором.

Теорема 6.5. Пусть - выпуклое множество, а 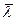- максимальный темп сбалансированного роста. Тогда существует неотрицательный вектор цен Неймана, соответствующий

Если 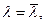а - вектор, порождающий луч максимального сбалансированного роста, то при неймановском векторе цен имеем где 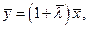т.е. процесс 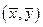максимизирует прибыль (6.2.5).

Если условие (6.2.5) имеет место только для тех векторов x, которые пропорциональны некоторому вектору, порождающему луч Неймана, то говорят, что процесс 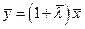исключительно прибыльный.

Теорема 6.6. Если технологическое множество строго выпукло, то при каждом неймановском векторе цен p выполняется условие исключительной прибыльности.

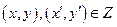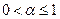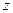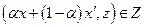В этой теореме строгая выпуклость является усилением свойства выпуклости, сформулированного в разделе 6.1 (второе свойство технологического множества). А именно, множество Z называется строго выпуклым, если для любых и существует такой вектор выпуска , что и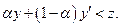

Теорема 6.7. Пусть выполнено условие А₃ из теоремы 7.3 и при любом неймановском векторе цен 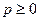имеет место условие исключительной прибыльности. Тогда

1. луч максимального сбалансированного роста единственен;
2. если число продуктов n не меньше двух, то
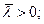
3. не более чем одна компонента вектора может равняться нулю: если i-ая компонента вектора p равна нулю, то все компоненты вектора , за исключением i-ой, равны нулю.

Свойства траектории максимального сбалансированного роста, представленные теоремами 7.4-7.7, помимо практики находят применение в исследовании различных направлений теории экономического роста. Одним из таких направлений является магистральная теория.

Для экономики, описываемой технологическим множеством Z, приведем общую теорему о магистрали Раднера. Эта теорема содержит достаточные условия существования слабой магистрали в оптимизационной задаче (6.1.1). Все необходимые определения о магистрали были приведены в разделе 5.5, там же были сформулированы теоремы о сильных магистралях в динамических оптимизационных задачах Леонтьева и Неймана.

Для формулировки теоремы Раднера нам понадобятся следующие условия.

А₄. Существуют вектор затрат 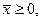вектор цен 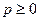и темп роста такие, что 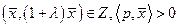и для каждого выполнено неравенство (6.2.5), где для x, не пропорциональных вектору , имеет место строгое неравенство.
А₅. В задаче (6.1.1) 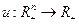(функция 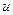неотрицательна), положительно однородна первой степени, т.е. для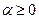 и для всех 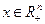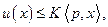где 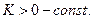Кроме того, существует допустимая траектория (см. раздел 6.1) 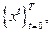такая, что где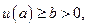
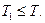
А₆. Для начального состояния 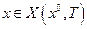существует допустимая траектория 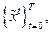такая, что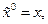 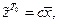где ,

Теорема 6.8 (Раднера). Пусть в экономике, описываемой технологическим множеством , выполнены условия А₁, А₂, А₄-А₆. Тогда для каждого 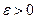существует положительное целое k, такое, что любая оптимальная траектория задачи (6.1.1), исходящая из заданного начального состояния , удовлетворяет условию 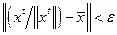всюду на отрезке , за возможным исключением не более чем периодов.

В предположении A₄ является вектором, порождающим луч Неймана, поэтому число 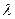является максимальным темпом роста, а p - неймановским вектором цен. Множество 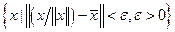называется конической -окрестностью магистрали, порожденной вектором .

Теорема 6.8 дает важную информацию о том, что в условиях выполнения предположений А₁, А₂, А₄-А₆ все оптимальные траектории задачи (6.1.1) на большинстве плановых периодов лежат в конической -окрестности магистрали, представленной (единственным) лучом максимального сбалансированного роста. В то же время эта теорема ничего не говорит о близости оптимальной траектории к магистрали в «средней части» периода и не исключает возможности выхода оптимальной траектории из этой -окрестности на некоторых промежутках времени. По этой причине теорему 6.8 называют слабой теоремой о магистрали, в отличие от сильных теорем о магистрали, приведенных в разделе 5.5 для линейных моделей экономики. Сильная теорема о магистрали в экономике, описываемой технологическим множеством , получается из теоремы 6.8 при некоторых дополнительных условиях.