Модель экономического благосостояния

Анализируя предыдущие разделы, можно прийти к выводу, что одним из важных вопросов, изучаемых в рамках математической экономики, является разработка (моделирование) различных принципов эффективного развития экономики и исследование проблем, с ними связанных. Можно задаться вопросом: зачем надо придумывать все новые и новые постулаты и нормативы, регламентирующие возможные пути протекания экономических процессов? Не лучше ли разработать один всеобъемлющий принцип экономического развития и заниматься его анализом и реализацией?

Причины невозможности разработки одного универсального принципа, которому должны подчиняться экономические процессы, лежат в самой экономике, как сложной, многогранной и противоречивой сфере человеческой деятельности. Чем выше уровень требований к такому принципу, тем сложнее его реализация на практике. Например, можно было бы потребовать, чтобы производители получали максимальные прибыли при минимальных затратах. Но даже на интуитивном уровне понятно, что этот принцип не реализуем ввиду противоречивости его условий. Каждый принцип оптимальности, будь он дискриптивным или нормативным, имеет свои плюсы и свои минусы. Например, принцип конкурентного равновесия хорош тем, что при таком функционировании экономики потребители получают максимальную полезность в рамках имеющихся у них доходов, производители - максимальные прибыли при существующей технологии, а также удовлетворены спросы и предложения всех членов общества на товары. Это - положительная сторона данного принципа. А отрицательная состоит в том, что равновесие может иметь место при очень низком уровне доходов и технологии и в отсутствие качественного и количественного роста экономики, т.е. в условиях застоя. Поэтому хотелось бы, чтобы равновесной траектории экономики были бы присущи и магистральные свойства, вдоль нее были бы соблюдены оптимальные пропорции потребления и инвестиций, экономический прогресс не нарушал бы экологического равновесия и т.д. Однако такое нагромождение требований к экономическому сценарию может привести к невозможности его практической реализации. Поэтому чем больше будет разработано разумных вариантов «оптимального поведения», тем шире будет возможность выбора подходящего для конкретной ситуации, при конкретных сложившихся условиях, сценария развития экономики. Понятно, что каждый такой принцип должен отвечать определенным требованиям адекватности, реалистичности и справедливости (см. раздел 1.7).

Рассмотрим еще один нормативный принцип экономического поведения, который порождает так называемое экономическое благосостояние. Суть экономического благосостояния, в понимании авторов данной концепции, была изложена в начале раздела 6.1. В основе концепции экономического благосостояния лежит принцип оптимальности по Парето (по имени известного итальянского экономиста).

Изначально этот принцип был разработан для задач многокритериальной оптимизации (см. раздел 1.6) вида

(6.4.1)

где - множество допустимых решений единственного ЛПР (лица, принимающего решение), - заданные на множестве X различные целевые функции, описывающие различные цели, преследуемые этим ЛПР. Таким образом, для каждого выбранного ЛПР решения получается n чисел оценивающих качество этого решения.

Допустим, что в существует такая точка , которая максимизирует (или минимизирует) функцию , т.е.

Нет никакой гарантии, что в этой же точке будут достигнуты максимальные (или минимальные) значения остальных функций 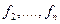ввиду их различности. Поэтому в задачах многокритериальной оптимизации не будут достигнуты максимумы и минимумы всех функций одновременно (за исключением каких-либо тривиальных случаев). Как тогда должен действовать ЛПР, в чем состоит принцип его оптимального поведения и что называть решением задачи многокритериальной оптимизации?

Ответ на эти вопросы получим, если пойдем по пути ослабления требований, определяющих «оптимальное решение». Одним из наиболее распространенных принципов такого рода и является оптимальность по Парето. Он предъявляет к понятию оптимальности более слабые требования, чем максимизация (или минимизация) целевых функций.

Определение 6.1. Точка называется оптимальной по Парето в задаче многокритериальной оптимизации (6.4.1), если не существует другой точки для которой для всех причем хотя бы для одного i имеет место строгое неравенство.

Множество всех оптимальных по Парето точек называется множеством Парето.

Смысл оптимальности точки заключается в том, что переход от нее к любой другой точке (в том числе к другой оптимальной по Парето точке) обязательно сопровождается уменьшением значения хотя бы одной из функций .

Ввиду нежесткости условий, его определяющих, множество Парето почти всегда существует, т.е. непусто.

Пусть - такие неотрицательные числа, что Для любой точки выпуклая комбинация

(6.4.2)

называется сверткой критериев в задаче (6.4.1).

Следующая теорема дает признак оптимальности по Парето.

Теорема 6.9. Пусть в задаче многокритериальной оптимизации (6.4.1) множество X замкнуто и выпукло, а все функции вогнуты. Тогда

если все коэффициенты в (6.4.2) положительны, то вектор , максимизирующий свертку критериев (6.4.2) на множестве , оптимален по Парето;
обратно, для любой оптимальной по Парето в задаче (6.4.1) точки существуют неотрицательные и не все равные нулю числа , такие, что свертка критериев (6.4.2) достигает максимального значения в точке .

Исходя из того факта, что оптимальность по Парето формализует один из принципов «социальной справедливости», желательно, чтобы равновесные векторы потребления удовлетворяли этому принципу оптимальности. В теории экономического благосостояния оптимальность по Парето изучается наряду с концепцией конкурентного равновесия. Мы хотим получить ответ на вопрос: будут ли оптимальными по Парето векторы потребления, входящие в состояние равновесия (в смысле Вальраса)?

Для доказательства соответствующих теорем возьмем за основу модель Эрроу-Дебре, существование равновесия в которой было доказано в разделе 4.4 (теорема 3.2). Поэтому далее будем пользоваться обозначениями разделе 4.4 и будем предполагать выполненными условия (У-1)-(У-6).

Совместным распределением потребления и производства или просто распределением в модели Эрроу-Дебре будем называть пару удовлетворяющую условиям

(6.4.3)

где - множество допустимых векторов потребления i -го потребителя, - множество производственных планов j -го производителя, - вектор начальных запасов товаров для i -го потребителя. Обозначим

Согласно определения 6.1, распределение назовем оптимальным по Парето распределением, если не существует распределения для которого причем хотя бы для одного потребителя имеет место строгое неравенство, где - функция полезности потребителя 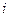(см. (4.4.2)).

Множество Парето-оптимальных распределений можно охарактеризовать как множество коллективно предпочитаемых наборов благ, так как область поиска окончательного распределения от множества сужается до множества Парето.

Следующее утверждение показывает, что оптимальность по Парето является одним из признаков конкурентного равновесия.

Теорема 6.10. Если - конкурентное равновесие в модели Эрроу-Дебре, то распределение оптимально по Парето.

Доказательство. Тот факт, что является распределением, следует из соотношений (4.3.9)-(4.3.11).

Предположим, что распределение не является оптимальным по Парето. Тогда найдется такая пара что и хотя бы одно из этих неравенств строгое.

Из условия У-5 (см. раздел 4.4) следует существование такого элемента что Составим выпуклую комбинацию Поскольку выпукло (см. У-3), то , а из вогнутости функции (см. У-4) следует 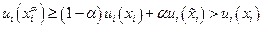при Отсюда получаем

(6.4.4)

Так как - решение оптимизационной задачи i -го потребителя, то является максимальным значением функции на бюджетном множестве i -го потребителя, а сама точка лежит на бюджетной линии

Поэтому из (6.4.4) следует

(6.4.5)

Легко видеть, что

Поэтому из (6.4.5) следует

где, исходя из нашего предположения, хотя бы для одного i выполняется строгое неравенство. Суммируя обе части этого неравенства по получаем

(6.4.6)

Так как - решение оптимизационной задачи производителя, то

для всех Тогда из (6.4.6) получаем

(6.4.7)

Если умножить обе части неравенства (6.4.3), определяющего распределение , то получим неравенство, противоположное к (6.4.6). Это противоречие опровергает наше предположение о том, что распределение не является оптимальным по Парето. Теорема доказана.

Следующее утверждение показывает, что оптимальность по Парето распределения является «почти» достаточным условием существования конкурентного равновесия для некоторого вектора цен

Теорема 6.11. С каждым оптимальным по Парето распределением в модели Эрроу-Дебре можно связать вектор цен такой, что

a) вектор максимизирует на множестве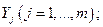
b) вектор минимизирует на множестве

Доказательство. Докажем утверждение a). Введем в рассмотрение вспомогательное множество

где Нетрудно видеть, что множество (см. утверждение b) теоремы) является замыканием . Из условия У-5 следует

Любой элемент выглядит так

(6.4.8)

Поэтому для любого распределения (см. (6.4.3)).

Благодаря условиям У-3 и У-4, все и, следовательно, являются выпуклыми множествами. Применяя лемму 4.2 для выпуклых множеств и , получаем, что существует такой вектор , для которого для любых Подставляя сюда выражение 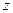из (6.4.8), получаем

(6.4.9)

Это же неравенство получается, если в определении множества вместо взять Действительно, составим вектор где Из вогнутости следует и потому неравенство (6.4.9) остается справедливым при замене всех на :