Варианты
0. 
1. 
. 
.
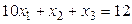
2. 
.
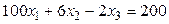
3. 
4. 
.
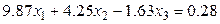
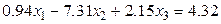
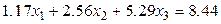5. 
6. 
7. 
8. 
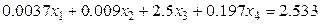
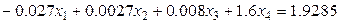
9. 
2. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИИ МНОГОЧЛЕНОМ ЛАГРАНЖА
Постановка задачи. Пусть величина у является функцией аргумента х. Это означает, что любому значению х из области определения поставлено в соответствие значение у. Вместе с тем на практике часто неизвестна явная связь между у и х, т.е. невозможно записать эту связь в виде некоторой зависимости 
. В некоторых случаях даже при известной зависимости она настолько громоздка (например, содержит трудно вычисляемые выражения, сложные интегралы и т.д.), что её использование в практических расчетах затруднительно.
Наиболее распространенным и практически важным случаем, когда вид связи между параметрами х и у неизвестен, является задание этой связи в виде некоторой таблицы 
. Это означает, что дискретному множеству значений аргумента 
поставлено в соответствие множество значений функции 
Эти значения - либо результаты расчетов, либо экспериментальные данные. На практике нам могут понадобиться значения величины у и в других точках, отличных от узлов 
. Таким образом, необходимо использовать имеющиеся табличные данные для приближенного вычисления искомого параметра 
при любом значении (из некоторой области) определяющего параметра 
, поскольку точная связь 
неизвестна.
Этой цели и служит задача о приближении (аппроксимации) функций: данную функцию 
требуется приближенно заменить (аппроксимировать) некоторой функцией 
так, чтобы отклонение (в некотором смысле) от в заданной области было наименьшим. Функция при этом называется аппроксимирующей.
Для практики весьма важен случай аппроксимации функции многочленом
|
|
(4)
При этом коэффициенты 
будут подбираться так, чтобы достичь наименьшего отклонения многочлена от данной функции.
Одним из основных типов аппроксимации является интерполирование. Оно состоит в следующем: для данной функции строим многочлен (4), принимающий в заданных точках 
те же значения 
что и функция , т.е.
(5)
При этом предполагается, что среди значений 
нет одинаковых, т.е. 
при 
Точки называются узлами интерполяции, а многочлен 
- интерполяционным многочленом.
Пусть функция определена таблицей
|
| 
| 
| … | 
|
|
| 
| 
| … | 
|
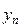
Задачей интерполяции является построение многочлена 
, значения которого в узлах интерполяции { xi } равны соответствующим значениям заданной функции, т.е.
=yi (i =0,1,…, n).
Интерполяционной формулой Лагранжа называется формула, представляющая многочлен в виде
, (6)
где 
- многочлен степени n, принимающий значение, равное единице в узле 
, и равные нулю значения в остальных узлах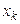 
( 
), (i,k =0,1,…, n). Многочлен называется интерполяционным многочленом Лагранжа. Следует отметить, что степень многочлена Лагранжа не превышает числа n. определяется по следующей формуле
. (7)
Пример. Для функции, заданной таблицей, построить интерполяционный многочлен Лагранжа.
|
| -1 | ||
|
|
Решение. Многочлен Лагранжа для трех узлов интерполирования запишется так:
Применяя формулу Лагранжа, получим
После элементарных преобразований получаем интерполяционный многочлен Лагранжа второй степени 
.
Задание 2
|
|
Для функции ,заданной таблицей, построить интерполяционный многочлен Лагранжа.
Варианты
0.
|
| 2.5 | 3.0 | 3.5 | 4.0 |
|
| 1.4981 | 1.4675 | 1.4323 | 1.3931 |
1.
|
| 0.0 | 0.5 | 1.0 | 1.5 | 2.0 |
|
| 1.5708 | 1.5738 | 1.5828 | 1.5981 | 1.62 |
2.
|
| 2.5 | 3.0 | 3.5 | 4.0 |
|
| 1.649 | 1.6858 | 1.7313 | 1.7868 |
3.
|
| 0.3 | 0.4 | 0.50 | 0.6 | 0.7 |
|
| 0.29131 | 0.37995 | 0.46212 | 0.53705 | 0.60437 |
4.
|
| 0.8 | 0.9 | 1.0 |
|
| 0.66404 | 0.7163 | 0.76159 |
5.
|
| 0.0 | 0.5 | 1.0 | 1.05 | 2.0 |
|
| 1.5708 | 1.5678 | 1.5589 | 1.5442 | 1.5238 |
6.
|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
|
| 0.11246 | 0.2227 | 0.32863 | 0.42839 | 0.5205 |
7.
|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
|
| 0.17469 | 0.35031 | 0.52773 | 0.70765 | 0.89054 |
8.
|
| 0.1 | 0.2 | 0.3 | 0.4 |
|
| 1.07657 | 1.26548 | 1. 45663 | 1.649 |
9.
|
| 0.60 | 0.65 | 0.70 | 0.75 | 0.80 |
|
| 0.912 | 0.897 | 0.881 | 0.864 | 0.846 |