Постановка задачи. Пусть на отрезке  задана функция
задана функция  . С помощью точек
. С помощью точек 
 …,
…,  разобьем отрезок
разобьем отрезок  на n отрезков
на n отрезков  (
( ), причем
), причем 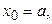
 . На каждом их этих отрезков выберем произвольную
. На каждом их этих отрезков выберем произвольную 
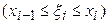 и найдем произведение
и найдем произведение  значения функции в этой точке
значения функции в этой точке 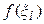 на длину отрезка
на длину отрезка  :
:
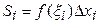 (19)
(19)
Составим сумму всех таких произведений:
 (20)
(20)
Сумма  называется интегральной суммой. Определенным интегралом от функции
называется интегральной суммой. Определенным интегралом от функции  на отрезке [ a,b ] называется предел интегральной суммы при неограниченном увеличении числа точек разбиения; при этом длина наибольшего из отрезков стремится к нулю:
на отрезке [ a,b ] называется предел интегральной суммы при неограниченном увеличении числа точек разбиения; при этом длина наибольшего из отрезков стремится к нулю:
 (21)
(21)
Теорема существования определенного интеграла. Если функция  непрерывна на отрезке [ a,b ], то предел интегральной суммы существует и не зависит ни от способа разбиения отрезка [ a,b ], ни от выбора точек
непрерывна на отрезке [ a,b ], то предел интегральной суммы существует и не зависит ни от способа разбиения отрезка [ a,b ], ни от выбора точек  .
.
 Геометрический смысл введенных понятий для случая
Геометрический смысл введенных понятий для случая  >0 проиллюстрирован на рис. 2.
>0 проиллюстрирован на рис. 2.
Рис. 2
Абсциссами точек  являются значения
являются значения 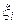 , ординатами – значения
, ординатами – значения  . Выражения (19) при
. Выражения (19) при  описывают площади элементарных прямоугольников (штриховые линии), интегральная сумма (20) - площадь ступенчатой фигуры, образуемой этими прямоугольниками. При неограниченном увеличении числа точек деления и стремлении к нулю всех
описывают площади элементарных прямоугольников (штриховые линии), интегральная сумма (20) - площадь ступенчатой фигуры, образуемой этими прямоугольниками. При неограниченном увеличении числа точек деления и стремлении к нулю всех  верхняя граница фигуры (ломаная) переходит в линию
верхняя граница фигуры (ломаная) переходит в линию  . Площадь полученной фигуры, которую называют криволинейной трапецией, равна определенному интегралу (21).
. Площадь полученной фигуры, которую называют криволинейной трапецией, равна определенному интегралу (21).
Во многих случаях, когда подынтегральная функция задана в аналитическом виде, определенный интеграл удается вычислить непосредственно с помощью неопределенного интеграла (вернее, первообразной) по формуле Ньютона-Лейбница. Она состоит в том, что определенный интеграл равен приращению первообразной  на отрезке интегрирования:
на отрезке интегрирования:
 . (22)
. (22)
Однако на практике этой формулой часто нельзя воспользоваться по двум основным причинам:
1) вид функции  не допускает непосредственного интегрирования, т.е. первообразную нельзя выразить в элементарных функциях;
не допускает непосредственного интегрирования, т.е. первообразную нельзя выразить в элементарных функциях;
2) значения функции  заданы только на фиксированном конечном множестве точек
заданы только на фиксированном конечном множестве точек  , т.е. функция задана в виде таблицы.
, т.е. функция задана в виде таблицы.
В этих случаях используют методы численного интегрирования. Они основаны на аппроксимации подынтегральной функции некоторыми более простыми выражениями, например, многочленами.
Методы прямоугольников и трапеций
Простейшим методом численного интегрирования является метод прямоугольников. Он непосредственно использует замену определенного интеграла интегральной сумой (20). В качестве точек  могут выбираться левые (
могут выбираться левые ( ) или правые (
) или правые (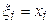 ) границы отрезков. Обозначая
) границы отрезков. Обозначая  ,
, 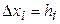 , получаем следующие формулы метода прямоугольников соответственно для этих двух случаев:
, получаем следующие формулы метода прямоугольников соответственно для этих двух случаев:
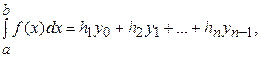 (23)
(23)
 (24)
(24)
Более точным является вид формулы прямоугольников, использующий значения функции в средних точках отрезков (в полуцелых узлах):
 , (25)
, (25)
 ,
,  .
.
В дальнейшем под методом прямоугольников будем понимать последний алгоритм (он еще называется методом средних).
Метод трапеций использует линейную интерполяцию, т.е. график функции  представляется в виде ломаной, соединяющий точки
представляется в виде ломаной, соединяющий точки 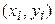 . В этом случае площадь всей фигуры (криволинейной трапеции) складывается из площадей прямолинейных трапеций (рис. 3).
. В этом случае площадь всей фигуры (криволинейной трапеции) складывается из площадей прямолинейных трапеций (рис. 3).
Площадь каждой такой трапеции равна произведению полусуммы оснований на высоту:

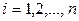 .
.
Складывая все эти равенства, получаем формулу трапеций для численного интегрирования:
 . (26)
. (26)


Рис. 3
Важным частным случаем этих формул является их применение при численном интегрировании с постоянным шагом  (
( . Формулы прямоугольников и трапеций в этом случае принимают соответственно вид:
. Формулы прямоугольников и трапеций в этом случае принимают соответственно вид:
 (27)
(27)
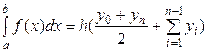 . (28)
. (28)
Метод Симпсона
Разобьем отрезок интегрирования [ a,b ] на четное число n равных частей с шагом h. На каждом отрезке 
 …,
…,  , …,
, …, 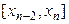 подынтегральную функцию
подынтегральную функцию  заменим интерполяционным многочленом второй степени:
заменим интерполяционным многочленом второй степени:
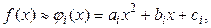
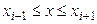 .
.
Коэффициенты этих квадратных трехчленов могут быть найдены из условий равенства многочлена в точках  соответствующим табличным данным
соответствующим табличным данным  . В качестве
. В качестве  можно принять интерполяционный многочлен Лагранжа второй степени, проходящий через точки
можно принять интерполяционный многочлен Лагранжа второй степени, проходящий через точки  ,
,  ,
,  :
:

 .
.
Элементарная площадь  (рис. 4) может быть вычислена с помощью определенного интеграла.
(рис. 4) может быть вычислена с помощью определенного интеграла.
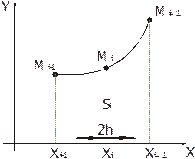
Рис. 4
Учитывая равенства 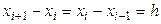 , получаем
, получаем


Проведя такие вычисления для каждого отрезка 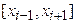 , просуммируем полученные выражения:
, просуммируем полученные выражения:
 .
.
Данное выражение для S принимается в качестве значения определенного интеграла:

 (29)
(29)
Полученное соотношение (29) называется формулой Симпсона.
Пример. Вычислить интеграл  методами прямоугольников, трапеций и Симпсона.
методами прямоугольников, трапеций и Симпсона.
Решение. Используем для вычисления интеграла формулы прямоугольников и трапеций. Для этого разобьем отрезок интегрирования [0,1] на десять равных частей: n= 10, h =0.1. Вычислим значения подынтегральной функции  в точках разбиения
в точках разбиения  , а также в полуцелых точках
, а также в полуцелых точках  ,
,  . Результаты вычислений занесем в таблицу 4.
. Результаты вычислений занесем в таблицу 4.
Таблица 4

| 
| 
| 
|
| 0.0 | 1.000000 | - | - |
| 0.1 | 0.990099 | 0.05 | 0.997506 |
| 0.2 | 0.961538 | 0.15 | 0.977995 |
| 0.3 | 0.917431 | 0.25 | 0.941176 |
| 0.4 | 0.862069 | 0.35 | 0.890868 |
| 0.5 | 0.800000 | 0.45 | 0.831601 |
| 0.6 | 0.735294 | 0.55 | 0.767754 |
| 0.7 | 0.671141 | 0.65 | 0.702988 |
| 0.8 | 0.609756 | 0.75 | 0.640000 |
| 0.9 | 0.552486 | 0.85 | 0.580552 |
| 1.0 | 0.500000 | 0.95 | 0.525624 |
По формуле прямоугольников (27) получим 
 .
.
Вычислить значение интеграла по методу Симпсона. Значения функции при n= 10, h =0.1 приведены в таблице 1. Применяя формулу (29), находим:

 .
.
Задание 5
Вычислить интеграл методами прямоугольников, трапеций и Симпсона.
Варианты
0.  1.
1.  2.
2. 
3.  4.
4.  5.
5. 
6. 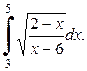 7.
7.  8.
8. 
9. 