(проволочные потенциометры)
Эти датчики используются в автоматике для преобразования перемещений в электрическое напряжение и представляют из себя реостаты с ползунком, включаемые по схемам, соответствующим потенциометрическому методу измерений. В электроавтоматике используются нереверсивная (рис. 1.2) и реверсивная (рис.1.3) схемы включения потенциометров.
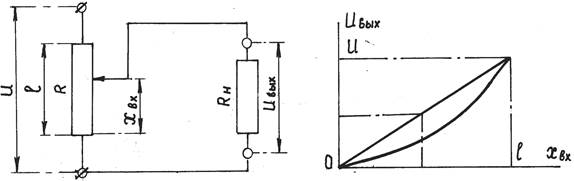
а) б)
Рис.1.2. Нереверсивная схема включения
Представленная на рис. 1.2 схема является нереверсивной, так как при любом положении ползунка знак Uвых и его фаза не меняются. Статическая характеристика такой схемы Uвых = f(x вх) (рис. 1.2, б) в общем виде является нелинейной и становится линейной только при условии, что Rн>>r0, где r0 – сопротивление самого потенциометра. При несоблюдении этого условия будет сказываться шунтирующее действие нагрузки Rн, что и сказывается на характере нелинейности статической характеристики схемы. Так как эта кривая всегда имеет плавный вид, то поэтому потенциометрические устройства и относятся к категории датчиков. При активной нагрузке потенциометр практически безынерционен, т.е.:
Uвых = k · xвх . (1.1)
Переходные процессы в данной схеме будут иметь место только при значительной емкости или индуктивности нагрузки.
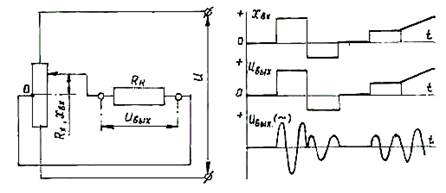
Рис. 1.3. Реверсивная схема включения потенциометра
На рис. 1.3 показана реверсивная схема со вторым (постоянным) контактом с витками потенциометра. Эта схема дает линейную статическую характеристику, малозависящую от величины нагрузки, и позволяет обеспечить более высокий к.п.д. Достоинства такой схемы заключаются в конструктивной простоте, в небольших габаритах и весе датчика, а также в возможности питания схемы как постоянным, так и переменным током. В случае питания переменным током перемещению пропорциональна величина огибающей Uвых, а изменение знака перемещения, то есть знака отклонения положения ползунка относительно его нулевого положения сопровождается изменением фазы Uвых на 180˚ (рис. 3.1).
Построим статическую характеристику Uвых = f(x вх) для данной схемы. Полагаем, что потенциометр является линейным, то есть его витки имеют одинаковую длину. При x вх = (x вх)max = L / 2 и при условии Rн>>r0 получим:
Uвых = (U / L) ∙ x вх. (1.2)
Эта зависимость представляет из себя прямую, проведенную из начала координат под углом β = arctg (U / L).
Полученное выражение для статической характеристики дает точные результаты уже при Rн > (8…10)r0.
В процессе эксплуатации датчиков возможен нагрев их контактных поверхностей. Желательно, чтобы температура не превышала 200 ˚С, так как при больших температурах начинается интенсивное окисление конструкционных материалов.
В датчиках желательно использовать проволоку меньшего диаметра. Это необходимо как для снижения уровня “шумов” в САУ, так и для уменьшения размеров датчика.
Емкостные датчики
Эти датчики относятся к преобразователям параметрического типа. Принцип их действия основан на изменении емкости конденсатора при воздействии входной величины. Основными параметрами и характеристиками емкостных датчиков являются:
- начальная емкость С0;
- реактивное x c = 1 / ωC и активное Rc сопротивления;
- тангенс угла диэлектрических потерь tg δ;
- постоянная времени T = Rc ∙ C0;
- максимальное изменение емкости, чувствительность, статическая и динамическая характеристики.
Для плоских конденсаторов величина емкости зависит от площади электродов (S), расстояния между ними (d) и диэлектрической проницаемости среды (ε). Емкостные датчики выпускаются трех типов со статическими характеристиками, изображенными на рис. 1.4:
∆C = φ(S), ∆C = φ(d) и ∆C = φ(ε). (1.3)
Такие датчики применяют для преобразования линейных и угловых перемещений.

а) б) в)
Рис. 1.4. Датчики с переменной площадью электродов
Для плоского конденсатора (рис. 1.4, а):
∆C = ε ∙ b ∙ ∆l / d, (1.4)
где b – ширина электрода.
Для цилиндрического конденсатора (рис. 1.4, б):
С = 2π · ε ·∆l / ln (d2 / d1). (1.5)
Емкость датчиков поворотного типа (рис. 1.4, в) линейно зависит от угла поворота φ:
C = ε · S (1 – φ / π) / d. (1.6)
Емкостные датчики с изменяющимся зазором (d) (рис. 1.5) в общем случае имеют нелинейную статическую характеристику C = φ (∆d).
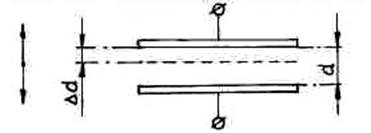
Рис. 1.5. Датчик с изменяющимся расстоянием между электродами
При малых перемещениях (∆d << d) изменение емкости конденсатора:
C = ε · S ·∆d / d², (1.7)
а статическая характеристика будет линейной. Датчики такого типа обладают большой чувствительностью и используются для контроля очень малых перемещений (от 0 до 1 мм). Датчики с изменяющейся площадью электродов применяются для измерения перемещений больших 1 мм.
Емкостные датчики с изменяющейся диэлектрической проницаемостью (рис. 1.6, а и б) применяют для контроля уровня, состава и концентрации жидких, а также толщины и влажности твердых диэлектриков.
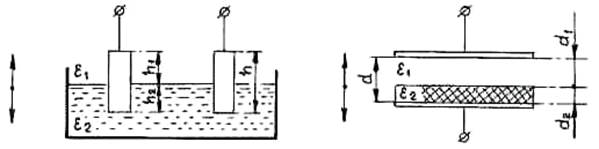
а) б)
Рис. 1.6. Датчики с изменяющейся диэлектрической проницаемостью
Датчик для измерения уровня жидкости (рис. 1.6, а) представляет собой сложный конденсатор, общая емкость которого равна емкости 2–х параллельно включенных конденсаторов:
C = (ε1· b· h / d) + (ε2 – ε1)· b· h2 / d. (1.8)
Емкость такого конденсатора линейно зависит от h2, по величине которой и контролируют уровень жидкости.
Конденсатор с 2 – слойным диэлектриком (рис. 1.6, б) представляет собой два последовательно включенных конденсатора, эквивалентная емкость которых:
C = S / (d1 / ε1+d2 / ε2). (1.9)
Большие отклонения емкости проверяются довольно просто. Для измерения малых отклонений емкости датчики включают в резонансные, мостовые и т.д. схемы. Для увеличения чувствительности емкостных датчиков используют источники питания высокой (свыше 400 Гц) частоты.
Одной из схем включения емкостных датчиков (дифференциальных емкостных преобразователей) является емкостно – диодная цепь (рис. 1.7).
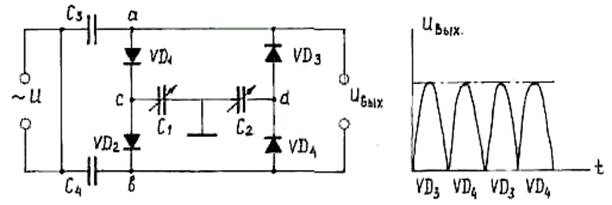
Рис. 1.7. Емкостно – диодная цепь
При положительной полярности U конденсатор С1 заряжается через С3 и VD1, а при отрицательной – разряжается через С4 и VD2 . Конденсаторы С3 и С4 имеют равные емкости, а диоды VD1 и VD2 - равные прямые сопротивления. Если все диоды имеют одинаковые прямые сопротивления, то при С1 = С2 напряжение между точками c и d отсутствует. Если же С1 ≠ С2 , то между точками c и d появится переменное напряжение пропорциональное разности С1 – С2 . Это напряжение выпрямляется в течение одного полупериода диодами VD1 и VD3, а в течение второго – диодами VD2 и VD4. Выходное напряжение снимается с диодов VD3 и VD4. Среднее выпрямленное напряжение Uвых определяется разностью С1 – С2 и приближенно равно:
Uвых = 2U ~ (C1 – С2) / (С1 + С2 + 2С1С2 / C3). (1.10)
Достоинством емкостных датчиков являются простота конструкции, высокая чувствительность, малая инерционность, небольшие габариты и масса.
Индуктивные датчики
Принцип работы этих датчиков основан на изменении индуктивности катушки с магнитопроводом под воздействием различных факторов. Датчики применяются при преобразовании линейных и угловых перемещений, при контроле изменения давления, расходов жидкостей и газов. Индуктивность L катушки с магнитопроводом при наличии воздушного зазора δ равна:
L = w2 / [lм / (μSм) + 2δ / (μ0 Sδ)], (1.11)
где w - число витков катушки;
lм – средняя длина стального магнитопровода;
δ - длина воздушного зазора;
Sм – площадь поперечного сечения стального магнитопровода;
Sδ - площадь поперечного сечения воздушного зазора;
Согласно данному соотношению индуктивные датчики можно построить на использовании изменения величин зазора и его площади или магнитной проницаемости (магнитоупругие датчики).
Простейший индуктивный датчик линейного перемещения с переменной величиной воздушного зазора δ представлен на рис. 1.8.
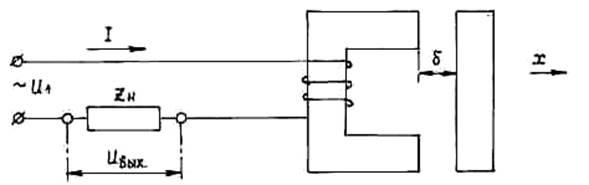
Рис. 1.8. Датчик с переменной величиной воздушного зазора
В этом датчике изменения величины воздушного зазора δ приводит к изменению индуктивности катушки L. Магнитное сопротивление цепи определяется сопротивлениями Rм.ст. двух воздушных зазоров Rδ, т.е. Rм = Rм.ст. + Rδ, где
Rм.ст. = lм / μSм – магнитное сопротивление магнитопровода;
Rδ = 2 δ / μ0 Sδ – магнитное сопротивление воздушного зазора.
Но, так как Rδ >> Rм.ст. , то:
L ≈ w² / Rδ = μ0 · w² · S / (2δ), (1.12)
т.е. индуктивность катушки обратно пропорциональна величине воздушного зазора. Если принять Rк и х к = ω · L – активное и индуктивное сопротивление катушки, а Rн и x н - активное и индуктивное сопротивление нагрузки.
Обычно х к >> Rк, а сопротивление нагрузки мало по сравнению с сопротивлением катушки, откуда напряжение на выходе датчика:
Uвых ≈ 2 U1 · Rн · δ / (ω · w² · μ0 · S) = kδ. (1.13)
При принятых допущениях статическая характеристика Uвых = φ(δ) индуктивного датчика будет линейной. Отклонение ξ характеристики от линейного закона возможны при малых δ (влияние сопротивления Rм.ст.) и при больших δ (возрастают потоки рассеяния).
Индуктивные датчики с переменной величиной воздушного зазора применяют для измерения перемещений порядка 0…1 мм, для измерения перемещений 5...8 мм применяют индуктивные датчики с переменной площадью, а для измерения перемещений до 50 мм – индуктивные датчики плужерного типа. Все эти датчики являются слабочувствительными при малых перемещениях и однотактными, т.е. нереагирующими на изменения знака входной величины.
Отмеченные недостатки отсутствуют у двухтактных (реверсивных) индуктивных датчиков, обычно включаемых по дифференциальной или мостовой схемам (рис. 1.9).
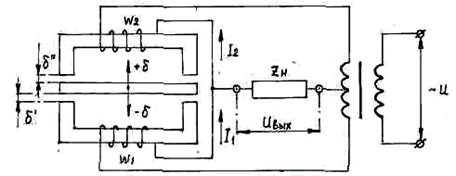
Рис. 1.9. Двухтактный индуктивный датчик
Изображенный дифференциальный индуктивный датчик (ДИД) при среднем положении якоря (δ' = δ'') обеспечивает одинаковую индуктивность катушек, что дает равенство тока в катушках (I1 = I2) и равенство нулю выходного напряжения:
Jвых. = (I1 – I2) Zн = 0. (1.14)
Перемещения якоря в любую из сторон соответствующим образом изменяет индуктивность катушек, приводит к неравенству тока в катушках и к появлению напряжения на выходе.
Дифференциально – трансформаторные датчики применяют для измерения малых перемещений. Индуктивные датчики являются безынерционными элементами автоматики при условии, что частота входного сигнала изменяется во много раз медленнее по сравнению с частотой источника питания.