Устойчивость АРРМ.
АРРМ (5.68) является устойчивой, если устойчивой оказывается соответствующая ей АРМ [14, 26]. АРРМ представляют собой неоднородное разностное уравнение. Для анализа ее устойчивости запишем соответствующее однородное разностное уравнение (АРМ):
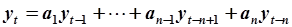
| (5.76) |
или
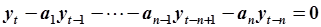 . .
|
Выполним подстановку 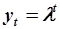 , придем к уравнению
, придем к уравнению
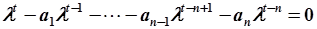
| |
| или | |
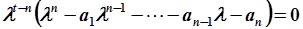 . .
|
Так как 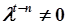 при любых
при любых 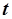 и
и 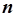 , последнее уравнение можно записать в виде
, последнее уравнение можно записать в виде
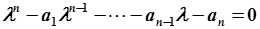 . .
| (5.77) |
Полученное уравнение называется характеристическим уравнением (для исходного разностного уравнения (5.76)).
Для того чтобы АРРМ была устойчивой, необходимо и достаточно, чтобы все корни характеристического полинома по модулю были меньше единицы (располагались внутри единичной окружности на комплексной плоскости).
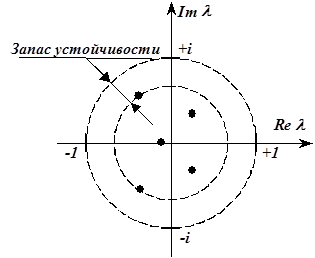 Рис. 5.11. Корни характеристического полинома на комплексной плоскости.
Рис. 5.11. Корни характеристического полинома на комплексной плоскости.
| Величину 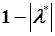 (где (где  - максимальный по модулю корень) называют запасом устойчивости. Чем больше эта величина, тем быстрее сходится АРРМ к некоторому установившемуся значению (при постоянном входном воздействии). На рис.5.11 точками изображены корни характеристического полинома, максимально удаленный от начала координат корень определяет запас устойчивости АРРМ. - максимальный по модулю корень) называют запасом устойчивости. Чем больше эта величина, тем быстрее сходится АРРМ к некоторому установившемуся значению (при постоянном входном воздействии). На рис.5.11 точками изображены корни характеристического полинома, максимально удаленный от начала координат корень определяет запас устойчивости АРРМ.
|
Пример. Рассмотрим АРРМ вида
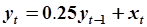 . .
| (5.78) |
Однородное разностное уравнение имеет вид 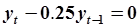 . Характеристическое уравнение
. Характеристическое уравнение 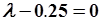 , его решение
, его решение 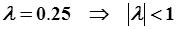 , АРРМ устойчива, запас устойчивости
, АРРМ устойчива, запас устойчивости 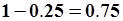 .
.
Пример. Рассмотрим аналог второго закона Ньютона (5.70). Параметры модели 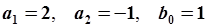 , Однородное разностное уравнение имеет вид
, Однородное разностное уравнение имеет вид 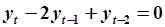 , характеристическое уравнение
, характеристическое уравнение  . Корни характеристического полинома
. Корни характеристического полинома 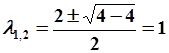 ,
, 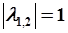 , система не устойчива, запас устойчивости равен нулю.
, система не устойчива, запас устойчивости равен нулю.
Установившийся режим.
Предположим, что входное воздействие постоянно: 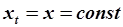 . В установившемся режиме выходной процесс
. В установившемся режиме выходной процесс 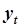 является неизменным (постоянным во времени). Поэтому в (5.68) можно
является неизменным (постоянным во времени). Поэтому в (5.68) можно 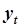 заменить на некоторую (подлежащую определению) постоянную
заменить на некоторую (подлежащую определению) постоянную 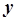 . В этом случае АРРМ (5.68) примет вид:
. В этом случае АРРМ (5.68) примет вид:
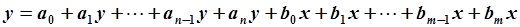
|
где 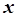 - заданная постоянная. Разрешая последнее уравнение относительно
- заданная постоянная. Разрешая последнее уравнение относительно 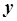 , получим установившееся значение выходной переменной:
, получим установившееся значение выходной переменной:
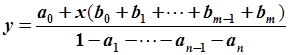 . .
| (5.79) |
Так как установившееся значение рассматривается при 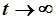 , вклад начальных условий для устойчивых АРРМ отсутствует и, следовательно, установившееся значение от начальных условий не зависит.
, вклад начальных условий для устойчивых АРРМ отсутствует и, следовательно, установившееся значение от начальных условий не зависит.
Установившееся значение по (5.79) может быть получено как для устойчивых, так и неустойчивых АРРМ. В случае неустойчивой АРРМ установившееся значение (равновесие) оказывается неустойчивым и не может быть реализовано при произвольных начальных условиях. Начальные условия при этом могут быть вычислены следующим образом:
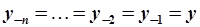 . .
| (5.80) |
Пример. Рассмотрим АРРМ вида (5.78). Данная модель устойчива.
Установившийся режим. Пусть входное воздействие постоянно и задано: 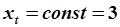 . Для данной АРРМ уравнение (5.79) примет вид:
. Для данной АРРМ уравнение (5.79) примет вид:
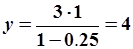 . .
|
На рис. 5.12 приводятся траектории движения системы (5.78) при 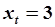 и различных начальных условиях
и различных начальных условиях 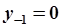 и
и 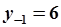 .
.
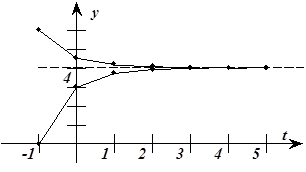 Рис. 5.12. траектории движения системы (5.78).
Рис. 5.12. траектории движения системы (5.78).
| t | yt | t | yt | |
| -1 | -1 | ||||
| 3,000 | 4,500 | ||||
| 3,750 | 4,125 | ||||
| 3,938 | 4,031 | ||||
| 3,984 | 4,008 | ||||
| 3,996 | 4,002 | ||||
Пример. Рассмотрим неустойчивую систему:
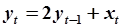 . .
| (5.81) |
Однородное разностное уравнение имеет вид 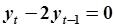 , характеристическое уравнение
, характеристическое уравнение 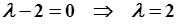 , система неустойчива.
, система неустойчива.
Рассмотрим равновесное состояние неустойчивой системы. Пусть 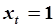 . Запишем (5.79) для (5.81):
. Запишем (5.79) для (5.81): 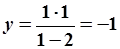 точка неустойчивого равновесия, в соответствии с (5.80), реализуется при начальных условиях
точка неустойчивого равновесия, в соответствии с (5.80), реализуется при начальных условиях 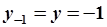 .
.
Пример. Рассмотрим аналог колебательного звена с затуханием (5.72). Параметры модели 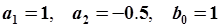 , начальные условия нулевые:
, начальные условия нулевые: 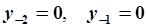 , входное воздействие постоянное:
, входное воздействие постоянное: 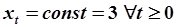 . Траектория движения представлена на рис.5.13.
. Траектория движения представлена на рис.5.13.
Анализ устойчивости. Однородное разностное уравнение имеет вид 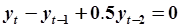 , характеристическое уравнение
, характеристическое уравнение 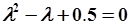 , Корни характеристического полинома
, Корни характеристического полинома
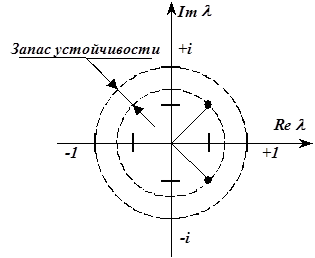 Рис. 5.13. Корни характеристического полинома на комплексной плоскости.
Рис. 5.13. Корни характеристического полинома на комплексной плоскости.
| 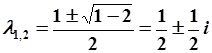
 , система устойчива. Запас устойчивости , система устойчива. Запас устойчивости 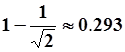 .
Установившийся режим. Входное воздействие постоянно и задано: .
Установившийся режим. Входное воздействие постоянно и задано: 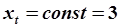 . Для данной АРРМ уравнение (5.79) примет вид: . Для данной АРРМ уравнение (5.79) примет вид:
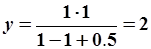 На рис. 5.14 представлена траектория движения системы
На рис. 5.14 представлена траектория движения системы
|
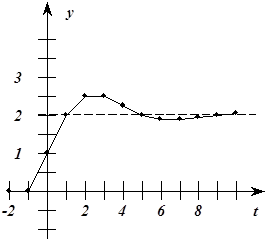
| ||||
| t | xt | yt | ||
| -2 | - | |||
| -1 | - | |||
| 1,000 | ||||
| 2,000 | ||||
| 2,500 | ||||
| 2,500 | ||||
| 2,250 | ||||
| 2,000 | ||||
| 1,875 | ||||
| 1,875 | ||||
| 1,938 | ||||
| 2,000 | ||||
| Рис. 5.14. Траектория движения системы (5.72). | 2,031 |
Как видно из уравнения (5.72), для определения траектории движения системы при 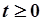 численные значения
численные значения 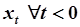 не имеют значения, требуются лишь начальные условия
не имеют значения, требуются лишь начальные условия 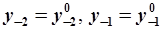 , которые в данном случае заданы нулевыми. Нулевые начальные условия
, которые в данном случае заданы нулевыми. Нулевые начальные условия 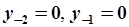 могут быть получены к моменту времени
могут быть получены к моменту времени 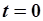 при достаточно длительном воздействии на систему сигнала
при достаточно длительном воздействии на систему сигнала 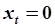 до момента
до момента 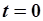 . Поэтому реакцию (рис. 5.14) можно рассматривать как реакцию на одно из типовых воздействий - ступенчатое воздействие.
. Поэтому реакцию (рис. 5.14) можно рассматривать как реакцию на одно из типовых воздействий - ступенчатое воздействие.
Идентификация параметров АРРМ.
Идентификация динамической системы заключается в отыскании математических моделей, поведение которых подобно поведению самой системы (объекта). Модель объекта необходима для синтеза законов управления, так как управление определяется в результате анализа прогноза поведения объекта [3, 14].
При использовании в качестве модели объекта АРРМ предполагается, что объект является линейным (хотя бы для рассматриваемых режимов работы) или допускает линейное описание. Строго говоря, реальные объекты являются нелинейными.
Для идентификации необходимо выбрать порядок модели (ее вид), а затем идентифицировать ее параметры (коэффициенты). Вид модели определяется аналитически, эмпирически или методом перебора из заданного “разумного” списка возможных моделей. Для каждой из них идентифицируются параметры, и оценивается ее точность. На основании анализа точности описания и сложности модели делается вывод о ее пригодности. Таким образом, выбор модели и идентификация параметров является циклическим процессом, который завершают при выборе модели, позволяющей получить удовлетворительный результат.
Идентификация параметров дискретной
модели методом наименьших квадратов.
Рассмотрим выполнение идентификации коэффициентов АРРМ методом наименьших квадратов на примерах решения задач.
Задача. Выполнить идентификацию параметров АРМ 1-го порядка.Модель имеет вид:
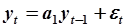 . .
| (5.82) |
Дана часть траектории, пронумеруем ее координаты, начиная с нулевого 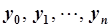 . Предположим, что эти значения измерены не точно (что компенсируется в уравнении аддитивной составляющей
. Предположим, что эти значения измерены не точно (что компенсируется в уравнении аддитивной составляющей 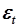 ). Эта траектория должна максимально хорошо описываться АРМ (5.82). Уравнению (5.82) можно поставить в соответствие уравнение
). Эта траектория должна максимально хорошо описываться АРМ (5.82). Уравнению (5.82) можно поставить в соответствие уравнение
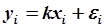 . .
| (5.83) |
Уравнение (5.83) описывает "облако" точек 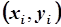 , расположенных около прямой с угловым коэффициентом
, расположенных около прямой с угловым коэффициентом 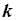 и проходящей через начало координат на плоскости (рис.5.15.).
и проходящей через начало координат на плоскости (рис.5.15.).
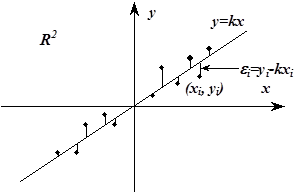 Рис. 5.15. Облако точек
Рис. 5.15. Облако точек 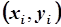 около прямой
около прямой 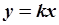 . .
| На Рис.5.15. уравнение 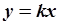 является уравнением прямой на плоскости является уравнением прямой на плоскости 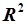 , проходящей через начало координат. В , проходящей через начало координат. В 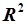 дано некоторое количество точек, расположенных в виде облака, вытянутого вдоль прямой, проходящей через начало координат. Поставим задачу определения углового коэффициента дано некоторое количество точек, расположенных в виде облака, вытянутого вдоль прямой, проходящей через начало координат. Поставим задачу определения углового коэффициента 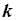 .
Решение этой математической задачи совпадает с решением исходной прикладной задачи идентификации параметра .
Решение этой математической задачи совпадает с решением исходной прикладной задачи идентификации параметра 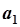 модели (5.74). модели (5.74).
|
Из рис. 5.15 видно, что некоторое (небольшое) количество точек может быть отброшено и это не повлечет существенного изменения результата. При идентификации АРРМ не все точки оказываются доступны. По данным наблюдений составляются таблицы. Данные этих таблиц являются исходными данными МНК.
Суть МНК заключается в минимизации суммы квадратов ошибок исходного уравнения (5.82) или (5.83) для данного набора точек на плоскости или координат динамической системы. Результат суммирования обозначим  , значение которого зависит от параметров системы (в данном случае
, значение которого зависит от параметров системы (в данном случае 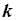 или
или 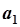 ). Далее, для наглядности, решение этих двух задач будем выполнять параллельно.
). Далее, для наглядности, решение этих двух задач будем выполнять параллельно.
Предположим, мы осуществляем наблюдение за некоторым процессом и фиксируем результаты в виде точек на плоскости. Из некоторых априорных соображений известно, что координаты точек в своей совокупности имеют линейную зависимость. Денные наблюдений занесем в таблицу 5.3.
В случае идентификации АРМ, предположим, что доступна наблюдению траектория движения системы. Координаты системы 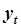 были зафиксированы и внесены в таблицу 5.4. Путем сдвига доопределим столбец
были зафиксированы и внесены в таблицу 5.4. Путем сдвига доопределим столбец 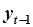 . При этом выясняется, что для момента времени
. При этом выясняется, что для момента времени 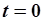 данные оказываются не определены полностью. На месте пропуска должны находиться начальные данные, которые в общем случае заранее неизвестны.\
данные оказываются не определены полностью. На месте пропуска должны находиться начальные данные, которые в общем случае заранее неизвестны.\
| Таблица 5.3 | Таблица 5.4 | |||||||||||
| i | yi | xi | t | yt | yt-1 | |||||||
| y0 | x0 | 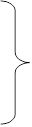
| y0 | - | 
| |||||||
| y1 | x1 | y1 | y0 | |||||||||
| y2 | x2 | y2 | y1 | |||||||||
| n+1 | … | … | … | n | ||||||||
| i | yi | xi | t | yt | yt-1 | |||||||
| … | … | … | ||||||||||
| n | yn | xn | n | yn | yn-1 | |||||||
| Y | X | Y | X |
В (5.82) и (5.83) выразим 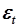 . Полученные выражения возведем в квадрат и просуммируем. Суммирование выполним по всем доступным точкам. Полученные величины обозначим
. Полученные выражения возведем в квадрат и просуммируем. Суммирование выполним по всем доступным точкам. Полученные величины обозначим 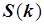 и
и  соответственно (очевидно, что результаты суммирования зависят от параметра
соответственно (очевидно, что результаты суммирования зависят от параметра 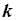 или
или 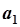 ). Модель будет наилучшим образом удовлетворять значениям таблиц, если сумма квадратов ошибок окажется минимальной:
). Модель будет наилучшим образом удовлетворять значениям таблиц, если сумма квадратов ошибок окажется минимальной:
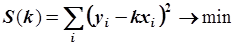 Сумма по всем точкам
Сумма по всем точкам 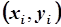
| 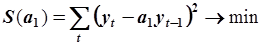 Сумма по всем доступным парам
Сумма по всем доступным парам 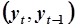 . Точка . Точка 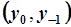 оказывается недоступной. оказывается недоступной.
|
Важно отметить, что в общем случае результат суммирования для различных наборов данных будет достигать минимума при различных значениях параметра 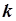 или
или 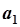 . Это означает, что точные значения этих величин определить, вообще говоря, невозможно, можно определить лишь их оценочные значения, которые в дальнейшем будем обозначать
. Это означает, что точные значения этих величин определить, вообще говоря, невозможно, можно определить лишь их оценочные значения, которые в дальнейшем будем обозначать  и
и 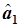 .
.
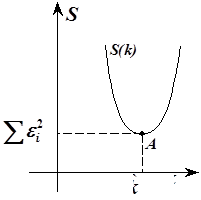 Рис.5.16. Зависимость
Рис.5.16. Зависимость  от параметра модели от параметра модели 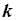 . .
|  зависит от зависит от 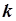 или или 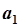 по квадратичному закону, поэтому функции по квадратичному закону, поэтому функции 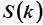 и и 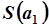 представляют собой параболы, ветви которой направлены вверх. Точка экстремума соответствует минимальному значению суммы квадратов ошибок представляют собой параболы, ветви которой направлены вверх. Точка экстремума соответствует минимальному значению суммы квадратов ошибок 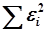 . Приравнивая производную от . Приравнивая производную от  по параметру модели к нулю можно определить его оценочное значение по параметру модели к нулю можно определить его оценочное значение  или или 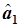 . .
|
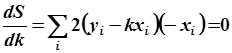
| 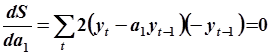
|
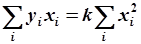
| 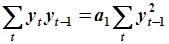
|
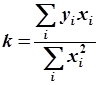 (5.83) (5.83)
| 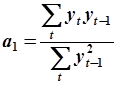 (5.83) (5.83)
|
Формулы (5.82) и (5.83) являются расчетными формулами МНК. В таблицах 5.3 и 5.4 указаны обозначения 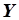 и
и 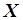 - обозначения матриц, в данном случае - векторов-столбцов. Для моделей более высокого порядка эти матрицы имеют несколько иной вид, более подробно этот вопрос будет рассмотрен ниже.
- обозначения матриц, в данном случае - векторов-столбцов. Для моделей более высокого порядка эти матрицы имеют несколько иной вид, более подробно этот вопрос будет рассмотрен ниже.
Можно показать, что более общей расчетной формулой МНК является
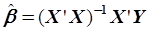 , ,
| (5.86) |
где 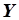 и
и 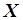 - указанные выше матрицы,
- указанные выше матрицы, 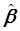 - вектор-столбец оценок параметров модели. Формула (5.86) является расчетной формулой МНК, записанная в векторно-матричной форме.
- вектор-столбец оценок параметров модели. Формула (5.86) является расчетной формулой МНК, записанная в векторно-матричной форме.
Пример. Идентификация параметров модели 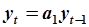
Дана траектория движения системы 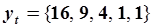 , траектория задана не точно. Выполнить идентификацию модели
, траектория задана не точно. Выполнить идентификацию модели 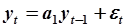 методом наименьших квадратов. Выполнить анализ случайных отклонений и прогноз координаты системы на следующий такт.
методом наименьших квадратов. Выполнить анализ случайных отклонений и прогноз координаты системы на следующий такт.
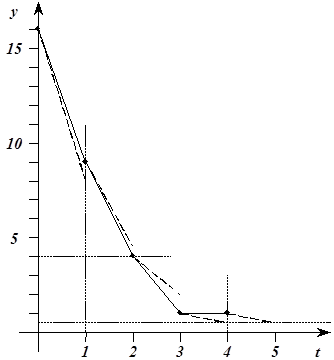 Рис. 5.17. Траектория движения системы
Рис. 5.17. Траектория движения системы 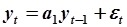
| 
| 
| 
| 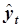
| 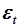
|
| - | - | ||||
| +1 | |||||
| 4.5 | -0.5 | ||||
| -1 | |||||
| 0.5 | +0.5 | ||||
| ? | 0.5 | ? | |||
МНК:
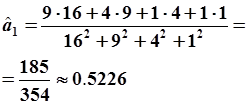 Найденное значение оценки коэффициента модели позволит определить
Найденное значение оценки коэффициента модели позволит определить 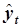 и и 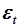 .
Если количество точек увеличить, результат может казаться иным (возможно более точным). Предположим, что в результате многочисленных экспериментов выяснилось: .
Если количество точек увеличить, результат может казаться иным (возможно более точным). Предположим, что в результате многочисленных экспериментов выяснилось:  (это позволит упросить расчеты). (это позволит упросить расчеты).
|
Выполним аналогичные расчеты по формуле (5.86). В данном случае вектор столбец 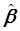 состоит из единственного коэффициента
состоит из единственного коэффициента 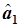 .
.
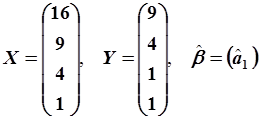 . .
| (5.87) | ||
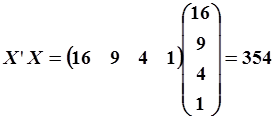 , ,
| 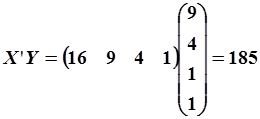
| ||
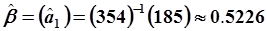 . .
| (5.89) | ||
Основным результатом задачи является значение единственного коэффициента модели 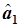 , численное значение, которого найдено при помощи расчетной формулы МНК. Модель имеет вид
, численное значение, которого найдено при помощи расчетной формулы МНК. Модель имеет вид 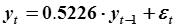 . Важно отметить, что как только оценка параметра
. Важно отметить, что как только оценка параметра 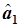 , оказывается доступной, оказывается возможным фиксация и анализ ошибок
, оказывается доступной, оказывается возможным фиксация и анализ ошибок 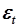 для каждого шага. Анализ этих значений в совокупности для всех доступных точек траектории позволит предсказать движение системы для тех точек, которые еще не реализованы [7, 14, 15, 19]. В данном случае координата точки
для каждого шага. Анализ этих значений в совокупности для всех доступных точек траектории позволит предсказать движение системы для тех точек, которые еще не реализованы [7, 14, 15, 19]. В данном случае координата точки 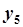 неизвестна, но после анализа последовательности
неизвестна, но после анализа последовательности 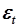 , и определения статистических характеристик, координату
, и определения статистических характеристик, координату 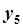 оказывается возможным предсказать с определенной степенью вероятности.
оказывается возможным предсказать с определенной степенью вероятности.
Для анализа ошибок может быть применена теория множеств. Предположим, что в результате анализа выяснилось, что 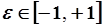 и распределена равномерно на указанном отрезке. Найдем вероятность
и распределена равномерно на указанном отрезке. Найдем вероятность 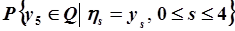 , где
, где 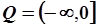 , то есть координата окажется отрицательной. Искомая вероятность равна
, то есть координата окажется отрицательной. Искомая вероятность равна  где
где
 . Из рис. 5.18 видно, что
. Из рис. 5.18 видно, что 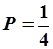

Рис. 5.18. Пересечение областей 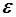 и
и 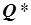 .
.
Таким образом, вероятность того, что для данной траектории при 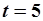 координата системы окажется отрицательной равна
координата системы окажется отрицательной равна 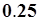 .
.
Задача. Идентификация АРРМ с двумя параметрами.
Приведем аналогии в постановках данной и предыдущей задачи:
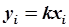 - уравнение прямой в - уравнение прямой в 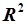 , проходящей через начало координат. , проходящей через начало координат.
| 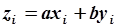 - уравнение плоскости в - уравнение плоскости в 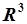 , проходящей через начало координат. , проходящей через начало координат.
|
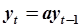 - АРМ 1-го порядка - АРМ 1-го порядка
| 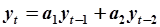 - АРМ 2-го порядка - АРМ 2-го порядка
|
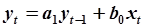 - АРРМ, простейшая модель системы “вход-выход” - АРРМ, простейшая модель системы “вход-выход”
|
В качестве отдельной задачи будет рассмотрена идентификация модели 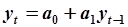 .
.
Рассмотрим следующие модели:
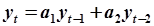
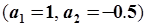
| 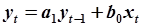
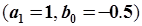
| 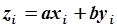
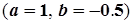
| |||||||||||||
| t | yt | yt-1 | yt-2 | t | yt | yt-1 | xt | i | zi | xi | yi | ||||
| -2 | - | - | -2 | - | - | - | - | - | - | ||||||
| -1 | - | -1 | - | - | - | - | - | ||||||||
| -4 | -4 | -4 | |||||||||||||
| -4 | -4 | -4 | -4 | -4 | -4 | ||||||||||
| -2 | -4 | -4 | -2 | -4 | -4 | -2 | -4 | -4 | |||||||
| -2 | -4 | -2 | -4 | -2 | -4 | ||||||||||
| -2 | -2 | -2 | |||||||||||||
| Y | X | Y | X | Y | X | ||||||||||
АРМ. 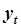 строится
по строится
по 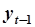 и и 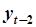
| АРРМ. 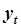 строится
по строится
по 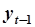 и и 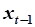
| Уравнение плоскости в пространстве. Определяя величины 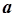 и и 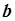 можно восстановить поверхность. можно восстановить поверхность.
|
Для наглядности вычислений внесем числовые значения. Значения в таблицах получены из АРМ при фиксированных параметрах 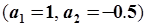 и не содержат помехи. Серым цветом в таблицах обозначены начальные данные, которые были использованы при создании таблиц. Начальные данные неизвестны на этапе наблюдения за движением системы и не могут быть использованы при идентификации.
и не содержат помехи. Серым цветом в таблицах обозначены начальные данные, которые были использованы при создании таблиц. Начальные данные неизвестны на этапе наблюдения за движением системы и не могут быть использованы при идентификации.
Сумма квадратов ошибок зависит от двух параметров 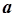 и
и 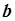 . Сумму необходимо минимизировать путем варьирования обеих параметров.
. Сумму необходимо минимизировать путем варьирования обеих параметров.
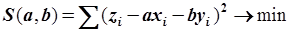
| (5.78) |
Сумма вычисляется по всем доступным точкам. Для определения минимума, частные производные по 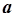 и
и 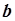 приравниваются к нулю. Из полученной системы уравнений определяются численные значения
приравниваются к нулю. Из полученной системы уравнений определяются численные значения 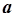 и
и 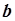 .
.
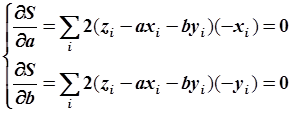
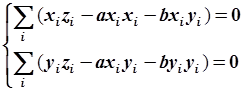
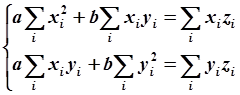 или
или
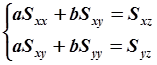
| (5.79) |
где введены следующие обозначения:
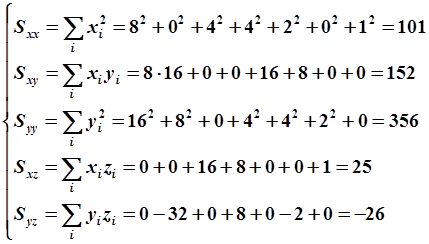
Разрешая систему относительно 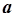 и
и 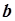 , получаем:
, получаем:
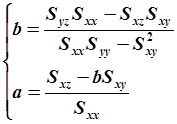
После подстановки численных значений получаем 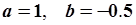 .
.
Ту же задачу можно записать и решить в матричном виде, что позволит обобщить решение на многомерный случай, что необходимо для идентификации АРРМ высокого порядка. Запишем (5.85) в следующем виде:
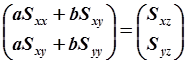 ,
,
откуда получаем
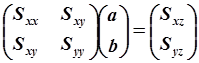 , ,
| (5.86) |
где
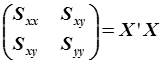 , , 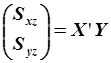 , , 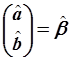 . .
| (5.87) |
Для идентификации системы необходимо найти вектор-столбец 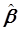 . Разрешим (5.86) относительно
. Разрешим (5.86) относительно 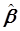 :
:
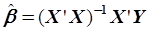 . .
| (5.88) |
Подставим в (5.87), а затем (5.86) численные значения.
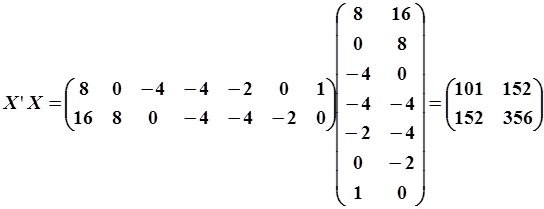
| (5.87) |
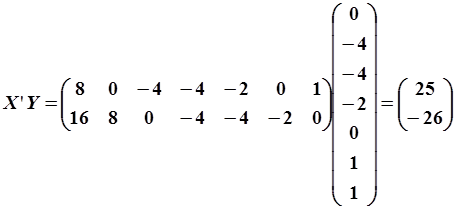 . .
| (5.88) |
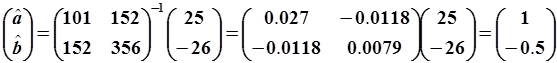 . .
| (5.89) |
Обратная матрица для произвольной матрицы 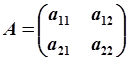 размером
размером 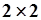 может быть найдена следующим образом:
может быть найдена следующим образом: 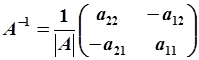 , где
, где 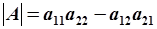 - определитель матрицы
- определитель матрицы 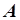 .
.
Задача. Выполнить идентификацию системы
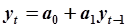 . .
| (5.90) |
по имеющейся последовательности 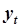 . Составим таблицу значений и по данным таблицы - матрицы
. Составим таблицу значений и по данным таблицы - матрицы 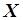 и
и 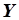 .
.
| t | yt | yt-1 | ||||||
| y0 | - | 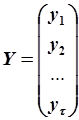
| 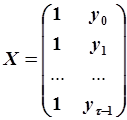
| |||||
| y1 | y0 | |||||||
| y2 | y1 | |||||||
| y3 | y2 | |||||||
| … | … | … | … | |||||
| t | yt | yt-1 | ||||||
| Y | X |
Отметим, что при коэффициенте 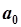 отсутствует компонент вектора
отсутствует компонент вектора 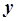 , поэтому в таблице на соответствующем месте должен стоять столбец единиц.
, поэтому в таблице на соответствующем месте должен стоять столбец единиц.
Пример. Выполнить идентификацию АРМ (5.90) по заданной последовательности 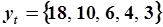 . Запишем матрицы
. Запишем матрицы 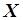 ,
, 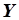 и выполним вычисления
и выполним вычисления 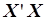 и
и 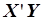 :
:
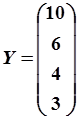
| 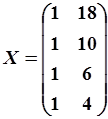
| 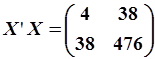
| 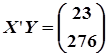
|
Подставляя полученные матрицы в (5.88) получаем:
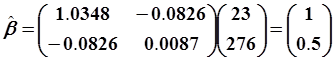 .
.
Найденные параметры модели (5.90) 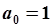 ,
, 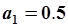 удовлетворяют исходной траектории, что легко проверяется подстановкой.
удовлетворяют исходной траектории, что легко проверяется подстановкой.
Задача. Идентификация АРРМ высокого порядка.
Как было отмечено выше, для идентификации АРРМ высокого порядка решение удобно записывать в матричном виде (5.86). Обобщим построение таблиц 5.3 и 5.4 на более общий случай для АРРМ (5.68) и для уравнения плоскости в 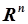 вида
вида
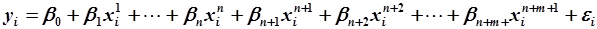 . .
| (5.91) |
получаем:
Таблица 5.5

| ||||||||||
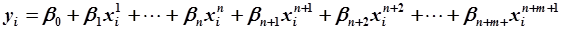
| ||||||||||
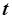
| 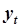
| 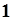
| 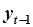
| … | 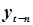
| 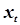
| 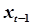
| … | 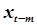
| |
| 
| 
| 
| … | 
| 
| 
| … | 
| |
| 
| 
| - | … | - | 
| - | … | - | |
| 
| 
| 
| … | - | 
| 
| … | - | |
| 
| 
| 
| … | - | 
|