Регрессионные методы позволяют выявить связи между переменными, причем особенно эффективно, если эти связи не совершенны или не имеют точного функционального описания между этими переменными. В эконометрическом анализе используются независимые переменные хi и одна зависимая переменная y. Регрессией в общем виде представляется функцией следующего вида
 (2.1)
(2.1)
где  - известные коэффициенты регрессии;
- известные коэффициенты регрессии;
xi - переменная. В эконометрическом анализе переменные представляют собой статистические данные, например стоимость товара, объем продаж, курс валюты. Так как эти данные чаще всего «привязаны» ко времени, то в эконометрических моделях используют и другие обозначения переменных, такие как Xt, где индекс t обозначает, что мы используем временной ряд.
e - невязка (ошибка, отклонение), обусловленная недостаточной пригодностью модели и ошибкой данных. Обычно эти причины являются смешанными.
Обозначения в модели 2.1 интерпретируются достаточно просто. Например, сумму
 можно представить как сумму произведений коэффициента b и переменной х
можно представить как сумму произведений коэффициента b и переменной х
 .
В последующем для упрощения выражений знак суммы мы будем обозначать без индексов, как .
В последующем для упрощения выражений знак суммы мы будем обозначать без индексов, как  . .
|
В том случае, если исследуется влияние одной переменной или фактора, то выражение (2) упрощается к виду
 (2.2)
(2.2)
Выражение (2) представляет собой линейную однофакторную регрессию. Геометрический смысл уравнения 2.2 поясним на рис. 1.
 Пусть мы имеем четыре измерения переменной х, которые имеют конкретное значение р1,р2, р3, р4. Этим значениям соответствуют определенные значения зависимой переменной y. Тогда уравнение регрессии 2.2 представляет собой прямую линию проведенную определенным образом через точки р1,р2, р3, р4. Так как истинное значение переменной нам неизвестно, то мы предполагаем, что оно располагается на этой прямой в точках Q1, Q2, Q3, Q4. Свободный член а уравнения 2.2 имеет реальный экономический смысл. Это минимальное или максимальное значение зависимой переменной (результативного признака).
Пусть мы имеем четыре измерения переменной х, которые имеют конкретное значение р1,р2, р3, р4. Этим значениям соответствуют определенные значения зависимой переменной y. Тогда уравнение регрессии 2.2 представляет собой прямую линию проведенную определенным образом через точки р1,р2, р3, р4. Так как истинное значение переменной нам неизвестно, то мы предполагаем, что оно располагается на этой прямой в точках Q1, Q2, Q3, Q4. Свободный член а уравнения 2.2 имеет реальный экономический смысл. Это минимальное или максимальное значение зависимой переменной (результативного признака).
Коэффициент b представляет собой постоянную величину, равную отношению

Природа ошибки e
Существует, по крайней мере, две причины появления в модели 2.2 этой ошибки или как ее еще называют – возмущение.
1. Наша модель является упрощением действительности и на самом деле есть еще и другие параметры, от которых зависит переменная y. Например, расходы на питания в семье зависят от размера заработной платы членов семьи, национальных и религиозных традиций, уровня инфляции и т.д.
2. Скорее всего, наши измерения содержат ошибки наблюдения. Например, данные по расходам семьи на питание составляются на основе а опроса и эти данные не всегда отражают истинное значение параметров. Необходимо отметить, что любые формы наблюдения, включая документальный содержат ошибки.
Таким образом, можно считать, что ошибка e есть случайная величина с некоторой функцией распределения.
Для нахождения коэффициентов уравнений (2.1) и (2.2) используется метод наименьших квадратов. Сущность метода заключается в том, чтобы минимизировать сумму квадратов отклонений
 , (2.3)
, (2.3)
и где  - значение результата, вычисленное по уравнению (2) в точке xi ;
- значение результата, вычисленное по уравнению (2) в точке xi ;
yi - экспериментальное значение результата в этой же точке.
Рассмотрим задачу «наилучшей» аппроксимации набора наблюдений Yt,, t = 1,..., n, линейной функцией (2.2) минимизацией функционала
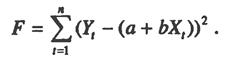
Запишем необходимые условия экстремума


Раскроем скобки и получим стандартную форму нормальных уравнений (для краткости опустим индексы суммирования у знака суммы):
 
| (2.4) |
а, b – решения системы (2.4) можно легко найти:


| (2.5) |
Порядок построения эконометрической модели рассмотрим на следующем примере [3].
В таблице 2 представлены статистические данные о расходах на питание душевом доходе для девяти групп семей. Требуется проанализировать зависимость величины расходов на питание от величины душевого дохода.
В соответствии с этим первый показатель будет результативным признаком, который обозначим у, а другой будет факторным признакам, или просто фактором, и мы обозначим его соответственно х1. Это обозначение не случайно, в последующем примере мы рассмотрим более сложную модель, в которой будет два фактора х1 и х2.
Таблица 2
| Номер группы | Расход на питание (у) | Душевой доход (х1) |
Рассмотрим однофакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х1).
Расчеты проведем в таблице 3.
Таблица 3
| Номер группы | Расход на питание (у) | Душевой доход (х1) | Y Х1 | Х12 |
| S = 11826 | S = 54725 | S = 98056440 | S = 575906797 |
Используя данные табл.3, и (2.4) получим систему уравнений:

| (2.5) |
Можно найти значения коэффициентов по формулам 2.5, но мы покажем как можно использовать более общий подход к решению задачи по правилу Крамера, для этого найдем значения определителей системы (2.5):

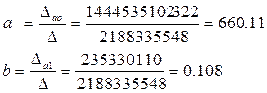
Тот же результат можно получить, используя формулы 2.5.


Таким образом, модель имеет вид:
| y = 660,11 + 0,108 Х1 | (2.6) |
Уравнение (2.6) называется уравнением регрессии, коэффициент b — коэффициентом регрессии. Направление связи между у и x1 определяет знак коэффициента регрессии а1. В нашем случае данная связь является прямой и положительной.
Вычислим дисперсии оценок а и b. Известно [1], что дисперсии оценок а и b можно определить как
|


|
 - дисперсия
- дисперсия  ;
;
 отклонения исходной выборки от среднего значения;
отклонения исходной выборки от среднего значения;
|
 , среднее значение;
, среднее значение;
 - значения расходов на питание, вычисленные по модели 2.6
- значения расходов на питание, вычисленные по модели 2.6
Для проведения расчетов дисперсий полученных оценок используем таблицу 4
Таблица 4
| №№ | Y | X | X2 | 
| 
| 
| 
| 
|
| -294 | -5453 | |||||||
| -214 | -4504 | |||||||
| -47 | -3422 | |||||||
| -2380 | ||||||||
| -1285 | ||||||||
| -155 | ||||||||
| -280 | ||||||||
| S=11826 |  6081 6081
| S=575906797 | S=367255 | S=243148394 |





