Цели анализа временных рядов. При практическом изучении временных радов на основании экономических данных на определенном промежутке времени эконометрист должен сделать выводы о свойствах этого ряда и о вероятностном механизме, порождающем этот ряд. Чаще всего при изучении временных рядов ставятся следующие цели:
1. Краткое (сжатое) описание характерных особенностей ряда.
2. Подбор статистической модели, описывающей временной ряд.
3. Предсказание будущих значений на основе прошлых наблюдений.
4. Управление процессом, порождающим временной ряд.
На практике эти и подобные цели достижимы далеко не всегда и далеко не в полной мере. Часто этому препятствует недостаточный объем наблюдений из-за ограниченного времени наблюдений. Еще чаще – изменяющаяся с течением времени статистическая структура временного ряда.
Стадии анализа временных рядов. Обычно при практическом анализе временных рядов последовательно проходят следующие этапы:
1. Графическое представление и описание поведения временного рада.
2. Выделение и удаление закономерных составляющих временного рада, зависящих от времени: тренда, сезонных и циклических составляющих.
3. Выделение и удаление низко- или высокочастотных составляющих процесса (фильтрация).
4. Исследование случайной составляющей временного ряда, оставшейся после удаления перечисленных выше составляющих.
5. Построение (подбор) математической модели для описания случайной составляющей и проверка ее адекватности.
6. Прогнозирование будущего развития процесса, представленного временным рядом.
7. Исследование взаимодействий между различными временными радами.
Для решения этих задач существует большое количество различных методов. Из них наиболее распространенными являются следующие:
8Корреляционный анализ, позволяющий выявить существенные периодические зависимости и их лаги (задержки) внутри одного процесса (автокорреляция) или между несколькими процессами (кросскорреляция).
9Спектральный анализ, позволяющий находить периодические и квазипериодические составляющие временного ряда.
10Сглаживание и фильтрация, предназначенные для преобразования временных рядов с целью удаления из них высокочастотных или сезонных колебаний.
11Модели авторегрессии и скользящего среднего, которые оказываются особенно полезными для описания и прогнозирования процессов, проявляющих однородные колебания вокруг среднего значения.
12Прогнозирование, позволяющее на основе подобранной модели поведения временного рада предсказывать его значения в будущем.
Тема 12. Модели тренда
ростейшие модели тренда. Приведем модели трендов, наиболее часто используемые при анализе экономических временных рядов, а также во многих других областях. Во-первых, это простая линейная модель
 (3.1)
(3.1)
где а0, а1 – коэффициенты модели тренда;
t – время.
В качестве единицы времени может быть час, день (сутки), неделя, месяц, квартал или год. Модель 3.1. несмотря на свою простоту, оказывается полезной во многих реальных задачах. Если нелинейный характер тренда очевиден, то может подойти одна из следующих моделей:
1. Полиномиальная:

 (3.2)
(3.2)
где значение степени полинома п в практических задачах редко превышает 5;
2. Логарифмическая:
 (3.3)
(3.3)
Эта модель чаще всего применяется для данных, имеющих тенденцию сохранять постоянные темпы прироста;
3. Логистическая:
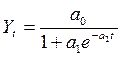 (3.4)
(3.4)
Гомперца
 (3.5), где
(3.5), где 
Две последние модели задают кривые тренда S-образной формы. Они соответствуют процессам с постепенно возрастающими темпами роста в начальной стадии и постепенно затухающимитемпами роста в конце. Необходимость подобных моделей обусловлена невозможностью многих экономических процессов продолжительное время развиваться с постоянными темпами роста или по полиномиальным моделям, в связи с их довольно быстрым ростом (или уменьшением).
При прогнозировании тренд используют в первую очередь для долговременных прогнозов. Точность краткосрочных прогнозов, основанных только на подобранной кривой тренда, как правило, недостаточна.
Для оценки и удаления трендов из временных рядов чаще всего используется метод наименьших квадратов. Этот метод достаточно подробно рассматривался во втором разделе пособия в задачах линейного регрессионного анализа. Значения временного ряда рассматриваюткак отклик (зависимую переменную), а время t – какфактор, влияющий на отклик (независимую переменную).
Для временных рядов характерна взаимная зависимость его членов (по крайней мере, не далеко отстоящих по времени) и это является существенным отличием от обычного регрессионного анализа, для которого все наблюдения предполагаются независимыми. Тем не менее, оценки тренда и в этих условиях обычно оказываются разумными, если выбрана адекватная модель тренда и если среди наблюдений нет больших выбросов. Упомянутые выше нарушения ограничений регрессионного анализа сказываются не столько на значениях оценок, сколько наих статистических свойствах. Так, при наличии заметной зависимости между членами временного ряда оценки дисперсии, основанные на остаточнойсумме квадратов (2.3), дают неправильные результаты. Неправильными оказываются и доверительные интервалы для коэффициентов модели, и т.д. В лучшем случае их можно рассматривать как очень приближенные.
Это положение может быть частично исправлено, если применять модифицированные алгоритмы метода наименьших квадратов, такие как взвешенный метод наименьших квадратов. Однако для этих методов требуется дополнительная информация о том, как меняется дисперсия наблюдений или их корреляция. Если же такая информация недоступна, исследователям приходится применять классический метод наименьших квадратов, несмотря на указанные недостатки.