Какова природа ошибки e?

Существует, по крайней мере, две причины появления в модели 2.2 этой ошибки:

1. Наша модель является упрощением действительности и на самом деле есть еще и другие параметры, от которых зависит переменная y. Например, расходы на питания в семье зависят от размера заработной платы членов семьи, национальных и религиозных традиций, уровня инфляции и т.д.

2. Скорее всего, наши измерения содержат ошибки. Например, данные по расходам семьи на питание составляются на основе анкетного опроса и эти данные не всегда отражают истинное значение параметров.

Таким образом, можно считать, что ошибка e есть случайная величина с некоторой функцией распределения.

Для нахождения коэффициентов уравнений (2.1) и (2.2) используется метод наименьших квадратов. Сущность метода заключается в том, чтобы минимизировать сумму квадратов отклонений

, (2.3)

где 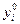- значение результата, вычисленное по уравнению (2) в точке x_i;

y_i - экспериментальное значение результата в этой же точке.

Рассмотрим задачу «наилучшей» аппроксимации набора наблюдений Y_t,, t = 1,..., n, линейной функцией (2.2) минимизацией функционала

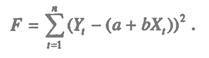
Запишем необходимые условия экстремума

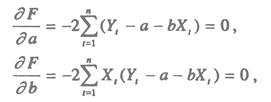
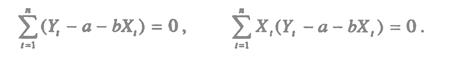
Раскроем скобки и получим стандартную форму нормальных уравнений (для краткости опустим индексы суммирования у знака суммы):

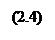
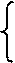
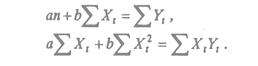
а, b – решения системы (2.4) можно легко найти:

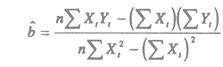
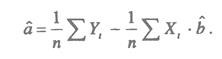
Порядок построения эконометрической модели рассмотрим на следующем примере [3].

В таблице 2 представлены статистические данные о расходах на питание и душевом доходе для девяти групп семей. Требуется проанализировать зависимость величины расходов на питание от величины душевого дохода.

В соответствии с этим первый показатель будет результативным признаком, который обозначим у, а другой будет факторным признакам, или просто фактором, и мы обозначим его соответственно х₁. Это обозначение не случайно, в последующем примере мы рассмотрим более сложную модель, в которой будет два фактора х₁ и х₂.

Таблица 2


Номер группы	Расход на питание (у)	Душевой доход (х₁)

Рассмотрим однофакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х₁).

Расчеты проведем в таблице 3.

Таблица 3


Номер группы	Расход на питание (у)	Душевой доход (х₁)	Y Х₁	Х₁²









	S = 11826	S = 54725	S = 98056440	S = 575906797

Используя данные табл.3, и (2.4) получим систему уравнений:

(2.5)

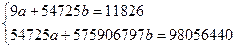
Можно найти значения коэффициентов по формулам 2.5, но мы покажем как можно использовать более общий подход к решению задачи по правилу Крамера, для этого найдем значения определителей системы (2.5):

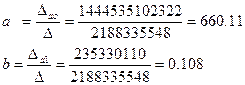
Тот же результат можно получить, используя формулы 2.5.

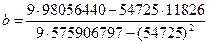
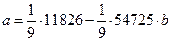
Таким образом, модель имеет вид:

(2.6)

y = 660,11 + 0,108 Х₁

Уравнение (2.6) называется уравнением регрессии, коэффициент b — коэффициентом регрессии. Направление связи между у и x₁ определяет знак коэффициента регрессии а₁. В нашем случае данная связь является прямой и положительной.

Вычислим дисперсии оценок а и b. Известно [1], что дисперсии оценок а и b можно определить как

(2.7)

(2.8)

где

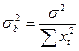
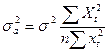
- дисперсия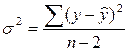

;

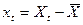отклонения исходной выборки от среднего значения;

(2.9)

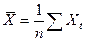, среднее значение;

- значения расходов на питание, вычисленные по модели 2.6

Для проведения расчетов дисперсий полученных оценок используем таблицу 4

Таблица 4


№№	Y	X	X²
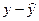
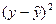
				-294		-5453
				-214		-4504
				-47		-3422
						-2380
						-1285
						-155


				-280
	S=11826	6081	S=575906797		S=367255		S=243148394

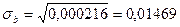
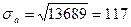
Следующий этап – оценка значимости коэффициентов полученной модели. На этом этапе проверяется статистическая гипотеза о равенстве нулю коэффициентов модели а и b. Проверяем гипотезу Н₀: b=0 против гипотезы Н₁:b#0 при заданном уровне значимости гипотезы a. Обычно a =0.05. При проверке используется распределение Стьюдента. Для этого рассчитывают значение t-критерия для исходной выборки наблюдений по формуле

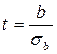(2.10)

Затем сравнивают его с табличным значением с (n-2) степенями свободы при заданной степени свободы. Это значение берут из таблицы значений t -критерия (приложение 4, таблица 2). Для a =0,05 при степени своды равном 7 табличное значение t –критерия (t_p) равно 2,37. Если расчетное значение критерия больше табличного, то гипотеза Н₀ отклоняется и принимается гипотеза Н₁: значение коэффициента отличается от 0. В нашем случае 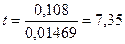. Так как 7,35>2,37, то делаем вывод о значимости коэффициента b в модели. Расчетное значение t-критерия для коэффициента а равно 5,62, что тоже свидетельствует о его значимости в модели.

Для оценки тесноты связи модели с исходными данными рассчитывается коэффициент детерминации

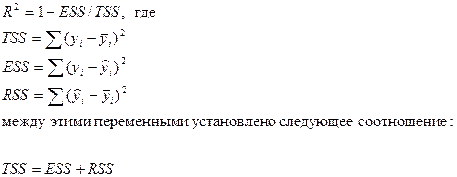(2.11)

Для определения коэффициента детерминации проведем расчеты с использованием таблицы 5.

Таблица 5

№№ Y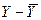

-53

-127

-188

-200

-244

S=11826 S=367383

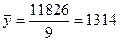
Значения ESS возьмем из таблицы 4.

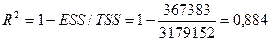
Коэффициент детерминации показывает долю изменения (вариации) результативного признака под действием факторного признака. В нашем случае R ² = 0,884, а это означает, что фактором душевого дохода можно объяснить почти 88% изменения расходов на питание.

Коэффициент корреляции можно определить как

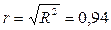(2.12)

Чем ближе значение коэффициента корреляции к единице, тем теснее корреля-ционная связь. Полученное значение коэффициента корреляции свидетельствует, что связь между расходами на питание и душевым доходом очень тесная.

Коэффициенты регрессии (в рассматриваемом случае это коэффициент b) нельзя использовать для непосредственной оценки влияния факторов на результативный признак из-за различия единиц измерения исследуемых показателей. Для этих целей вычисляются коэффициенты эластичности.

Коэффициент эластичности для рассматриваемой модели парной регрессии рассчитывается по формуле:

(2.13)

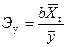
Он показывает, насколько процентов изменяется результативный признак у при изменении факторного признака X_t на один процент.

В нашем примере коэффициент эластичности расходов на питание в зависимости от душевого дохода будет равен

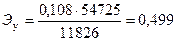
Это означает, что при увеличении душевого дохода на 1 % расходы на питание увеличатся на 0,49 %.

Качество эконометрических моделей может быть установлено на основе анализа остаточной последовательности. Остаточная последовательность проверяется на выполнение свойств случайной компоненты экономического ряда: близость нулю выборочного среднего, случайный характер отклонений, отсутствие автокорреляции и нормальность закона распределения.

О качестве моделей регрессии можно судить также по значениям коэффициента корреляции и коэффициента детерминации для однофакторной модели. Чем ближе абсолютные величины указанных коэффициентов к 1, тем теснее связь между изучаемым признаком и выбранными факторами и, следовательно, с тем большей уверенностью можно судить об адекватности построенной модели, включающей в себя наиболее влияющие факторы.

Для оценки точности регрессионных моделей обычно используются, средняя относительная ошибка аппроксимации (2.11).

Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как

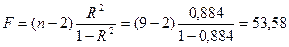(2.14)

Расчетное значение F-критерия сравнивают c табличным (таблица 1, приложения 4) при заданном уровне значимости гипотезы (обычно 0,05) и степенях свободы f₁= n – 1 и f₂= n - m - 1, где n – обьем выборки, m – число включенных факторов в модель.

Для нашего случая f₁ = 8, f₂ = 7. Табличное значение F – критерия находим по таблице 2 приложения 4 F_t = 3,50.

Если расчетное значение F – критерия больше табличного, то модель считается адекватной исходным данным.

В нашем случае 53,50 > 3,50, следовательно, модель значима и адекватно описывает исходные данные.

Эти же расчеты можно выполнить значительно быстрее при использовании ЭВМ. В электронных таблицах EXCEL в разделе меню СЕРВИС при полной инсталляции пакета присутствует функция АНАЛИЗ. При выборе этой функции открывается окно (рис.2). В предлагаемом перечне необходимо выбрать раздел регрессия и в появившейся форме необходимо заполнить соответствующие поля. Исходные данные необходимо представить на рабочем листе в виде, показанном на рис.3.

На рис. 4 представлена форма с заполненными исходными данными для проведения регрессионного анализа.

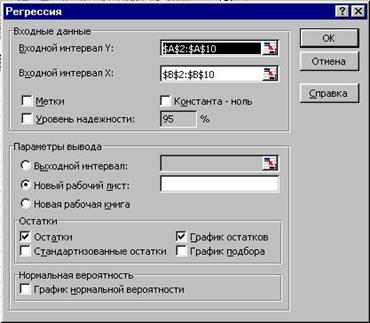
Рис. 4

После нажатия клавиши OK, проводится расчет и результаты заносятся на новый лист в следующем виде (рис. 5).

ВЫВОД ИТОГОВ

Регрессионная статистика

Множественный R 0,94046717

R-квадрат 0,8844785

Нормированный R-квадрат 0,86797542

Стандартная ошибка 229,054087

Наблюдения

df SS MS F Значимость F

Регрессия 53,594779 0,000159874

Остаток 367260,4 52465,77

Итого

Коэффициенты Стандартная ошибка t-статистика P-Значение Нижние 95%

Y-пересечение 660,106766 117,5052 5,61768 0,000801 382,2512536

Переменная X 1 0,1075384 0,014689 7,320845 0,0001599 0,072803654

Рис. 5. Результаты расчетов в электронных таблицах EXCEL

Использование электронных таблиц EXCEL позволяет обойтись без таблиц с критическими значениями t-критерия и F-критерия. В результатах расчетов появляются новые значения Значимость F и Значимость t, которое определяет расчетный уровень значимости F и t-критериев по заданным исходным данным. Если это значение меньше заданного (0,05), то модель считается адекватной исходным данным и значимой.

Какова природа ошибки e?

Поиск по сайту