В этом параграфе изучается одна из важнейших теорем геометрии - теорема Пифагора и обратная ей теорема. Теорема Пифагора позволят значительно расширить круг задач, решаемых в курсе геометрии. На ней в значительной мере базируется дальнейшее изложение теоретического курса.
В результате изучения данного параграфа учащиеся должны:
знать формулировки теоремы Пифагора и следствий из неё; уметь воспроизводить доказательство теоремы Пифагора, применять ее при решении задач.
Чтобы теорема заинтересовала учеников и была ими усвоена, нужна основательная, всесторонняя подготовка. Не заинтересовавшиеся не будут слушать (слушать «пассивно»), и урок потеряет смысл, не будет уроком.
Перед доказательством теоремы Пифагора желательно провести подготовительную работу по готовым чертежам и повторить основные понятия, определения, термины; свойства площадей, так как в доказательстве используется площадь прямоугольника.
При проведении доказательства теоремы Пифагора полезно подвести учеников к тому, чтобы они приняли пассивное участие в составлении формулировки теоремы; освоили формулировку, выделили условие и заключение. Учитель должен, заранее заготовив чертёж, необходимый для доказательства теоремы, наглядно показывать на чертеже этапы проведения доказательства.
Необходимо, чтобы ученики имели опыт в решении задач; освоили первые шаги (умели сделать чертёж как можно близкий к усвоению, внести в него всё, что дано в условии, ввести необходимые обозначения), записать условие и заключение, используя введённые обозначения; Владели элементарными навыками поиска решения задач.
Для закрепления теоремы можно предложить учащимся следующие устные задачи на вычисление:
а) Катеты прямоугольного треугольника 6 см и 8 см. Вычислите гипотенузу треугольника.
б) Гипотенуза прямоугольного треугольника равна 5 см, а один из катетов 3 см. Определите второй катет.
Вопросами для повторения предусматриваются доказательства следствий из теоремы Пифагора. Эти доказательства просты и в явном виде в учебном пособии отсутствуют. При разборе этих доказательств в классе можно предложить учащимся записать их в тетради.
Ещё одним подходом к изучению теоремы Пифагора, является метод проблемной ситуации на уроках геометрии.
Учебный процесс совершается более активно в тех случаях, когда он связан с решением задач пробных ситуаций, а проблемы имеют мотивационную основу, включая живой интерес к предмету изучения. Мотивы стимулируют, организуют и направляют учебную деятельность. Значительный интерес представляет мотивация для организации процесса обучения и направления мыслительной деятельности учеников.
Проблемы, которые учитель может ставить перед учениками, обычно разрешаются на протяжении одного или нескольких уроков.
Наиболее часто учителя создают проблемные ситуации при помощи эксперимента, то есть исследования частного случая.
Легко организовать проблемную ситуацию, предложив ученикам задачи, для решения которых нужны новые знания. Полезно при этом поддерживать накал активности цепью проблемных вопросов, сменяющих один другой.
Перед изучением теоремы Пифагора рассматривается практическая задача, для решения которой нужно уметь вычислить длину гипотенузы по длинам катетов.
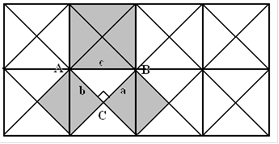
Построение убеждает, что определенная зависимость между катетами и гипотенузой существует, что два катета определяют треугольник, в котором гипотенуза не может быть произвольной. Можно найти приблизительное решение графическим путем. Теперь возникает вопрос: «Можно ли выразить формулой зависимость между катетами и гипотенузой?». В поисках ответа рассмотрим удобный частный случай: прямоугольный треугольник с острыми углами по 45º.
Получаем для него формулу
c2 = a2 + b2 и задаёмся вопросом: «Верна ли эта формула для произвольного прямоугольного треугольника?».
Дальнейшее исследование может быть построено по такой схеме. Поскольку в предлагаемую формулу входят величины a2, b2, c2, то есть площади квадратов со сторонами a, b, c. Построим эти квадраты. Первое построение («пифагоровы штаны») идею доказательства не поясняет.
Тогда учитель предлагает связать величины a, b и c в комбинации прямоугольных треугольников и квадратов таким образом, каким показано на рисунке.
Рассмотрим данный рисунок. Понятно, что с одной стороны площадь большого квадрата равна произведению двух сторон, которые выражены как (a+b). Отсюда следует, что площадь равна (a+b)2.
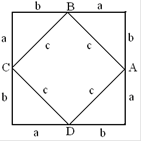
С другой стороны площадь большого квадрата равна сумме площадей фигур, на которые разбит данный квадрат. В данном случае, это сумма малого квадрата со стороной c и четырёх равных треугольников со сторонами a, b и c.
Отсюда следует, что площадь малого квадрата равна разности площади большого квадрата со стороной (a+b) и учетверённой площади треугольника со сторонами a, b и c, то есть
c2 = (a + b)2 -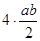 
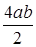2 = a2 + 2ab + b2 - 
2c2 = 2a2 + 4ab + 2b2 - 4ab
2c2 = 2a2 + 2b2
c2 = a2 + b2
Можно ли считать формулу доказанной? Если исходить из такой формулы, которая дана на чертеже, то да. Рассмотрим, всегда ли можно для любого прямоугольного треугольника провести такое построение. Строим квадрат со стороной (a + b) и строим прямоугольный треугольник с катетами a и b. Выясним, почему все такие треугольники равны. Остаётся показать, что фигура, образованная гипотенузой и полученных прямоугольных треугольников, является квадратом. Замечаем, что все стороны этой фигуры равны как гипотенузы равных треугольников. Но достаточно ли этого, чтобы фигура ABCD была квадратом? - Нет. Доказываем, что все углы этой фигуры прямые, так как они равны разности развёрнутого угла и острых углов данного прямоугольного треугольника. Следовательно, теорему Пифагора можно считать доказанной.
В качестве домашнего задания учитель может поручить ознакомиться с доказательством, данным в учебнике.
Но цепь вопросов, связанных с зависимостью сторон прямоугольного треугольника, может быть продолжена.
Спросим прежде всего: «Справедлива ли теорема Пифагора для непрямоугольных треугольников?» - Очевидно, нет, так как две стороны треугольника a и b не определяют однозначно его форму, а третья сторона меняет свою длину в зависимости от значения угла между сторонами a и b так, что a - b < c< a + b (при b < a).
Следующая проблема: «Верна ли обратная теорема, обратная теореме Пифагора?»
Если квадрат большей стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный, а именно: прямым является угол, лежащий против этой большой стороны. В самом деле, если бы это было не так и треугольник, стороны которого a, b и c связаны зависимостью
c2 = a2 + b2, оказался бы не прямоугольным, то и стороны бы его не смогли бы удовлетворять этому равенству.
Весьма полезно попросить учащихся указать ряд случаев применения теоремы Пифагора.
В поиске ответа на этот вопрос могут появиться такие задачи.
Участок земли имеет форму прямоугольного треугольника. Наибольшая сторона участка выходит к реке и заболочено, пройти по ней нельзя. Как найти длину наибольшей стороны, если другие две стороны можно измерить непосредственно?
Длина часовой стрелки часов равна 6 мм, а минутной - 8 мм, сколько времени показывают часы, если расстояние между концами стрелок равно 20 мм, а минутная стрелка стоит на отметке «12»?
Можно провести экскурс учащихся в историю, но небольшой, что бы учащимся не надоело слушать.
Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах эта теорема встречается за 1200 лет до Пифагора. Возможно, что тогда ещё не знали её доказательства, а само соотношение между гипотенузой и катетом было установлено опытным путём на основе измерений. Пифагор, по-видимому нашёл доказательство этого соотношения. Сохранилось древние предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам - даже 100 быков. На протяжении последних веков были найдены различные другие доказательства этой теоремы. В настоящее время их насчитывается боле ста.