1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями координат.
3. Найти асимптоты.
4. Найти точки возможного экстремума.
5. Найти критические точки.
6. Исследовать знак первой производной и определить участки возрастания и убывания функции, точки экстремума.
7. Исследовать знак второй производной и найти направление выпуклости графика функции и точки перегиба.
8. Учитывая исследование, построить график.
Пример. Построить график функции 
1) область определения: 
2) функция непрерывна при
- точка разрыва
3) - вертикальная асимптота
4) функция общего вида
5) не периодическая
6) пересечение с OX:
пересечение с OY:
7) при 
график функции ниже оси OX; (y< 0)
при 
график функции выше оси OX. (y> 0)
8) 
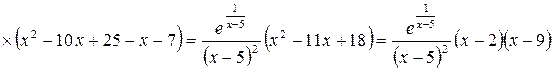
9) 
|
В точке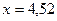 
– перегиб
10) Найдем наклонные асимптоты: 
4. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Неопределенный интеграл
Основная задача дифференциального исчисления – отыскание производной заданной функции. Интегральное исчисление решает обратную задачу: по данной функции 
найти такую 
, производная от которой равна , т.е. 
Определение 4.1. Функция называется первообразной для функции на некотором промежутке X, если для всех значений x из этого промежутка выполняется равенство
Примеры
1. Функция 
является первообразной для функции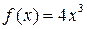 
на всей числовой прямой, так как при любом значении x 
2. Функция 
является первообразной для функции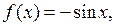 
так как при любом значении x 
3. Функция 
(где c – произвольная постоянная) является первообразной для функции 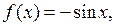так как при любом значении x 
Таким образом, задача отыскания по данной функции её первообразной решается неоднозначно.
Покажем, что множество функций 
- некоторая первообразная для функции , а c – произвольная постоянная, исчерпывает все первообразные для функции .
Ранее было доказано, что функция, производная которой на некотором промежутке X равна нулю, постоянна на этом промежутке.
Теорема 4.1. Если - первообразная для функции на некотором промежутке X, то любая другая первообразная для на том же промежутке может быть представлена в виде 
- произвольная постоянная.
Доказательство. Пусть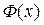 
- любая другая первообразная для функции , на промежутке X, т.е.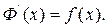 
Тогда для любого 
выполняется:
а по лемме это означает, что функция 
постоянна, т.е. 
где c – некоторое число. Получаем 
.
Из теоремы следует, что достаточно найти какую – либо одну первообразную и тогда можно назвать все семейство первообразных 
Определение 4.2. Если функция - первообразная для функции на промежутке X, то множество функций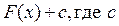 
- произвольная постоянная, называется неопределенным интегралом от функции на этом промежутке и обозначается символом
- подынтегральная функция;
- подынтегральное выражение;
x – переменная интегрирования.
Восстановление функции по её производной называется интегрированием этой функции. Интегрирование представляет собой операцию, обратную дифференцированию. Для того, чтобы проверить правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию: 
Будем говорить, что функция интегрируема, если для неё существует неопределенный интеграл.