Обобщим представление (11.1.10) на случай многократного выделения квазистатической составляющей и будем искать решение в виде [24]
| (11.2.1) |
Здесь 
– функции, определяемые ниже из соответствующих статических задач, 
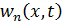- динамическая составляющая n -го порядка.
При этом предполагается, что функция 
, характеризующая изменение нагрузки во времени, является 2 n раз дифференцируемой.
Подставляя представление для перемещений (11.2.1) в уравнение (11.1.1), будем иметь
| (11.2.2) |
Сделав замену индекса j, по которому ведется суммирование в правой части равенства (11.2.2) на j=k- 1 и выделив некоторые слагаемые из сумм, равенство (11.2.2) можно представить в следующем виде
 
| (11.2.3) |
Выберем функции 
таким образом, чтобы выражения, стоящие множителями при 
(j =0, 1, …, n- 1), обратились в нули. Тогда функции будут удовлетворять следующим последовательно решаемым статическим задачам
 .
| (11.2.4) |
При условиях (11.2.4) функция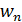 
будет удовлетворять динамическому уравнению
| (11.2.5) |
Потребуем, чтобы функции и 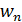удовлетворяли граничным условиям исходной задачи, тогда функция 
(11.2.1) также будет удовлетворять указанным граничным условиям.
Чтобы проследить сходимость вынуждаемой части решения, будем рассматривать далее случай нулевых начальных условий
| (11.2.6) |
Очевидно, что если будут выполняться следующие равенства для производных
| (11.2.7) |
Функция 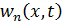, характеризующая динамическую составляющую, будет удовлетворять нулевым начальным условиям
 .
| (11.2.8) |
Условия (11.2.7) указывают на то, что функция q (t) должна быть представима в окрестности нуля следующим рядом Тейлора
| (11.2.9) |
или иметь следующую структуру
 ,
|
где q* (t) – произвольная ограниченная в нуле функция (2 n раз дифференцируемая).
Отыскивая решение уравнения (11.2.5) в виде разложения по собственным формам колебаний рассматриваемой упругой системы
| (11.2.10) |
получим следующие выражения для обобщенных координат Si
| (11.2.11) |
Предполагается, что формы ji (х) пронормированы по единичной массе.
Решение уравнения (11.2.11) при нулевых начальных данных (11.2.8) имеет вид
| (11.2.12) |
где
| (11.2.13) |
Определим коэффициенты Фурье разложения 
n - ой квазистатики, входящие в (11.2.12).
Применение к рекуррентной последовательности уравнений (11.2.4) метода разложения по собственным формам колебаний приводит к следующему значению для w 0 n
| (11.2.14) |
где Ai= { p,ji } – обобщенная сила.
Действительно, будем отыскивать решение первого уравнения (11.2.4) в виде
| (11.2.15) |
Подставив (11.2.15) в первое уравнение и учитывая следующее равенство для собственных форм колебания
 ,
| (11.2.16) |
будем иметь
| (11.2.17) |
Умножая скалярно левую и правую часть (11.2.17) на 
и учитывая ортогональность форм собственных колебаний, получим
| (11.2.18) |
Рассмотрим второе уравнение (11.2.4) (k =2) с учетом (11.2.18)
| (11.2.19) |
Аналогично (11.2.15) будем отыскивать решение (11.2.19) в виде
| (11.2.20) |
После подстановки 
из (11.2.20) в уравнение (11.2.19) и учета (11.2.16), будем иметь
| (11.2.21) |
Скалярное умножение обеих частей (11.2.21) на приводит к равенствам
| (11.2.22) |
Повторяя последовательное решение рекуррентной системы уравнений (11.2.4), получим для 
соотношение (11.2.14).
Из (11.2.14) будем иметь следующее выражение для коэффициентов Фурье
| (11.2.23) |
Подставляя Si (t) (11.2.12) с учетом (11.2.23) в равенство (11.2.10), для полей кинематических параметров 
(11.2.1) приходим к следующему окончательному выражению
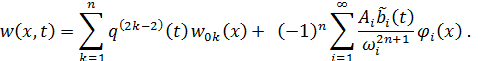
| (11.2.24) |
Без выделения квазистатической составляющей решение для имеет вид (11.1.9).
Нетрудно видеть, что сходимость ряда (11.2.24) существенно улучшена по сравнению с (11.1.9) за счет дополнительных множителей 
, причем каждое дополнительное выделение квазистатики (увеличение на единицу) приводит к ускорению сходимости на 
. В частном случае при n =1 из (11.2.24) получаем решение для случая однократного выделения квазистатической составляющей (11.1.25).
Отметим, что столь сильное влияние выделения квазистатической составляющей на сходимость решения связано с тем, что фундаментальные решения динамических задач обладают одинаковыми особенностями или главными частями со статическими в пространстве координат [6, 30]. Поэтому выделение из динамической задачи соответствующего квазистатического решения устраняет особенности и разрывы комбинаций производных, через которые выражаются кинематические и силовые факторы, и делает остающуюся часть динамического решения более гладкой и быстросходящейся. Особенно явно этот эффект прослеживается при наличии скачков во внешних нагрузках и при действии сосредоточенных сил.
Отметим также, что факт совпадения особенностей статических и динамических задач использовался при сведении граничных задач стационарных колебаний к интегральным уравнениям [17, 18] (путем выделения особенностей статической задачи и построения комбинаций специальных функций, удовлетворяющих динамической задаче, с теми же особенностями).