В предыдущем параграфе при многократном выделении квазистатической составляющей были наложены достаточно жесткие ограничения на степень гладкости функции  , характеризующей изменение нагрузки во времени и ее поведения в окрестности нуля.
, характеризующей изменение нагрузки во времени и ее поведения в окрестности нуля.
Здесь рассмотрен общий случай, когда первые 2 n производные функции  имеют разрывы первого рода (конечные скачки) в некоторой точке
имеют разрывы первого рода (конечные скачки) в некоторой точке  .
.
Пусть внешняя нагрузка, как и в разделе 1, представима в виде

| (11.3.1) |
Обозначим скачки 2 n первых производных функции в точке  через
через  k= 1,2,…,2 n
k= 1,2,…,2 n

| (11.3.2) |
Знаками "-" и "+" здесь помечены значения производных слева и справа от точки  .
.
Важным этапом для последующего решения задачи является представление производных функций  в виде суммы непрерывных и разрывных составляющих, выражающихся через функцию Хевисайда и дельта-функцию
в виде суммы непрерывных и разрывных составляющих, выражающихся через функцию Хевисайда и дельта-функцию  , умноженные на величины скачков производных (11.3.2)
, умноженные на величины скачков производных (11.3.2)
Тогда первая производная запишется так
 , ,
| (11.3.3) |
где  – непрерывная составляющая первой производной.
– непрерывная составляющая первой производной.
Вторую производную  с учетом (11.3.3) и правила дифференцирования функции Хевисайда представим в следующем виде
с учетом (11.3.3) и правила дифференцирования функции Хевисайда представим в следующем виде
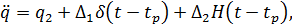
| (11.3.4) |
где  является непрерывной составляющей второй производной.
является непрерывной составляющей второй производной.
В целом, если 2 n производные функции  имеют разрывы первого рода в точке
имеют разрывы первого рода в точке  , равные
, равные  (k =1, 2, …, 2 n), то их непрерывные составляющие определяются по следующей схеме (в точке
(k =1, 2, …, 2 n), то их непрерывные составляющие определяются по следующей схеме (в точке 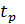 функции
функции 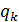 доопределяются равными своим пределам слева и справа)
доопределяются равными своим пределам слева и справа)
 , ,
 ………………………..
………………………..

| (11.3.5) |
Переходим к выделению квазистатической составляющей. При разрывных производных внешнего воздействия, в отличие от предыдущего параграфа, удобнее проводить анализ решения путем последовательного выделения квазистатики.
Итак, будем отыскивать решение задачи в виде (11.1.10) раздела 1. Тогда с учетом (11.3.4) для нахождения динамической составляющей  первого порядка приходим к следующему уравнению
первого порядка приходим к следующему уравнению

| (11.3.6) |
Представим функцию  в виде суперпозиции двух слагаемых
в виде суперпозиции двух слагаемых
 . .
| (11.3.7) |
Здесь  реакция системы на непрерывную составляющую внешнего воздействия, которая определяется из уравнения
реакция системы на непрерывную составляющую внешнего воздействия, которая определяется из уравнения

| (11.3.8) |
Функция  характеризует реакцию системы на импульсное и ступенчатое воздействие, определяемое дельта-функцией и функцией Хевисайда,
характеризует реакцию системы на импульсное и ступенчатое воздействие, определяемое дельта-функцией и функцией Хевисайда,

| (11.3.9) |
Полученная задача является типовой и будет рассмотрена ниже.
Остановимся теперь на уравнении (11.3.8). Решение уравнения (11.3.8) снова будем отыскивать, выделяя квазистатическую составляющую. При этом функцию 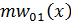 в правой части уравнения (11.3.8) можно трактовать как функцию
в правой части уравнения (11.3.8) можно трактовать как функцию  , характеризующую распределение внешней силы по координате, а функцию
, характеризующую распределение внешней силы по координате, а функцию 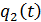 как функцию
как функцию  , характеризующую изменение внешней силы во времени.
, характеризующую изменение внешней силы во времени.
Тогда по аналогии с (11.1.10) раздела 1 решение уравнения (11.3.8) можно искать в виде

| (11.3.10) |
Подставляя представление для  из (11.3.10) в уравнение (11.3.8), будем иметь
из (11.3.10) в уравнение (11.3.8), будем иметь

| (11.3.11) |
Определим функцию  таким образом, чтобы выражение, стоящее в скобках в правой части (11.3.11), обращалось в нуль
таким образом, чтобы выражение, стоящее в скобках в правой части (11.3.11), обращалось в нуль
 . .
| (11.3.12) |
Тогда динамическая составляющая второго порядка  будет определяться из следующего уравнения
будет определяться из следующего уравнения
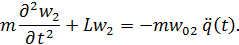
| (11.3.13) |
Представив вторую производную функции 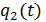 в виде непрерывных и разрывных составляющих по аналогии с (11.3.4), получим следующее уравнение для функций
в виде непрерывных и разрывных составляющих по аналогии с (11.3.4), получим следующее уравнение для функций 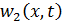

| (11.3.14) |
Здесь 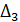 и
и  - скачки третьей и четвертой производных (11.3.2),
- скачки третьей и четвертой производных (11.3.2),  - непрерывная составляющая четвертой производной (11.3.5) функции
- непрерывная составляющая четвертой производной (11.3.5) функции  .
.
По аналогии с (11.3.7) представим решение 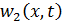 в виде суперпозиции двух функций
в виде суперпозиции двух функций
 , ,
| (11.3.15) |
где функции  и
и  определяются из решения следующих уравнений
определяются из решения следующих уравнений
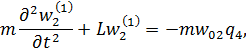
| (11.3.16) |

| (11.3.17) |
К уравнению (11.3.16) можно снова применить процедуру выделения квазистатической составляющей, отыскивая решение уравнения (11.3.16) в виде

| (11.3.18) |
Повторяя указанную процедуру n -1 раз, будем иметь

| (11.3.19) |
где  . .
| (11.3.20) |
Функция 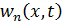 , динамическая составляющая n –го порядка, будет удовлетворять следующему уравнению
, динамическая составляющая n –го порядка, будет удовлетворять следующему уравнению
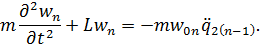
| (11.3.21) |
Производные первого и второго порядка от функции q 2( n -1) запишем в виде непрерывных и разрывных составляющих

| (11.3.22) |

|
представим функцию  в виде суперпозиции двух составляющих – от непрерывной правой части
в виде суперпозиции двух составляющих – от непрерывной правой части 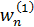 и разрывной
и разрывной 

| (11.3.23) |
Для определения указанных функций будем иметь следующие уравнения

| (11.3.24) |

| (11.3.25) |
Остановимся теперь на решении каждого из полученных в результате последовательного выделения квазистатической составляющей уравнений с непрерывной правой частью.
В правую часть каждого из уравнений входит в виде множителя функция  , получаемая из рекуррентной последовательности квазистатических уравнений, описанных в разделе 2.6.1.
, получаемая из рекуррентной последовательности квазистатических уравнений, описанных в разделе 2.6.1.
Решение уравнения типа (11.3.24) с непрерывной правой частью также было рассмотрено в предыдущем разделе и записывается следующим образом

| (11.3.26) |
где 
|
Как видно из (11.3.26), сходимость динамической составляющей n -го порядка от непрерывных правых частей после n кратного выделения квазистатики не ниже 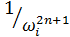 .
.
Остановимся теперь на решении динамических задач с правыми частями в виде дельта-функций и функций Хевисайда (11.3.9), (11.3.17), (11.3.25). Отыскивая решение уравнения (11.3.25) в виде разложения по собственным формам колебаний

| (11.3.27) |
и, учитывая выражение для коэффициентов Фурье  (11.2.23), получим следующее уравнение для обобщенных координат
(11.2.23), получим следующее уравнение для обобщенных координат

| (11.3.28) |
В правой части уравнения (11.3.28) в знаменателе стоит  , поэтому решение этого уравнения назовем реакцией на импульс и ступеньку n -го порядка.
, поэтому решение этого уравнения назовем реакцией на импульс и ступеньку n -го порядка.
При нулевых начальных данных решение уравнения (11.3.28) имеет вид

 . .
| (11.3.29) |
Подставив значения обобщенных координат (11.3.29) в (11.3.27), получим реакцию системы на импульс и ступеньку n -го порядка.
Проделанную в этом разделе процедуру последовательного выделения квазистатики и реакций системы на импульсы и ступеньки, соответствующие разрывам производных функций внешнего воздействия по времени, можно представить в виде следующей схемы (рис.2.1).
| w |
| w 1 |
| w 01 |
| w 01 |
| w 02 |
| w 0 n |
| w 2 |

|
| wn |

|
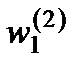
|

|

|
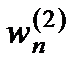
|

|
| q (t) |
| q 2(t) |
| q 2(n -1)(t) |
Рис. 2.1.
Здесь двойными сплошными стрелками указаны очередные этапы выделения квазистатических составляющих  , а внизу под ними – множители
, а внизу под ними – множители  с которыми они входят в суммарную функцию перемещения
с которыми они входят в суммарную функцию перемещения  . Штриховыми стрелками отмечены этапы выделения реакций на импульсные и ступенчатые внешние воздействия соответствующего порядка
. Штриховыми стрелками отмечены этапы выделения реакций на импульсные и ступенчатые внешние воздействия соответствующего порядка  .
.
Результирующее решение после n кратного выделения квазистатики и реакций системы на импульсы и ступеньки запишется так
  . .
| (11.3.30) |
Подставив в (11.3.30) значения функций 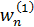 и
и  из (11.3.26), (11.3.27), получим следующее окончательное выражение для перемещения с учетом n ‑кратного выделения квазистатики в случае разрывных производных по времени функции внешнего воздействия.
из (11.3.26), (11.3.27), получим следующее окончательное выражение для перемещения с учетом n ‑кратного выделения квазистатики в случае разрывных производных по времени функции внешнего воздействия.


| (11.3.31) |
Из выражения (11.3.31) видно, что разрыв нечетных производных функций  вызывает реакцию системы, аналогичную той, которая возникает от импульсного воздействия. При этом в случае разрыва (2n–1)-ой производной со скачком
вызывает реакцию системы, аналогичную той, которая возникает от импульсного воздействия. При этом в случае разрыва (2n–1)-ой производной со скачком  сходимость решения не ниже
сходимость решения не ниже  . Разрыв четных производных функций
. Разрыв четных производных функций  вызывает реакцию, аналогичную возникающей при ступенчатом воздействии n -го порядка. При разрыве 2n-ой производной со скачкам
вызывает реакцию, аналогичную возникающей при ступенчатом воздействии n -го порядка. При разрыве 2n-ой производной со скачкам 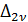 сходимость решения будет не ниже
сходимость решения будет не ниже  .
.
Таким образом, в представлении (11.3.31) квазистатическая составляющая (первое слагаемое) определяет разрывы и особенности динамической задачи в координатной области, тогда как третье слагаемое характеризует особенности решения типа реакций системы на импульсные и ступенчатые воздействия, обусловленные разрывом производных внешних сил во временной области. Выделение указанных составляющих из динамической задачи улучшает сходимость остающейся части решения (второго слагаемого) по формам собственных колебаний.