продольное нагружение однородного консольного стержня сосредоточенной силой
Проиллюстрируем влияние выделения квазистатики на сходимость решения в случае продольного нагружения однородного консольного стержня сосредоточенной силой, приложенной в среднем сечении.
Уравнение движения, а также граничные условия в этом случае имеют вид
| (11.4.1) |
Здесь EF - продольная жесткость, 2 l – длина стержня.
Начальные условия будем считать нулевыми. Функция 
изменяется по следующему закону, согласующемуся с нулевыми начальными данными
| (11.4.2) |
Будем искать решение задачи (11.4.1) в случае двукратного выделения квазистатики в соответствии с (11.2.1) в следующем виде
 .
| (11.4.3) |
Подставляя (11.4.3) в уравнение (11.4.1), получим равенство
 +
| (11.4.4) |
Здесь 
.
Отметим, что производные функции (11.4.2) до третьей включительно являются непрерывными функциями, а четвертая производная 
терпит разрыв в нуле
| (11.4.5) |
где 
– функция Хевисайда.
Из условия равенства нулю выражений, стоящих в скобках при и 
, в (11.4.4), определим функции 
и 
Для нахождения функци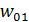й 
и 
получаем статические или в случае свободных краев квазистатические уравнения
| (11.4.6) |
Решения уравнений (11.4.6) с учетом граничных условий (11.4.1) имеют следующий вид
| (11.4.7) |
При выполнении условий (11.4.6) для динамической составляющей второго порядка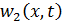 
из (11.4.4) получаем следующее уравнение
| (11.4.8) |
При этом в силу (11.4.3), (11.4.2) функция 
удовлетворяет нулевым начальным условиям
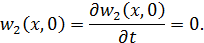
| (11.4.9) |
Будем отыскивать решение уравнения (11.4.8) в виде разложения по собственным формам колебаний консольного стержня
| (11.4.10) |
Частоты и формы колебаний консольного стержня имеют вид
| (11.4.12) |
Подставляя (11.4.10) в (11.4.8) и учитывая ортогональность собственных форм колебаний, для обобщенных координат получим следующее уравнение
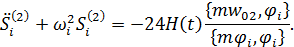
| (11.4.13) |
Вычислим с учетом (11.4.7) и (11.4.12) скалярные произведения, входящие в правые части уравнения (11.4.13)
| (11.4.14) |
Итак, уравнение (11.4.13) с учетом (11.4.14) принимает вид
| (11.4.15) |
Решение уравнения (11.4.15) с нулевыми начальными условиями запишется так
| (11.4.16) |
На основе формулы (11.4.3) с учетом (11.4.7), (11.4.10), (11.4.16), динамические перемещения стержня при двукратном выделении квазистатики примут вид
| (11.4.17) |
При прямом использовании метода разложения по собственным формам колебания без выделения квазистатики уравнения для обобщенных координат на основе (11.4.1) запишутся так
| (11.4.18) |
После интегрирования в (11.4.18) с учетом (11.4.2) получим следующее значение для динамического перемещения без выделения квазистатики
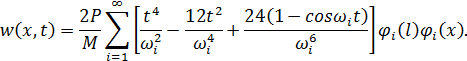
| (11.4.19) |
Путем разложения функци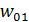й и (11.4.7) по формам колебаний (11.4.12) нетрудно убедиться, что правые части (11.4.17) и (11.4.19) равны.
Из сравнения рядов в (11.4.17) и (11.4.19) видно, что сходимость оставшейся динамической части решения в (11.4.17) после двукратного выделения квазистатики на четыре порядка по частоте выше сходимости решения, полученного путем прямого использования метода разложения по собственным формам колебаний.
поперечное нагружение шарнирно опертой балки сосредоточенным моментом
Рассмотрим поперечное нагружение шарнирно опертой балки сосредоточенным моментом, приложенным в среднем сечении балки длиной 2 l, и изменяющимся во времени по некоторому закону . С использованием дельта-функции 
представим сосредоточенный момент распределенным
|
Рассмотрим случай, когда изменяется по закону
 .
| (11.4.24) |
Уравнение поперечных колебаний однородной балки запишется так
| (11.4.25) |
Здесь 
- поперечное перемещение, 
и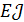 
- погонная масса и изгибная жесткость балки.
Граничные условия при шарнирном опирании краев имеют вид
| (11.4.26) |
Начальные условия будем считать нулевыми
| (11.4.27) |
Будем искать решение уравнения (11.4.25) с использованием однократного выделения квазистатической составляющей в виде
| (11.4.28) |
Функция 
при этом удовлетворяет следующему статическому уравнению
| (11.4.29) |
где 
| (11.4.30) |
Решение статической задачи (11.4.29) имеет вид
|
где 
.
Функция 
удовлетворяет модифицированному динамическому уравнению
| (11.4.31) |
Функци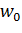и 
и 
удовлетворяют граничным условиям (11.4.26), а функция - с учетом (11.4.27) и (11.4.24) нулевым начальным условиям
Отыскивая решение модифицированного уравнения (11.4.31) путем разложения по формам собственных колебаний, придем к следующему уравнению для обобщенных координат
| (11.4.32) |
Собственные частоты и нормированные формы колебаний шарнирно опертой балки выражаются соотношениями
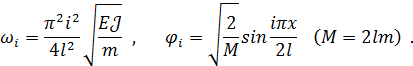
| (11.4.33) |
В силу соотношений (11.4.27) обобщенные координаты будут удовлетворять нулевым начальным условиям
коэффициенты Фурье статического решения 
, входящие в правую часть уравнения (11.4.32), в соответствии с (11.2.23) имеют вид
| (11.4.34) |
Двукратное дифференцирование функции 
(11.4.24) приводит к функции Хевисайда 
, поэтому уравнение для обобщенных координат (11.4.32) с учетом (11.4.34) примет вид
| (11.4.35) |
Решение уравнения (11.4.35) с нулевыми начальными данными запишется так
| (11.4.36) |
С учетом (11.4.36) придем к следующему выражению для чисто динамической составляющей
| (11.4.37) |
Итак, полное решение динамической задачи (11.4.25) с учетом (11.4.28) и (11.4.37) полученное с выделением квазистатической составляющей, запишется так
| (11.4.38) |
При использовании метода разложения по собственным формам колебаний впрямую без выделения квазистатической составляющей решение динамической задачи (11.4.25) будет таким
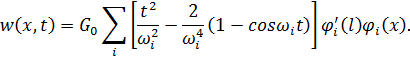
| (11.4.39) |
Если учесть зависимость собственных частот и форм колебаний от i 
, 
(11.4.33), то из сравнения (11.4.38) и (11.4.39) следует, что сходимость перемещений по тонам колебаний в случае выделения квазистатической составляющей имеет порядок 
, а без выделения квазистатики 
.
Определим изгибающие моменты 
на основе выражений для перемещений (11.4.38) и (11.4.39).
В случае выделения квазистатической составляющей (11.4.38) изгибающий момент запишется так
| (11.4.40) |
Без выделения квазистатики на основе (11.4.39) изгибающий момент примет вид
| (11.4.41) |
Нетрудно убедиться, что первая сумма в (11.4.41) представляет собой разложение в ряд Фурье квазистатического момента 
(11.4.30) по формам собственных колебаний (11.4.33).
Отметим, что ряд (11.4.41) характеризуется очень медленной сходимостью. Особенно сходимость ухудшается в окрестности скачкообразного изменения момента 
.
Поэтому формула (11.4.40), полученная на основе выделения квазистатической составляющей, является предпочтительной, так как она позволяет точно вычислить скачок изгибающего момента в точке x=l.
Укажем также на то, что ряд для перерезывающей силы, полученный без выделения квазистатики на основе формального дифференцирования изгибающего момента (11.4.41), является расходящимся.
Объясняется это тем, что базис собственных форм колебаний, полученный без учета инерции вращения, является неполным (смотри по этому поводу исследование, представленное в […]).
Формула для изгибающего момента (11.4.40), полученная с учетом выделения квазистатики, допускает дифференцирование и выражение для перерезывающей силы сходится как 1/ i 4.
| (11.4.42) |
столь сильное влияние выделения квазистатической составляющей на сходимость решения связано с тем, что фундаментальные решения динамических задач обладают одинаковыми особенностями или главными частями со статическими в пространстве координат [….]. Поэтому выделение из динамической задачи соответствующего квазистатического решения устраняет особенности и разрывы комбинаций производных, через которые выражаются кинематические и силовые факторы, и делает остающуюся часть динамического решения более гладкой и быстросходящейся. Особенно явно этот эффект прослеживается при наличии скачков во внешних нагрузках и при действии сосредоточенных сил.
Факт совпадения особенностей статических и динамических задач использовался при сведении граничных задач стационарных колебаний к интегральным уравнениям [……] (путем выделения особенностей статической задачи и построения комбинаций специальных функций, удовлетворяющих динамической задаче, с теми же особенностями).