В общем случае задача о динамическом нагружении некоторой упругой системы сводится к решению дифференциального уравнения
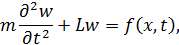
| (11.1.1) |
где 
и 
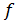- векторы кинематических параметров и внешних силовых воздействи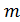й; 
и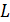 
– матрица масс и матричный оператор, характеризующий упругие свойства системы.
К уравнению (11.1.1) присоединяются начальные и граничные условия, и затем путем применения соответствующих дифференциальных операторов N к вектору w получают силовые факторы в сечениях конструкции.
Очевидно, что матрица m и матричные операторы L и N зависят от используемой при решении динамической задачи расчетной модели.
Рассмотрим наиболее распространенный случай, когда внешнюю силу 
в уравнении (11.1.1) можно представить в виде
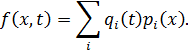
| (11.1.2) |
Более общий случай функции может быть сведен к (11.1.2) путем разложения функции в ряд по некоторой полной системе координатных функций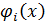 
.
В силу допустимости суперпозиции при решении линейной задачи (11.1.1) достаточно рассмотреть случай
 .
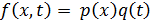| (11.1.3) |
При использовании традиционного метода разложения по собственным тонам колебаний без выделения квазистатики имеем
| (11.1.4) |
где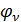 
– формы колебаний соответствующей задачи
 =1.
| (11.1.5) |
Обобщенные координаты Sj удовлетворяют уравнениям
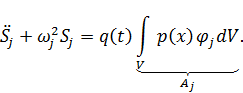
| (11.1.6) |
Интегрирование ведётся по области V, занимаемой системой.
Решение уравнения (11.1.6) для обобщенных координат 
с нулевыми начальными условиями записываются в квадратурах.
Отметим, что основная проблема связана со сходимостью вынужденной части решения из-за возможного действия на конструкцию сосредоточенных или разрывных внешних сил и моментов.
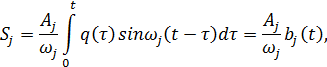
| (11.1.7) |
здесь
| (11.1.8) |
Общее решение (11.1.1) без выделения квазистатики будет иметь вид
| (11.1.9) |
При однократном выделении квазистатической составляющей решение уравнения (11.1.1) ищется в виде
 .
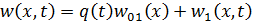| (11.1.10) |
Подставляем представление (11.1.10) в уравнение (11.1.1)
 .
|
Потребуем, чтобы функция 
удовлетворяла статическому уравнению
 .
| (11.1.11) |
Тогда динамическая составляющая 
будет удовлетворять следующему уравнению
| (11.1.12) |
При этом будем считать, что 
дважды дифференцируемая функция.
Для решения уравнения (11.1.12) также воспользуемся методом разложения по собственным тонам колебаний
| (11.1.13) |
Уравнение для обобщенных координат 
примет вид
| (11.1.14) |
Решение этого уравнения запишется так
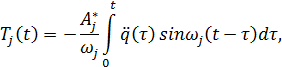
| (11.1.15) |
где
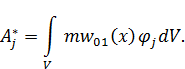
| (11.1.16) |
Коэффициенты 
, входящие в (11.1.15), по существу являются коэффициентами Фурье разложения статического решения 
.
Определим эти коэффициенты из решения уравнения (11.1.11). Будем отыскивать решение уравнения (11.1.11) в виде разложения по тонам колебаний
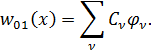
| (11.1.17) |
Подставив (11.1.17) в (11.1.11) получим
| (11.1.18) |
или с учетом (11.1.5)
| (11.1.19) |
Умножая (11.1.19) скалярно на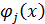 
, с учётом ортогональности форм колебаний и принятых обозначений (11.1.8) будем иметь
| (11.1.20) |
Окончательно выражение для разложения статической функции по тонам колебаний примет вид
| (11.1.21) |
Подставив представление для из (11.1.21) в (11.1.16), в силу ортогональности форм колебаний 
получим
| (11.1.22) |
При этом выражения для обобщенных координат (11.1.15) примет вид
| (11.1.23) |
где
| (11.1.24) |
Окончательно решение уравнения (11.1.1) с учетом однократного выделения квазистатической составляющей примет вид
| (11.1.25) |
Из сопоставления функций (11.1.9) и (11.1.25) видно, что однократное выделение квазистатики улучшает сходимость рядов по тонам колебаний на 
.