Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго.
Отношением отрезков 
и 
называется отношение их длин, т. е. 
.
Отрезки 
и 
пропорциональны отрезкам 
и 
, если 
.
Фигуры одинаковой формы называют подобными.
Стороны и 
, 
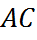и 
, 
и 
называются сходственными.
Подобными называются треугольники, у которых углы соответственно равны, а сходственные стороны пропорциональны.
Число 
, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Признаки подобия треугольников
Первый признак подобия треугольников:
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Прямая, параллельная одной из сторон треугольника, отсекает от него треугольник, подобный данному.
Прямоугольные треугольники подобны по острому углу.
Второй признак подобия треугольников:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между ними равны, то такие треугольники подобны.
Третий признак подобия треугольников:
Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Применение подобия к доказательству теорем и решению задач
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
Теорема.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 
, считая от вершины.
Отрезок 
называется средним пропорциональным (или средним геометрическим) для отрезков и , если 
.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла.
Соотношения между сторонами и углами прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного
треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
