Оглавление
Введение
Глава 1. Теория узлов
1.1 История развития и возникновения узлов
1.2 Понятие узлов
1.3 Теорема об узлах
1.4 Движения Рейдемейстера
Глава 2. Теория кос
2.1 История развития и возникновения кос
2.2 Понятие кос
2.3 Определение группы кос
2.4 Образующие группы кос
2.5 Связь между узлами и косами
2.6 Теорема Александера
Глава 3.Алгебра кос и узлов
3.1 Теорема Артина
3.2 Представление Бурау
Заключение
Список используемых источников и литературы
Введение
Данная работа посвящена исследованиям, лежащим в области геометрии, и касается изучения кос и узлов. Актуальность темы заключается в том, мы провели исследование на замечательную связь между двумя красивыми топологическими объектами: косами и узлами с которыми часто сталкиваемся в повседневной жизни, но не придаем этому значения. Что такое коса в математике? Грубо говоря, это формальная модель того, что понимается под словом «коса» или «сплетение» в обычной жизни (девичья коса, плетеный брелок, собачий поводок, сплетенный из кожаных полос, классический канат из переплетенных жил и т. д.), т. е. множество нитей, запутанных некоторым определенным образом. Цель курсовой работы заключается в глубоком изучении связи между теорией кос и теорией узлов.
Для осуществления обозначенной цели служат следующие задачи:
1. изучить теорию кос, историю возникновения и развития;
2. изучить теорию узлов, историю возникновения и развития;
3. изучить теорему Артина и представление Бурау.
Глава 1. Теория узлов
История развития и возникновения узлов
Узел галстука, узлы корабелов и альпинистов, гордиев узел, клубок змей, петля палача... Узлы — это и обиходные предметы, и символы сложности. Узлы — точнее, математическая теория узлов — интересует многих биологов, химиков, физиков. Узлы повсеместно использовались уже со времен античности. Это объясняется их важной технологической ролью, особенно в мореходстве и строительстве. Но появление веревок и узлов произошло раньше, в доисторические времена, и предшествовало изобретению топора, лука, колеса.
Сегодня мы применяем узлы, даже не задумываясь, что их возраст исчисляется тысячелетиями. Такие узлы, как выбленочный, прямой и беседочный (рис.1), служили жителям Древнего Египта еще пять тысячелетий назад.
Например, выбленочный узел был обнаружен на двери третьего помещения гробницы фараона Тутанхамона.
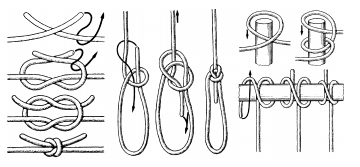
Рис.1
Прямой (или квадратный) узел, хорошо известный в Древнем Египте, был широко распространен в быту древних греков и римлян.
Лучшие из узлов пережили века, переходя от поколения к поколению. Существует изображения более 700 различных узлов.
Теорией узлов занимались не только математики. Большая заслуга принадлежит здесь физикам – начиная от лорда Кельвина, предложившего описывать химические элементы узлами, и кончая Э. Виттеном – единственным физиком – лауреатом филдсовской медали. Многие инварианты узлов (полином Джонса, а также инварианты конечного порядка, называемые также инвариантами Васильева) физики пытаются использовать в своих исследованиях.
Понятие узлов.
Узел - это некая абстракция, которая рассматривается не как веревка и шнур, а как бесконечно тонкая, гибкая и растяжимая нить. При рассмотрении математического узла нужно либо как-то зафиксировать его концы, либо соединить их.
Самый простой узел – тривиальный. Тривиальный узел может быть представлен как граница диска, гладко вложенного в R3. Узел называется нетривиальным, если он не эквивалентен тривиальному, т.е. его нельзя «пошевелить».
Есть много видов нетривиальных узлов, например, узел на рис.2 называется трилистником, узел на рис.3 – восьмеркой.

Рис.2 Рис.3
Дадим определение эквивалентности узлов. Узел – это ломаная. С ломаной можно производить элементарные операции: (рис.4)
1) два последовательных звена АВ и ВС ломаной заменить звеном АС;
2) звено АС заменить двузвенной ломаной АВUВС

Рис.4
Обе операции разрешены, если только треугольник АВС не пересекается (в пространстве) ни с какими другими кусками нашего узла.
Два узла называются эквивалентными, если их можно элементарными операциями превратить в совершенно одинаковые узлы.
Деформируя объемлющее пространство R3 мы также деформируем и узел. Два узла называются изотопными, если один из них может быть продеформирован в другой посредством диффеоморфизма объемлющего пространства на себя, сохраняющего ориентацию.
Для того чтобы показать, что два узла не являются изотопными, достаточно найти инвариант узлов, который принимает разные значения на этих узлах.
Узлы кодируются следующим образом. Сначала фиксируем узел, т.е образ отображения. Рассматривает некоторую плоскость и проекцию узла на нее. Без ограничения общности можно считать, что проекция узла на плоскость представляет собой вложенный конечный четырехвалентный граф, который является образом гладкого погружения окружности в плоскость. Часть этого узла называется ветвью. Каждая вершина графа проекции, которая называется перекрестком, оснащена структурой. Пусть a и b – две ветви узла, проекции которых пересекаются в какой-либо точке. Так как a и b не пересекаются в плоскости, то два прообраза этой точки имеют различные координаты. Таким образом, мы можем сказать, какая ветвь проходит сверху, т.е. образует переход, а какая – снизу, т. е. образует проход. Ребра переходов изображаются сплошными линиями, а ребра проходов имеют разрыв в перекрестке.(рис. 5)
Такое изображение узла называется плоской диаграммой узла.

Рис.5
Четырехвалентный граф проекции без указания структуры проходов и переходов называется тенью узла. Сложностью узла называется минимальное количество перекрестков диаграмм узлов.
У каждого узла есть зеркальное отражение, т.е. узел, полученный из него отражением в некоторой плоскости. Узел называется зеркальным, если он изотопен своему зеркальному отражению.
Теорема об узлах.
А можно ли умножать узлы? Если считать узлы кривыми, концы которых уходят в бесконечность, то произведение узлов a и b – это просто нить, на которой завязан сначала узел a, затем узел b.(рис.6)

Рис.6
Это умножение, как и умножение кос, ассоциативно: для любых узлов a,b и c
(a∙b)∙c=a∙(b∙c).
Тривиальный узел, т.е. вертикальная прямая является единичным элементом (рис.7)

Рис.7
В отличие от кос, ни один нетривиальный узел не имеет обратного: если мы завяжем на нити два узла, а затем потянем за концы, узлы не развяжутся.
Два узла, завязанных на одной веревке можно переставлять. Пусть на нити завязан сначала узел a, затем узел b (рис.8)

Рис.8
Не трогая узел a, «затянем» узел b в маленький узелок. (рис.9)

Рис.9
Потом заключим этот узелок в маленький стеклянный шарик и будем двигать его вверх по нити. (рис.10)

Рис.10
В итоге этот шарик окажется наверху, и его можно превратить опять в узел b. Таким образом, умножение узлов коммутативно:
a∙b=b∙a, отсюда следует теорема об узлах:
Узлы образуют ассоциативную и коммутативную систему относительно умножения. В этой системе есть единичный элемент, но нет обратных элементов.
Движения Рейдемейстера
Любая деформация плоскости, неизменяющая взаимное расположение перекрестков, не меняет изотопического типа зацепления. При этом существуют еще три движения, называемые движениями Рейдемейстера, которые обозначаются Ω1, Ω2, Ω3. Эти движения не изменяют расположение перекрестков и не меняют изотопического типа зацепления. (рис.11)
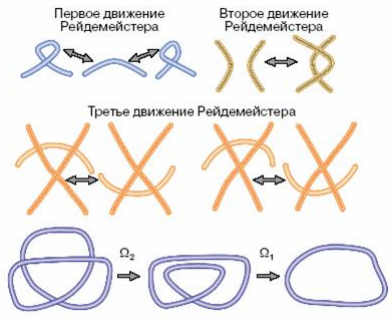
Рис.11
Каждое из трех движений Рейдемейстера изменяет диаграмму зацепления только внутри маленькой области. Это означает, что вне этой области диаграмма зацепления остается неизменной, а внутри изменяется так, как показано на рис.11 (сверху). Теперь можно показать, что узел, показанный на рис. 11 (снизу слева), тривиален.
Глава 2. Теория кос
История развития и возникновения кос
Коса – это какое-то количество нитей, которые переплетаются между собой.
Теория кос - наука, возникшая в 20-х годах 20-ого века. Исследования на эту тему еще не завершены.
Основания теории кос были построены благодаря азарту и настойчивости немецкого математика Эмиля Артина. Первоначально косы были предложены Артином в качестве математической модели для текстильной промышленности. Теория кос занимает важное место в комплексном анализе, комбинаторике, квантовой механике и квантовой теории поля.
Понятие кос
Математическая коса состоит из n нитей, т.е. кривых в пространстве, которые начинаются в n точках горизонтальной прямой и заканчиваются в n точках другой горизонтальной прямой, которая расположена ниже. Нити должны быть нисходящими, т. е. касательный вектор в какой-то точке кривой должен «смотреть вниз».
Можно получить узел из косы с помощью операции замыкания, которая состоит в том, чтобы присоединить верхние концы прядей к нижним концам (рис. 12 узел – трилистник)
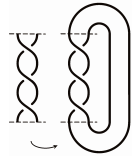
Рис.12
Рис. 13 показывает, что не всегда таким образом можно получить узел. Замыкание косы может также оказаться зацеплением, т. е. состоять из нескольких кусков (из нескольких кривых, в отличие от узла, по определению, состоящего лишь из одной кривой).

Рис.13
Какие узлы можно получить таким образом? Ответ, полученный американским математиком Александером в 1923 г.,объясняет важность кос в теории узлов: можно получить любой узел!
Теорема Александера:
Каждый узел может быть получен как замыкание некоторой косы.
(Фактически Александер показал, что это утверждение верно для зацеплений, частным случаем которых являются узлы.) Вероятно, Александер надеялся, что его теорема послужит решающим шагом классификации узлов. Действительно, косы являются значительно более простыми объектами, чем узлы; множество кос обладает весьма прозрачной алгебраической структурой, позволяющей их классифицировать.
Следовательно, мы можем получить классификацию узлов, основываясь на классификации кос.
Вернемся к изучению кос. Прежде всего мы определим операцию произведения на множестве кос c одним и тем же количеством нитей n.
Эта операция заключается в последовательном связывании кос (соединении верхних концов нитей второй косы с нижними концами нитей первой), как на рис.14.

Рис.14
Сейчас мы убедимся, что произведение кос обладает многими свойствами обычного произведения чисел. Прежде всего, имеется единичная коса (обозначаемая e), т. е. коса, которая, как число 1, не изменяет то, что на нее умножается. Это тривиальная коса, нити которой спадают вертикально, не переплетаясь. Действительно, прикрепление снизу тривиальной косы к данной косе приводит лишь к удлинению ее нитей и не изменяет тип косы.
Во-вторых, для каждой косы b существует коса, называемая обратной 1-и обозначаемая b, такая, что ее произведение с b дает тривиальную косу,
b · 1- b = e (так же как для каждого числа n его произведение с обратным числом 1/n, равно единице.)
Эта коса получается, если взять отражение данной косы в горизонтальном зеркале.
Действительно, каждый перекресток уничтожается своим зеркальным изображением, таким образом, все перекрестки взаимно уничтожаются попарно шаг за шагом, начиная с середины косы-произведения.(рис.15)

Рис.15
Третье свойство, общее у кос и у чисел, — свойство ассоциативности произведения: всегда выполняется равенство (a · b) · c = a · (b · c).
Когда некоторое множество снабжено операцией, обладающей тремя свойствами, то это и есть группа.
Следовательно, множество кос с n нитями образует группу. Эту группу мы будем обозначать через Bn.
Отметим сразу же, что группа кос Bn (для n > 2) — в отличие от чисел — не коммутативна: произведение двух кос зависит в общем случае от порядка множителей.
Существование произведения кос позволяет заменять рисунок, изображающий косу, некоторым словом — алгебраическим представлением этой косы.
Действительно, двигаясь сверху вниз вдоль косы, наша коса — последовательное произведение кос с одним перекрестком в каждой (рис. 16); они называются элементарными косами и обозначаются (в случае кос с n нитями) - b1,b2,…,bn-1.
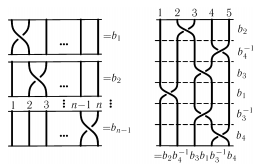
Рис.16
Между косами существует отношение эквивалентности (изотопия).
Определения группы кос