Узлы, как и косы интересно рассматривать с точностью до изотопии (для ориентированных узлов требуют, чтобы изотопия сохраняла ориентацию), т.е. до сохраняющих ориентацию деформаций пространства на себя.
При таких деформациях окружность может растягиваться, но не может разрываться и склеиваться (самопересекаться). Как и в случае кос, такие движения называются изотопиями.
Можно спроектировать узел на некоторую плоскость, которую можно добиться малым шевелением, проекция узла будет представлять собой плоскую кривую, все точки самопересечения которой являются двойными, причем в каждой точке самопересечения указано, где узел идет выше, а где - ниже (переход и проход). При этом понятия «выше» и «ниже» определяются следующим образом.
Без ограничения общности можно считать, что плоскостью проекции является плоскость Oxy со стандартной ориентацией. В этом случае нить проходит «выше», если она имеет большую координату z в прообразе точки пересечения и ниже в противном случае. Такая диаграмма называется плоской диаграммой узла.
Аналогично узлам можно рассматривать зацепления, которые представляют собой набор непересекающихся несамопересекающихся окружностей в трехмерном пространстве. Каждая из этих окружностей представляет собой узел, который называется компонентой зацепления.
Для зацеплений также можно рассматривать плоские диаграммы с проходами и переходами. Каждое зацепление можно ориентировать, для этого нужно задать направление обхода каждой его компоненты. В таком случае говорят об ориентированных зацеплениях (узлах).
Тривиальным узлом называется узел в трехмерном пространстве, изотопный узлу, допускающему плоскую диаграмму без перекрестков.
Тривиальное зацепление из n компонент - это зацепление, каждая компонента которого является тривиальным узлом, причем трехмерное пространство можно разделить на непересекающиеся между собой области, так чтобы каждая компонента лежала в своей области.
Тривиальное зацепление изотопно зацеплению, имеющему плоскую диаграмму без перекрестков, состоящую из непересекающихся окружностей.
Связь между теорией кос и теорией узлов - похожесть способов их изображения.
Рассмотрим некоторую плоскую диаграмму некоторой косы из n нитей. У этой диаграммы помимо проходов и переходов есть еще свободные концы - по n штук сверху и снизу. Эти концы можно замкнуть, соединяя каждый конец сверху с нижним концом косы, имеющим ту же абсциссу, при этом не создавая лишних перекрестков. (рис. 20)

Рис.20
Мы получили диаграмму узла или зацепления. Это зацепление естественным образом ориентировано: мы ориентируем все нити косы сверху вниз и далее продолжаем ориентацию на замыкание.
Если две косы являются изотопными, то и соответствующие им зацепления также являются изотопными.
Теорема Александера
Теорема Александера формулируется так: «Каждый узел может быть получен как замыкание некоторой косы».
Заметим, что искомая коса моментально находится, если узел является обмоткой, т. е. если он закручивается в одном и том же направлении вокруг некоторой точки. (рис. 21)

Рис.21
Действительно, для этого достаточно разрезать узел вдоль полупрямой, исходящей из центра, и затем развернуть его в косу. (рис. 22)
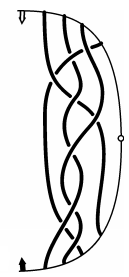
Рис.22
Если узел не является обмоткой, как, например, на рис. 23(а), то в этом случае достаточно заставить его «толстую» часть (показанную на рисунке более жирной линией), которая закручивается относительно точки C в «неправильном» направлении, пройти под точкой C с другой стороны кривой; тогда мы получим узел-обмотку (рис. 23(б)), который можно развернуть далее в косу, как в предыдущем примере (рис. 23(в))
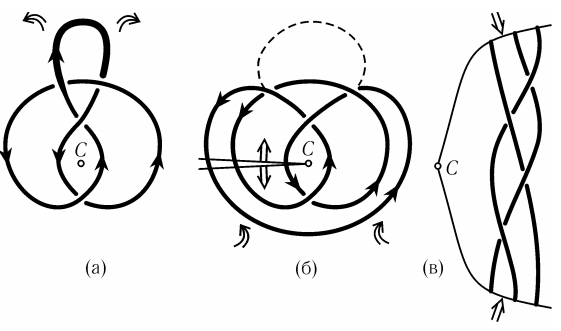
Рис.23
Фактически этот красивый прием (преобразование произвольного узла в узел-обмотку) является основным, и именно благодаря ему Александер сумел доказать свою теорему.
К недостаткам этого метода можно отнести отсутствие эффективности с практической точки зрения и его трудно реализовать на компьютере.