КУРСОВАЯ РАБОТА
Выполнил:
студент 3 курса очной/заочной формы обучения
Феофанова
Андрея
Сергеевича
Руководитель:
(уч. степень, уч. звание) __________________ Ф.И.О.
Итоговая оценка - ________________________________
Подпись______________________должность, уч. степень, уч. звание, Ф.И.О. руководителя
Коломна – 2017 г.
Оглавление
Введение……………………………………………………………………3
Глава 1. Решетка на плоскости……………………………………………4
§1. Понятие и определение решетки. Узлы………………………………5
§2. Свойства решетки на плоскости………………………………………6
Глава 2. Многоугольники…………………………………………………7
§1. Треугольник и квадрат…………………………………………………8
§2. Правильные многоугольники…………………………………………9
§3. Элементарные параллелограммы……………………………………10
Глава 3. Формула Пика…………………………………………………11
§1. Георг Пик. Жизнь и работа…………………………………………12
§2. Формула Пика для многоугольников. Её вывод……………………13
Заключение………………………………………………………………..15
Список литературы………………………………………………………16
Введение
Математические знания – вещь уникальная. Они копятся и систематизируются с древнейших времен, не теряя своей актуальности. Купцы, жрецы и простые городские жители в древности, а ныне продавцы, пловцы и мудрецы – жизнь для всех без математических навыков пуста. Начиналась наука с того, что имела самое практическое применение – измерять расстояния, площади, объёмы и т.д. На сегодняшний день, математика – обширнейшая область знаний, задействованная в любой другой науке и сфере жизни.
А жизнь каждого школьника начинается с листа бумаги в клетку. Но не один из первоклассников и представить себе не может, на что способен он с помощью простого листа бумаги в клетку, отчасти о котором пойдет речь в данной курсовой работе.
Листок в клетку – самый очевидный и важнейший пример точечной решётки. Мы на ней чертим, рисуем, выводим красивые и не очень геометрические фигуры. Эта самая простая решётка стала, например, для немецкого математика К.Гаусса отправной точкой в работе по сравнению площади круга с количеством точек с целыми координатами, находящимися внутри него. И вообще именно Гаусс стал основоположником использования целочисленной решётки. А другой немецкий математик с корнями из Российской Империи Г.Минковский заметил, что элементарные геометрические утверждения тесно связаны с арифметическими исследованиями. Он одним из первых, в 1896 году, для рассмотрения алгебраических проблем привлек методы геометрии.
Данная курсовая работа посвящена вопросам, которые находятся на границе арифметики и геометрии, и именно этим проблема исследования вызывает неподдельный интерес.
Какие из всех возможных правильных многоугольников можно расположить на решетке так, что все его вершины попадают на узлы решетки? Курсовая работа посвящена ответам на этот и некоторые другие вопросы. Например, для ответа на заданный вопрос на помощь приходит утверждение об иррациональности значений тригонометрических функций.
Также в этой работе будет показана формула австрийского математика Георга Пика, которая у каждого 11-классника вызывает радость, потому что сильно сокращает время выполнение планиметрического задания первой части ЕГЭ и уменьшает количество формул для нахождения площадей, которые приходится запоминать.
Как оказывается, решётка на плоскости, о которой пойдёт речь, является мощнейшим средством, позволяющим алгебраические задачи решать на геометрическом языке и наоборот. Это движение по мосту между арифметикой и геометрией является, как будет показано, двусторонним и достаточно интенсивным.
Цели курсовой работы:
− обоснование связи между арифметикой и геометрий;
− обобщение научных знаний по теме «Многоугольники на решётке».
Задачи курсовой работы:
− систематизировать знания, находящиеся на границе арифметики и геометрии;
− обосновать формулу Пика для правильных многоугольников;
− показать практическое применение формулы Пика.
Глава 1. Решётка на плоскости
Понятие и определение решётки. Узлы
Целочисленной решёткой, вообще говоря, называется множество точек на прямоугольной (декартовой) координатной плоскости, имеющих целочисленные координаты. Легче всего представить решётку как бесконечный лист клетчатой бумаги (рис.1.1). Важно отметить, что многоугольник только тогда считается расположенным на целочисленной решётке, когда все его вершины являются точками этой решётки. Отметим, что точки также называются узлами решётки.
| Рисунок 1.1 |
Отметим, что в предыдущем абзаце речь идет о двумерной целочисленной решётке. А вообще, решётка может быть n-мерной. Она имеет своё обозначение: 
. В данной работе речь будет идти только о двумерной целочисленной решётке 
. Но общее определение целочисленной решётки, конечно, дадим. Целочисленная решётка – это совокупность точек плоскости (пространства), координаты которых в некоторой системе координат имеют целочисленные координаты.
Важную роль решётка играет не только в вопросах подсчёта площадей многоугольников, но и в теории функций, в теории чисел, в химии (в кристаллографии) и во многих других областях. При изучении симметрии также часто используется целочисленная решётка.
Есть целый раздел геометрии – геометрия чисел, которую создал немецкий математик Минковский, которого выше мы уже упоминали. Этот раздел математики получил широкое развитие в работах наших соотечественников: Г.Ф.Вороного, Б.Н.Делоне и многих других.
| Рисунок 1.2 |
Работа с листом в клетку восхищает, однако вполне возможно, что целочисленная решётка – это не только клетчатый лист. Это может быть и листок в треугольник. Его можно увидеть на рисунке 1.2. Иначе говоря, это треугольная решётка, точки пересечения которой, как и прежде, называются узлами.
Вполне может вызвать интерес такое маленькое исследование. А будет ли та же формула Пика, с которой мы ещё познакомимся, актуальна для треугольной решётки? Как окажется, формулы совпадут.
Далее речь пойдет о свойствах целочисленной решётки. Прежде чем о них говорить, нужно показать, каким образом вообще можно задать целочисленную решётку.
Рассмотрим на плоскости два семейства параллельных прямых, разбивающих плоскость на равные параллелограммы; множество L всех точек пересечения этих прямых (или множество вершин всех параллелограммов) и назовём точечной решеткой или простой решеткой, а сами точки – её узлами. Любой из этих параллелограммов называется фундаментальным параллелограммом или параллелограммом, порождающим решетку; площадь фундаментального параллелограмма решетки L обозначим через ∆=∆(L). Обычно предполагается, что начало координат является одним из узлов решетки.
Задать решетку можно еще следующим образом. Предположим, что на плоскости заданы две пересекающиеся прямые l0 и m0, а так же два положительных числа a и b. По обе стороны от прямой l0 проведем параллельные прямые l±1, l±2, l±3... отметим все точки пересечение прямых li с прямыми mj; множество всех этих точек пересечения и является решеткой L. (рис 2.1)
| Рисунок 2.1 |
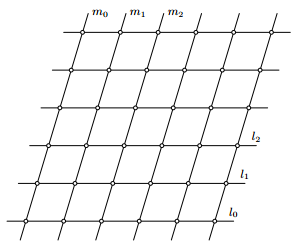Нужно иметь в виду, что решетка состоит из точек, а сами прямые к ней не относятся. Одна и та же решетка может быть получена при помощи различных семейств параллельных прямых.
| Рисунок 2.2 |
На рисунке 2.2 изображена так называемая ортогональная целочисленная решетка Z2, состоящая из точек с целыми координатами в декартовой (прямоугольной) системе координат. То же семейство точек можно получить пересечением других семейств прямых, не являющихся ортогональными. Таким образом, решётка точек напрямую не связана с семейством прямых в отличие от её фундаментального параллелограмма.
Также известен способ задания целочисленной решётки с помощью параллелограмма. Изначально отмечают вершины имеющегося параллелограмма, а затем начинают этот параллелограмм смещать параллельно одной из сторон. Длина смещения равна длина стороне, параллельно которой двигают фигуру. Этот процесс сначала происходит в одном направлении, затем – в противоположном. Таким образом, на плоскости образуется полоса, граница которой состоит из вершин параллелограмма – точек, которые и становятся узлами.
После начинают сдвигать имеющуюся полосу в направлении другой стороны параллелограмма. Ясно, что длина смещения равна длине стороны. Отмечают вновь получившиеся точки и представляют, что этот процесс происходит в двух противоположных направлениях. Таким образом, образуется решётка, имеющая целочисленные координаты. А параллелограмм, с которого было начато задание решётки, и называется фундаментальным, или, иначе говорят, что данный параллелограмм порождает эту решётку.
Это были рассмотрены основные способы задания решётки на плоскости. Но вначале было отмечено, что решетка может быть задана как в плоскости, так и в любом n-мерном пространстве. Для построения целочисленной решётки в 3-мерном пространстве используется произвольный параллелепипед.
Аналогично могут быть определены решётки в пространствах любой размерности.