А теперь самое интересное. Пришло время показать саму формулу Пика, доказать то, что она имеет право на существование и на нескольких примерах показать её применение.
Теорема. Для любого простого многоугольника P на целочисленной решётке имеет место формула: 
, где 
– число узлов решётки, расположенных строго внутри многоугольника, а 
– количество узлов решётки, расположенных строго на его границе (включая вершины).
| Рисунок 4.1 |
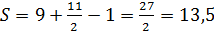. Если попытаться найти площадь данной фигуры с помощью обыкновенных школьных знаний, применив формулы площади треугольника, квадрата и другие известные ещё школьникам формулы, то получится такой же результат. В этом легко убедиться.
Перед доказательством также отметим, что любой простой многоугольник имеет, по крайней мере, одну диагональ, которая расположена целиком внутри многоугольника.
Отсюда из принципа математической индукции следует, что любой простой k-угольник можно разбить на (k-2) треугольника, все вершины которых являются вершинами исходного многоугольника и, в частности, узлами решётки. Поэтому сумма всех внутренних углов простого k-угольника равна (k-2)π.
Затем, каждый из полученных треугольников разобьём на примитивные треугольники. Как было сказано ранее, площадь каждого примитивного треугольника равна ½, поэтому число примитивных треугольников в разбиении равно 2*S. Следовательно, это никак не зависит от способа разбиения.
Чтобы доказать формулу Пика, нужно доказать также следующее равенство: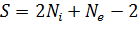 
. Нужно предположить, что P является k-угольником. Его вершины будут также и вершинами некоторых примитивных треугольников разбиения. Сумма углов треугольника при таких вершинах равна сумме внутренних углов многоугольника P и, тем самым, равна 
.
| Рисунок 4.2 |
Узел решётки, который находится на границе P, но не является его вершиной, также участвует в разбиении и служит вершиной некоторых примитивных треугольников, а сумма всех углов при всех таких вершинах-узлах равна
.
Каждая из точек решётки (находящихся внутри P) участвует в разбиении на примитивные треугольники и является их вершинами. Сумма углов, сходящихся в одной точке, равна 360 
. Поэтому сумма всех углов всех примитивных треугольников с вершинами во внутренних узлах равна 360 
.
С другой стороны, сумма углов всех примитивных треугольников равна 180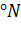 
и поэтому: 
.
Следовательно, 
. Тем самым, теорема Пика доказана.
Необходимо сделать замечание. Пусть плоскость разбита на равные параллелограммы двумя семействами параллельных прямых, как мы делали это, когда учились задавать целочисленную решётку. Ещё легче, если представить себе «косоугольную» клетчатую бумагу». Тогда вершины параллелограммов образуют множество, которое называется точечной решёткой. Так вот формула Пика на произвольной точечной решётке будет также справедлива. Только необходимо всё выражение домножить на площадь каждого из параллелограммов. Доказательство будет проводиться тем же способом.
Существует множество утверждений для подсчёта площади как треугольников, так и для многоугольников, но формула Пика для всех других формул является самым сильным утверждением.
Как не раз было отмечено, формула Пика имеет широкое применение на практике. Приводим несколько интересных задач, для решения которых формула Пика будет очень полезна.
1) Шахматный король обошел доску 8 × 8 клеток, побывав на каждом поле ровно один раз и последним ходом вернувшись на исходное поле. Ломаная, соединяющая последовательно центры полей, которые проходил король, не имеет самопересечений. Какую площадь может ограничивать эта ломаная? (Сторона клетки равна 1.)
Из формулы Пика сразу следует, что площадь, ограниченная ломаной, равна 64/2 − 1 = 31. Здесь узлами решетки служат центры 64 полей и, по условию, все они лежат на границе многоугольника. Таким образом, хотя таких «траекторий» короля достаточно много, но все они ограничивают многоугольники равных площадей.
2) Середины сторон квадрата соединены отрезками с вершинами так, как это показано на рис. 4.3. Найти отношение площади квадрата к площади восьмиугольника, образованного проведенными отрезками.
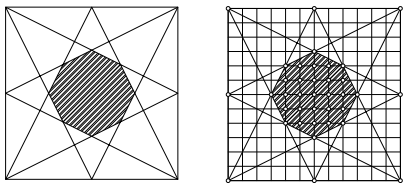
Довольно стандартная и распространенная ошибка при решении этой задачи состоит в предположении, что «из симметричности ситуации следует, что восьмиугольник правильный». Однако это не так: он равносторонний, но углы у него не равны. Так как нам нужно найти отношение площадей, то размеры квадрата для нас роли не играют. Поэтому рассмотрим квадрат, расположенный на целочисленной решетке Z 2, размером 12 × 12; стороны квадрата лежат на прямых решетки. Тогда, как нетрудно заметить, все вершины восьмиугольника являются узлами решетки; более того, отсюда легко заметить, что этот восьми- угольник правильным не является (рис. 4.3) — он равносторонний, но не равноугольный. Из формулы Пика теперь легко следует, что площадь восьмиугольника равна 21 + 8/2 − 1 = 24. Поэтому искомое отношение площадей равно 6.
| Рисунок 4.3 |
Заметим, что если бы вместо квадрата мы взяли параллелограмм, то решение не изменилось бы.
Таким образом, показано, что формула Пика популярна при решении самых обыкновенных задач.
Заключение
Как было написано в одной интересной математической книге, мир математики кажется сложным и неизведанным для того, кто даже не попытается снять с двери в мир математики замок. Замок, который всем своим видом показывает, что вам тут делать нечего. А это вовсе не так. На примере не самой простой теме мы показали, что мир математики интересен и познавателен.
В нём есть множество загадок, которые учёные по всему миру пытаются разгадать день за днём и неделю за неделей.
Нынешняя математика – это настоящий синтез математических дисциплин, которые, на первый взгляд, кажутся абсолютно несвязанными между собой. Например, формула Пика, как не раз было отмечено в данной курсовой работе, это синтез арифметики, геометрии и алгебры. А возможен этот синтез стал благодаря работе множества учёных. Особенное место занимает Георг Пик, которому был посвящён целый параграф.
Формула Пика имеет самое практическое применение на сегодняшний день. Она может быть полезна как выпускникам школ, так и студентам высших учебных заведений.
Познавайте математику и делайте мир вокруг лучше!
Список использованной литературы
1. Многоугольники и многогранники // Энциклопедия элементарной математики. Т. 4. — М.: Физматгиз, 1963.
2. В а с и л ь е в Н. Б. Вокруг формулы Пика // Квант. — 1974. — № 12. C. 39–43.
3. МНОГОУГОЛЬНИКИ НА РЕШЕТКАХ//В.В.Вавилов, А.В.Устинов// Москва Издательство МЦНМО 2006
4. Алгебра и арифметика элементарных параллелограммов//Андрей Леонидович Канунников//статья «механико-математический факультет МГУ», 2006г.