Свойства решетки на плоскости

Теперь отметим ряд простейших свойств решёток.

1) Прямая, проходящая через 2 узла решётки, содержит бесконечное количество узлов. При этом все расстояния между двумя соседними узлами, лежащими на этой прямой, равны между собой.

2) Преобразование параллельного переноса плоскости (пространства), переводящего один узел решётки в другой её узел, переводит решётку саму в себя.

3) Решётка центрально-симметрична относительно середины любого отрезка, который соединяет два узла этой решётки. Более того, середины всех отрезков с концами в узлах данной решётки образуют новую решётку, включающую старую.

Первые три свойства кажутся достаточно очевидными, потому что все они вытекают из способа задания решётки. Их доказательство строится на основе способа задания.

4) Правило параллелограмма: Если три вершины параллелограмма являются узлами решётки, то и четвёртая его вершина – также узел решётки. В пространстве: если четыре вершины параллелепипеда, не лежащие в одной плоскости, являются узлами решётки, то и остальные его вершины – тоже узлы решётки.

Рисунок 2.3

Для доказательства этого свойства предположим, что ABCD — параллелограмм и точки A, B, C принадлежат решетке L. Мы должны доказать, что точка D лежит на пересечении двух прямых из каких- то различных семейств параллельных прямых, которые определяют эту решетку. Точки A, B и C — узлы решетки, поэтому они лежат на некоторых параллельных прямых p, q и r из одного семейства (рис. 2.3). (Если p=q, то доказательство очевидно.)

Из точки A опустим перпендикуляр AQ на прямую q, а из точки D — перпендикуляр DR на прямую r. Треугольники ABQ и DCR подобны, так как их стороны соответственно параллельны. Но AB=CD, значит, эти треугольники равны; следовательно, AQ=DR. Это означает, что прямая, проходящая через точку D и параллельная прямой r, принадлежит тому же семейству параллельных прямых, которому принадлежат прямые p, q, r. Таким образом, D лежит на прямой одного из двух семейств параллельных прямых, определяющих решетку. Аналогично показывается, что точка D лежит также и на прямой из другого семейства параллельных прямых, определяющих решетку. Значит, свойство доказано.

5) Если параллелограмм с вершинами в узлах решётки не содержит других узлов на сторонах и внутри себя, то он эту решётку порождает, то есть является её фундаментальным параллелограммом. Важно отметить, что данное свойство является критерием того, что параллелограмм является фундаментальным.

Для доказательства заключительного свойства заметим следующее. Если вершины параллелограмма являются узлами решётки, а сам параллелограмм содержит какой-либо другой узел решётки внутри себя или на сторонах, то он не может порождать эту решётку. Причина в том, что сдвигая его для построения решётки, мы «пропустим» узлы исходной решётки.

Пусть теперь параллелограмм P = ABCD не содержит никаких других узлов данной решетки L, кроме своих вершин. Начиная с P, построим решётку L’. Нужно показать, что L=L’.

Ясно, что решетка L’ содержится в L. Предположим, что существует такой узел E решетки L, который не является узлом решетки L’. Так как параллелограмм P порождает решетку, то вся плоскость покрыта равными параллелограммами, и поэтому точка E лежит внутри некоторого параллелограмма P’ = A’B’C’D’ или на его сторонах; при этом стороны параллелограмма P’ параллельны соответствующим сторонам параллелограмма P (рис. 2.4). Параллельный перенос на вектор 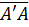переводит (по свойству 2) обе решетки сами в себя.

Рисунок 2.4

Но тогда узел E перейдет в некоторый узел решетки L, который будет расположен внутри или на сторонах параллелограмма P, чего быть не может по сделанному предположению.

Из всего вышесказанного следует, что свойство 5 имеет место быть.

 

 

Глава 2. Многоугольники

Прежде чем вывести и обосновать формулу Пика, вспомним, что многоугольник – это геометрическая фигуру, которую чаще всего определяют как замкнутую ломаную без самопересечений. Однако иногда самопересечения допускаются, но в таком случае многоугольник не является простым. В этой главе мы рассмотрим самые основные виды многоугольников, а точнее то, какие из них можно расположить на решётке, и что хорошего это несёт за собой при изучении геометрии.

Стоит отметить, что в дальнейшем часто будет использоваться выражение «расположен на какой-либо решётке ». Нужно понимать, это означает, что все вершины данного многоугольника совпадают с узлами этой решётки.

Треугольник и квадрат

Первое, о чем будет сказано в данном параграфе, это весьма интересный факт, который впервые по некоторым данным доказал французский математик Ф.Лукас в 1878 году. Доказательство этого факта производится на основе элементарных знаний по делимости чисел.

Теорема. Правильный треугольник нельзя расположить на целочисленной решётке .

Утверждение кажется, на первый взгляд, очень сомнительным, однако, если попытаться такой треугольник изобразить на клеточном листе, то это действительно окажется невозможным. А если уж и получится изобразить, то этот человек станет очевидным номинантом на премию Филдса.

Для доказательства воспользуемся методом «от противного». Предположим, что какой-либо правильный треугольник можно расположить на решетке нужным образом и что начало координат находится в одной из его вершин, а две другие его вершины имеют координаты (a, b) и (c, d). Можно считать, что четыре целых числа a, b, c, d не имеют общих делителей, отлич ных от ±1. Последнее следует из того, что точки (0, 0), (a/k, b/k), (c/k, d/k) также являются вершинами правильного треугольника, если k — общий делитель всех четырех чисел (рис. 3.1).

Рисунок 3.1

Так как , то отсюда заключаем, что .

Следовательно, , то есть сумма квадратов 4 целых чисел делится на 4. Но в таком случае все числа должны быть или чётные, или нечётные. Первое невозможно, так как вначале мы указали, что все эти числа должны быть взаимно просты. Случай с нечётными же числами невозможен, поскольку тогда не будет выполняться соотношение: , потому что его левая часть не делится на 4, а правая делится. Мы пришли к противоречию, которое и говорит о том, что сформулированное утверждение неверно, а значит, правильный треугольник действительно нельзя расположить на целочисленной решётке в самом широком понимании. Что и требовалось доказать.

Но этим доказательством не ограничивается количество вообще существующих способов доказательства. Можно доказать сформулированную теорему даже с помощью тригонометрии.

Рисунок 3.2

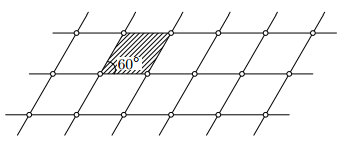
Итак, как мы поняли, решётка на плоскости не содержит правильный треугольник. Очевидным является тот факт, что решётка, о которой идёт речь, в свою очередь, может содержать квадрат. Но всякая ли плоская решётка может содержать квадрат? Например, на рисунке 3.2 достаточно очевидно, что решётка квадрат не содержит. Вопрос, содержит ли данная решётка правильный треугольник, оставим пока открытым, но здесь вполне уместным будет следующее утверждение, которое многое поясняет.

Теорема. Не существует плоской решетки, содержащей одновременно квадрат и правильный треугольник.

То есть нашу первую теорему о расположении правильного треугольника на решётке вполне можно рассматривать как следствие из последней теоремы. Потому что возможность расположения квадрата там очевидна, а следовательно, правильный треугольник задать не получится.

Рисунок 3.3

Решётка (обозначим её как L_t), которая приведена на рисунке 3.2 любопытнее чем кажется на первый взгляд. На неё стоит обратить особое внимание. Фундаментальным параллелограммом, который порождает данную решётку, является ромб с длиной стороны 1 и с острым углом 60 градусов. В ней и только в ней можно поместить прямоугольный треугольник. Подтверждение этого факта можно увидеть на рисунке 3.3. Но, что интересно, этот треугольник никогда не будет иметь целочисленные длины сторон. И в этом заключается следующее утверждение, на котором разговор о треугольниках на решётке будет закончен. Напомним, что треугольник называется пифагоровым, если он имеет целочисленные длины сторон.

Теорема. Никакой пифагоров треугольник нельзя расположить на решетке L_t.

Теперь пришло время перейти к правильным многоугольникам.