Математическое творчество Архимеда.

КУРСОВАЯ РАБОТА

 

Выполнила:

студентка 3 курса очной формы обучения

Сергеева Екатерина Александровна

 

 

Руководитель:

Кфмн,доцент Кирин Н.А

 

Итоговая оценка - ______________

Подпись______________________

 

Коломна 2017г

Содержание

Введение…………………………………………………………………………...3

Глава 1. Задачи Античности

1. Математическое творчество Архимеда.………………………………………4

2. Задача Иосифа Флавия…………………………………………………..........14

Глава 2. Задачи Средневековья

1. Вклад Омара Хайама …………………………………………………………23

2. Задача Фибоначчи Леонардо Пизанского и его вклад в развитие математики.………………………………………………………………………26

Заключение………………………………………………………………….........33

Список литературы………………………………………………………………34

Введение

В данной работе моей задачей является изучение задач Античности и Средневековья, а целью считаю выявление их влияния на развитие математики.

Выбранная тема актуальна, так как с помощью нее можно узнать историческую основу математики.

Глава 1. Задачи Античности

 

Математическое творчество Архимеда.

От Архимеда до нас дошли десять сравнительно крупных и несколько более мелких сочинений, в основном математического характера: "О шаре и цилиндре", "Измерение круга", "О коноидах и сфероидах", "О спиралях", "Квадратура параболы", "Исчисление песка", "Послание Эратосфену". Кроме того, два сочинения, примыкающих по содержанию к механике: "О равновесии плоскостей", "О плавающих телах". Среди утраченных произведений – сочинение арифметического содержания, сочинение о многогранниках, а также сочинения прикладного характера: о рычагах, об отражении и преломлении световых лучей, об изготовлении шаров. Написаны эти сочинения преимущественно в виде писем, каждое из которых представляет собой оригинальное сочинение. Ни в одном нет и намека на заимствование.

Наибольший вклад Архимеда в математику относится к той области, которую теперь мы называем интегральным исчислением: теоремы о площадях плоских фигур, объёмах тел и центрах тяжести.

Развитие в 4-3 веке до н.э. теории конических сечений, статики и гидростатики потребовало вычисления ряда новых площадей и объёмов и – впервые в истории науки – центров тяжести. Решая подобные задачи, Архимед не только использовал старые формы метода исчерпывания, но ввёл и существенно новые схемы таких доказательств.

Одна из таких схем доказательства, часто использовавшаяся Архимедом, может быть проиллюстрирована выполненной им квадратурой сегмента параболы.

Для определения площади сегмента параболы, изображенной на рисунке 1, Архимед, проведя из середины основания AC прямую DB, параллельную оси параболы, вписывает в него треугольник ABC и доказывает, что площадь рассматриваемого сегмента равна площади треугольника ABC.

Рисунок 1

Для этого в оба параболических сегмента, отсеченных прямыми AB и BC, Архимед вписывает треугольники AEB и BFC, так же, как в первоначальный сегмент был вписан треугольник ABC, и опираясь на свойства параболы, показывает, что взятые вместе эти треугольники будут в четыре раза меньше треугольника ABC.

Последний факт легко установить в случае, когда прямая BD перпендикулярна AC. Действительно, в этом случае , откуда площади каждого из треугольников AEK, BEK, BFL и CFL равны , а их сумма - . В то же время площадь треугольника ABC равна

Если процесс последовательного вписывания всё новых треугольников будет продолжаться, то на втором этапе мы получим 4 треугольника, которые все вместе будут в четыре раза меньше суммы двух предыдущих треугольников, а на третьем – 8 треугольников, которые все вместе в четыре раза меньше четырех предыдущих и т.д.

Если площадь треугольника ABC обозначить C₁, то площадь многоугольника AEBFC будет равна , а площади следующих многоугольников, соответственно , и .

Затем Архимед доказывает, что если к любой из этих сумм прибавить третью часть её последнего члена, то сумма станет равной . Действительно, прибавив, например, к сумме 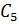третью часть ее последнего члена, то есть , мы получим выражение 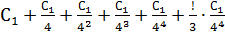. Сложив два последних слагаемых получим , т.е. третью часть последнего члена предыдущей суммы C₄. Повторив эту процедуру еще три раза, Архимед получает, что

В общем случае можно доказать, что

(1)

Процесс последовательного вписывания треугольников может продолжаться неограниченно. При этом, как легко видеть, площадь каждого вписываемого треугольника больше половины сегмента, в который он вписывается, и поэтому разность между площадью рассматриваемого параболического сегмента, которую мы обозначим буквой Z, и площадью вписываемых многоугольников C_n может быть сделана как угодно малой.

Выполнив эту подготовительную работу, Архимед методом от противного доказывает, что .

Для этого рассматриваются два случая: и и показывается, что оба они приводят к противоречию.

Действительно, если предположить, что , то, продолжая процесс увеличения числа сторон вписываемых многоугольников, можно числу n придать такое значение, что

(2)

С другой стороны, из (1) следует, что , откуда

откуда , что противоречит построению вписываемых многоугольников.

Аналогично доказывается невозможность неравенства , откуда следует, что

Рисунок 2

Доказательства по методу исчерпывания заключали в себе идеи позднейшей теории пределов и содержали как важнейший элемент сколь угодно точное приближение к искомой величине – пределу. Заключение от противного, неразрывно связанное с этим неограниченным приближением, гарантировало единственность предела. Однако в методе исчерпывания не были выделены ни идея переменной величины, ни идея предела, ни, тем более, какие-либо общие свойства последнего. В отличие от современной теории

пределов, где теорема о единственности предела доказывается (также от противного) сразу в общем случае, в античном методе это доказательство проводилось в каждой задаче заново.

В других задачах Архимед впервые применил составление настоящих интегральных сумм: "верхней" и "нижней", первая из которых превосходит измеряемую величину, а вторая меньше её. Члены этих сумм неограниченно уменьшаются, число их неограниченно растёт, а разность между ними (и измеряемой величиной) стремится к нулю.

Простейшим примером применения этого метода является выполненное Архимедом кубирование параболоида вращения. Для этого он рассекает данный сегмент параболоида плоскостями, параллельными основанию, на слои одинаковой толщины (рисунок 2) и каждый из этих слоев заключает между двумя цилиндрами, из которых один больше, а другой меньше рассматриваемого слоя.

Пусть симптом параболы, вращением которой получен данный параболоид, имеет вид 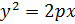, а толщина слоя равна h. Тогда объем первого сверху описанного цилиндра В то же время при переходе от k-го слоя к (k+1) -му слою его объем увеличивается на величину

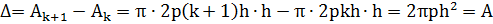
и, следовательно, объемы внешних цилиндров образуют арифметическую прогрессию, разность которой равна наименьшему члену. В результате сумма всех n описанных вокруг параболоида цилиндров равна

.

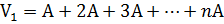Сумма же внутренних цилиндров, образующих такую же прогрессию, но только без последнего члена, равна

.

Воспользовавшись формулой суммы членов арифметической прогрессии, получим, что 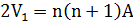, а . Легко видеть, что произведение n 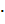nA удовлетворяет неравенству

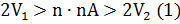
Рассматриваемое произведение n 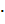nA можно истолковать как объем n цилиндров, каждый из которых равен нижнему описывающему цилиндру или, что всё равно, объему цилиндра, имеющего то же самое основание и ту же высоту, что и сегмент параболоида. Если объем этого цилиндра обозначить буквой V, то вместо (1) можно написать:

или (2)

Далее, если Z есть объем сегмента параболоида, то

(3)

Так как разность V₁-V₂, равная объему самого нижнего цилиндра, может быть сделана сколь угодно малой, то из (2) и (3) методом от противного Архимед получает результат: . Таким образом, он доказал, что объем сегмента параболоида вращения равен половине объема цилиндра, имеющего то же самое основание и ту же высоту.

В случае эллипсоида или гиперболоида цилиндры уже не составляют арифметической прогрессии, и, по собственному признанию Архимеда, ему лишь с большим трудом удалось, пользуясь тем же методом, найти искомые объемы.

Хотя среди различных приёмов Архимеда встречаются настоящие интеграционные методы, однако он не выделил общего содержания интеграционных приёмов и понятия об интеграле, а тем более не создал алгоритма интегрального исчисления. Сам запас вычислительных средств интегрального исчисления оставался весьма ограниченным (суммы геометрической прогрессии, ряд квадратов и немногие другие), а внешняя форма изложения, чисто словесная, сильно затрудняла изучение работ Архимеда. После него, вплоть до конца античной эпохи, существенно новых результатов в интегральном исчислении получено не было. Со второго века до н.э. деятельность учёных в области классических представлений античной математики стала постепенно вырождаться в комментаторство. Подлинное возрождение приёмов Архимеда наступило только в новое время.

Основной особенностью математических сочинений Архимеда является применение строгих математических методов в разработке экспериментально-теоретического материала из области механики и физики. В сочинении "О равновесии плоских фигур" впервые строго логически из целого ряда аксиом выводится знаменитый закон рычага: Две величины уравновешивают друг друга, если их расстояния будут обратно пропорциональны весам. При помощи этого закона определяются центры тяжести параллелограмма, треугольника и трапеции, а во второй книге – центр тяжести параболического сегмента, а также центр тяжести части площади параболы, заключённой между двумя параллельными прямыми.

Такая особенность делает труды Архимеда едва ли не наиболее ярким образцом развития прикладных математических знаний, техники вычислений и новых математических методов, в особенности инфинитезимальных, в эпоху поздней античности.

Рисунок 3

В творчестве Архимеда работы по механике занимали настолько большое место, что механические приёмы и аналогии проникли даже в математические методы. Ко многим своим открытиям Архимед пришёл, сочетая принципы теории рычага с рассмотрением "неделимых" элементов фигур. Результаты, найденные таким путём, Архимед, в соответствии с принятым в ту эпоху стандартом строгости, доказывал методом исчерпывания.

До недавнего времени о таком проникновении нельзя было судить достоверно. Вопрос окончательно прояснился после того, как в 1906 году было найдено сочинение Архимеда "Послание к Эратосфену" о механическом методе решения геометрических задач. Метод проиллюстрируем на примере доказательства того, что объем шара относится к объему описанного около него цилиндра, как 2 относится к 3 – результат, который открывал путь ко многим другим теоремам и который сам Архимед особенно ценил. Цицерон в своих воспоминаниях утверждал, что он видел мраморную плиту на могиле Архимеда с изображением шара, вписанного в цилиндр.

Для предварительного, чернового доказательства высказанного выше утверждения Архимед одновременно с шаром строит конус и цилиндр, радиусы оснований и высоты которых равны диаметру шара. Сочетание этих тел легко представить, мысленно вращая рисунок 27 вокруг оси AB. Затем через все эти тела проводится сечение, параллельное основаниям цилиндра и конуса, на некотором произвольном фиксированном расстоянии BO от них. На чертеже его следом является прямая MN.

Тогда по теореме Пифагора

AK²=OK²+OA²=OK²+OL²,где OK и OL – радиусы кругов, образованных сечением шара и конуса плоскостью MN. С другой стороны, по свойству хорды AK²=AB OA. Подставив полученное значение AK² в предыдущее равенство, получим: AB OA=OK²+OL². Умножив обе части на и сгруппировав, получим равенство:

или, учитывая, что AB=OM,

представляющее собой соотношение между площадями сечений цилиндра, шара и конуса плоскостью MN.

В этой части все рассуждения вполне соответствуют античному пониманию строгости. Иначе обстоит дело со второй частью рассуждений. Здесь Архимед каждое из трех рассматриваемых тел представляет как бы составленным из "элементов" – круговых сечений, перпендикулярных оси AB, что явно противоречило установившимся в то время взглядам и не допускалось в строгих рассуждениях. Затем от точки A в направлении, противоположном AB, он откладывает отрезок AO₁, равный отрезку AB, и весь отрезок BO₁ рассматривает в качестве рычага с опорой в точке A.

После этого Архимед, заменив в формуле (1) AB на AO₁, получает равенство:

которое в соответствии с выведенным им правилом рычага интерпретирует как утверждение о равновесии: элемент цилиндра , закреплённый в точке O, уравновешивает элементы шара 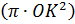и конуса 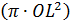, закрепленный в точке O₁. Переходя к объемам тел, “составленных” из таких элементов, Архимед получает равенство:

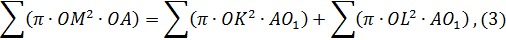
где знак суммы означает "все вместе взятые".

Так как центр тяжести цилиндра находится в точке C, то в соответствии с теорией рычага .

Учитывая это обстоятельство, и то, что AO₁ постоянный отрезок, получим:

Следуя своей гипотезе, Архимед полагает, что 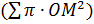- объём цилиндра, – объём шара, а -объём конуса, с учетом чего равенство (4) можно записать в виде:

Учитывая, что AB=2AC, получим: , откуда . Но, как доказывается в “Началах”, ,

откуда .

Перейдем теперь от большого цилиндра к цилиндру, описанному около шара, объем которого обозначим V_оп.цил. Так как радиус основания этого цилиндра в 2 раза меньше радиуса большого цилиндра, то V_цил=4V_оп.цил, откуда V_оп.цил, или как выражал это соотношение Архимед, V_шар:V_оп.цил=2:3.

Такой способ механической аналогии применён Архимедом и в сочинении "О квадратуре параболы".

В соответствии с научной традицией своего времени Архимед результаты, полученные методом механической аналогии, переводил на общепринятый язык метода исчерпывания с обязательным завершением последнего доказательством от противного.

Архимед разрабатывал и методы, близкие к тем, которые теперь называют дифференциальными. Соответствующий пример, связанный с построением касательной к спирали .

В отличие от работ большинства творческих математиков Греции, в произведениях Архимеда много вычислений. Это придаёт его трудам, при всех их типично греческих особенностях, восточный оттенок. Такой отпечаток заметен в его "Задаче о быках" – очень сложной задаче неопределенного анализа, которую можно истолковать как задачу, приводящую к уравнению t²-4729494 u²=1 типа "уравнения Пелля", которое решается в очень больших (целых) числах. Это лишь одно из многих указаний на то, что традиции Платона никогда безраздельно не господствовали в математике эллинизма, на то же самое указывает эллинистическая астрономия.

В "Измерении круга" Архимед нашёл приближённое выражение для окружности, пользуясь вписанными и описанными правильными многоугольниками. Дойдя в этом приближении до многоугольников с 96 сторонами, он нашёл (в наших обозначениях), что

Обычно об этом сообщают, говоря, что примерно равно

Каждое новое сочинение Архимеда прибавляло нечто новое к совокупности знаний, которыми владели его предшественники в арифметике, в геометрии, в механике, в астрономии. Во все отрасли точного знания он сделал вклады, не только сохранившие своё значение до настоящего времени, но часто служащие основой современных дисциплин, теоретических и прикладных. В математическом творчестве Архимеда отчетливо просматривается смещение интереса к фигурам и пространственным телам, ограниченным кривыми линиями и поверхностями, прежде всего, кривыми второго порядка и образуемыми ими поверхностями. Чрезвычайной оригинальностью, глубиною мысли и свежестью замысла отличается каждая из его работ. История науки знает очень мало произведений такого яркого творчества, такой гениальной мысли.

 

Задача Иосифа Флавия.

Формулировка задачи: в круг выстроено n человек, пронумерованных числами от 1 до n, и исключается каждый второй из оставшихся до тех пор, пока не уцелеет только один человек. Определить номер уцелевшего, J(n).

Например, при n = 10 порядок исключения – 2, 4, 6, 8, 10, 3, 7, 1, 9, так что остается номер 5, т.е. J(10) = 5. При n = 2 номер уцелевшего J(2) = 1. Можно было бы предположить, что J(n) = при четном n. Однако это не так – предположение нарушается при n = 4 и n = 6.

 

N
J(n)

 

J(n) всегда будет нечетно, т.к. первый обход по кругу исключает все четные номера. К тому же, если само n четно, мы приходим к ситуации, подобной той, с которой начали, за исключением того, что остается вдвое меньше людей, и их номера меняются.

Итак, решим поставленную задачу.

Допустим, что первоначально имеется 2n людей. После первого обхода мы остаемся с номерами:

….

2n-3

2n-1

Следующий обход будет начинаться с номера 3. Это тоже самое, если бы мы начинали с n людей, за исключением того, что номер каждого уцелевшего удваивается и уменьшается на 1. Тем самым

J(2n) = 2∙J(n) − 1 при n ≥ 1 (5)

Теперь можно быстро продвигаться к большим n. Например, нам известно, что J(10) = 5, поэтому J(20) = 2∙J(10) − 1 = 2∙5 − 1 = 9, аналогично J(40) = 2∙J(20) − 1 = 17, и вообще можно вывести, что

J(5∙2^m) = 2^m+1+1.

J(5∙2^m) = J(2∙2^m-1∙5) = 2∙J(2^m-1∙5) − 1 = 2∙J(2∙2^m-2∙5) − 1 = 2²∙J(2^m-2∙5)− 2¹ − 1 = =2³∙J(2^m-3∙5) − 2² − 2¹ − 1=2⁴∙J(2^m-4∙5) − 2³ − 2² − 2¹ − 1= …= 2^m∙J(5) − (2^m-1+2^m-2+ +…+2³+2²+2¹+1) = 2^m∙J(5) − = 2^m∙3 − 2^m + 1 = 2^m+1+1.

Теперь посмотрим, что будет в случае, когда имеется 2n+1 людей. После первого обхода жертва с номером 1 уничтожается сразу после жертвы с номером 2n, и мы остаемся с номерами:

….

2n-1

2n+1

Получили почти первоначальную ситуацию с n людьми, но на этот раз номера уцелевших удваиваются и увеличиваются на 1. Таким образом,

J(2n+1) = 2∙J(n) + 1 при n ≥ 1 (6)

Объединение уравнений (5) и (6) с уравнением J(1)=1 дает рекуррентное соотношение, которое определяет J во всех случаях:

J(1) = 1

J(2n) = 2∙J(n) − 1 при n ≥ 1 (7)

J(2n+1) = 2∙J(n) + 1 при n ≥ 1

Решим данное рекуррентное соотношение. Составим таблицу первых значений J(n):

n		2 3	4 5 6 7	8 9 10 11 12 13 14 15
J(n)		1 3	1 3 5 7	1 3 5 7 9 11 13 15

 

Если сгруппировать значения n по степеням двойки (в таблице эти группы отделены вертикальными линиями), то в каждой группе J(n) всегда будет начинаться с 1, а затем увеличиваться на 2. Итак, если записать n в виде n = 2^m+k, где 2^m – наибольшая степень 2, не превосходящая n, а k – то, что остается, то решение рекуррентного соотношения должно иметь вид:

J(2^m+k) = 2k+1 при m ≥ 0 и 0 ≤ k < 2^m (8)

(Если 2^m ≤ n < 2^m+1, то остаток k = n−2^m удовлетворяет неравенству 2^m≤k+2^m<2^m+1, т.е. 0 ≤ k < 2^m)

 

 

Докажем (8) методом математической индукции по m.

1) База: m = 0 => k = 0

J(2⁰+0) = J(1) = 2∙0 + 1 = 1 (верно);

2) Индуктивный переход: пусть верно для всех чисел t ≤ (m − 1). Докажем для t=m:

если m > 0 и 2^m+k=2n, то k – четно и J(2^m+k) = J(2(2^m-1+ )) = 2∙J(2^m-1+ ) − 1 2(2∙ + 1) −1 = 2k + 1;

если m > 0 и 2^m+k=2n+1, то k – нечетно (т.е. k=2t+1) и J(2^m+k) = = J(2^m+(2t+1)) = J(2(2^m-1+t) +1) 2∙J(2^m-1+ t) + 1 2(2t+1) + 1 = 2k + 1.

Другой способ доказательства, когда k – нечетно:

Можно заметить, что J(2n+1) − J(2n) = 2, тогда J(2^m+k) = 2 + J(2^m + (k− −1)) 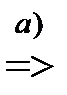J(2^m+k) = 2 + 2(k −1) + 1 => J(2^m+k) = 2k+1.

Из пунктов 1 и 2 следует: при m ≥ 0 и 0 ≤ k < 2^m J(2^m+k) = 2k+1.

Решение всякой задачи может быть обобщено так, что его можно применить к более широкому кругу задач. Поэтому изучим решение (8) и исследуем некоторые обобщения рекуррентного соотношения (7).

Обратимся к двоичным представлениям величин n и J(n) (т.к. степени 2 играли важную роль в нашем поиске решения).

n = (b_m b_m-1 … b₁ b₀)₂;

т.е. n = b_m2^m + b_m-12^m-1 + … + b₁2 + b₀

где каждое b_i равно 0 или 1, причем старший бит b_m равен 1. Вспоминая, что n=2^m+k, последовательно получаем:

n = (1 b_m-1 … b₁ b₀)₂

k = (0 b_m-1 … b₁ b₀)₂

(т.к. k= n−2^m = 2^m + b_m-12^m-1 + … + b₁2 + b₀ − 2^m = 0∙2^m + b_m-12^m-1 + …+ b₁2 + b₀)

2k = (b_m-1 … b₁ b₀ 0)₂

(т.к. 2 k=2(b_m-12^m-1 +b_m-22^m-2 …+ b₁2 + b₀)=b_m-12^m + b_m-22^m-1 + … + b₁2² + b₀2+0)

2k+1 = (b_m-1 … b₁ b₀ 1)₂

J(n) = (b_m-1 … b₁ b₀ b_m)₂

(т.к. J(n) = 2k+1 и b_m = 1)

Таким образом, мы получили, что

J((b_m b_m-1 … b₁ b₀)₂) = (b_m-1 … b₁ b₀ b_m)₂ (9)

т.е. J(n) получается путем циклического сдвига двоичного представления n влево на один сдвиг.

Рассмотрим свойства функции J(n).

Если мы начнем с n и итерируем J-функцию m+1 раз, то тем самым осуществляем циклический сдвиг на m+1 битов, а т.к. n является (m+1)-битовым числом, то мы могли бы рассчитывать в итоге снова получить n. Но это не совсем так. К примеру, если n = 27, то J(11011) = ((10111)₂), но затем J(10111) = ((1111)₂), и процесс обрывается: когда 0 становится старшим битом – он пропадает (т.к. принято, что коэффициент при старшей степени не равен 0). В действительности J(n) всегда должно быть ≤ n по определению, т.к. J(n) есть номер уцелевшего; и если J(n) < n, мы никогда не сможем получить снова n в следующих итерациях.

Многократное применение J порождает последовательность убывающих значений, достигающих, в конце концов «неподвижной точки» n, такой, что J(n)=n. Докажем, что J порождает последовательность убывающих значений, т.е. покажем, что 2ⁿ > 2^n-1 + 2^n-2 +…+2¹ + 1 при n ≥ 1.

Докажем методом математической индукции по n:

1) База: n=1, 2¹ > 2⁰ (верно);

2) Индуктивный переход: пусть верно для всех чисел t ≤ (n–1), т.е. выполняется неравенство 2^t-1 > 2^t-2 + 2^t-3 +…+2¹ + 1. Докажем для t=n:

(2^n-1 > 2^n-2 + 2^n-3 +…+2¹ + 1) умножим на 2, получим 2ⁿ > 2^n-1 + 2^n-2 +…+2² + 2¹. Левая и правая части неравенства четные числа, тогда между ними есть хотя бы одно нечетное число, следовательно, прибавление 1 к правой части неравенства (четное число +1 = нечетное число) неравенство не изменит. Т.о. получаем нужное нам неравенство: 2ⁿ > 2^n-1 + 2^n-2 +…+2¹ + 1 при n ≥ 1.

Свойство циклического сдвига позволяет выяснить, чем будет «неподвижная точка»: итерирование функции m и более раз всегда будет порождать набор из одних единиц со значением 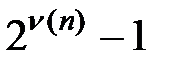, где ν(n) – число равных 1 битов в двоичном представлении n (это следует из того, что имеем последовательность 2⁰ , 2¹ , 2² ,…,2^n-1, 2ⁿ, и по формуле суммы геометрической прогрессии получаем ).

Так, например: ν(27) = ν(11011) = 4, тогда J(J(…J(27)…)) =2⁴ −1=15

2 и более

Теперь давайте вернемся к нашему первоначальному предположению, что J(n) = при четном n. Вообще-то это неверно, но мы выясним, когда это верно: J(n) = , тогда 2k+1 = => k = .

Если число k = = целое, то n= 2^m + k будет решением, т.к. k < 2^m. Нетрудно убедиться, что (2^m − 2) кратно 3, когда m нечетно, но не когда m четно. Действительно, если m – нечетно, то 2^m − 2 = 2^2k+1 − 2 = 2(4^k − 1). Докажем методом математической индукции, что (4^k − 1) делится на три (где ):

1) База: k=1, 4−1=3, три делится на три (верно);

2) Индуктивный переход: пусть верно для всех чисел t ≤(k−1), т.е (4^t−1) делится на три. Докажем для t=k:

4^k − 1 = 4(4^k-1 − 1) + 3 (4^k-1 − 1) делится на три, и 3 делится на три => (4^к−1) делится на три.

Таким образом, показали, что для m – нечетного (2^m − 2) делится на 3.

Теперь покажем, что при m – четном (2^m − 2) не делится на 3. Предположим противное: пусть (2^m − 2) делится на 3 при четном m, тогда , числа 2 и 3 взаимно простые, следовательно,

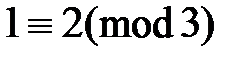() должно делится на 3, т.е. =3q , но , a , т.е. получили, что , а это не верно. Следовательно, наше предположение не верно и 2^m − 2 не делится на 3 при четном m.

Таким образом, имеем бесконечно много решений уравнения J(n) = , и первые такие:

m	k	N= 2m + k	J(n) =2k+1=	n (двоичное)

 

Правый крайний столбец содержит двоичные числа, циклический сдвиг которых на одно позицию влево дает тот же самый результат, что и обычный сдвиг на одну позицию вправо (деление пополам).

Далее обобщим J - функцию, т.е. рассмотрим рекуррентность схожую с (7), но с другими константами: α, β и γ; найдем решение в замкнутой форме.

f(1) = α,

f(2n) = 2f(n) + β при n ≥ 1, (10)

f(2n + 1) = 2f(n) + γ при n ≥ 1.

 

Составим таблицу для малых значений n:

n f(n)   α   2α + β 2α + γ   4α + 3β 4α + 2β + γ 4α + β +2γ 4α +3γ   8α + 7β 8α + 6β + γ

Анализируя таблицу можно сделать предположение, что коэффициенты при α равны наибольшим степеням 2, не превосходящим n; между последовательностями 2 коэффициенты при β уменьшаются на 1 вплоть до 0, а при γ увеличиваются на 1, начиная с 0. Если выразить f(n) в виде:

f(n) = A(n)∙α + B(n)∙β + C(n)∙γ (11)

то, по-видимому,

A(n) = 2^m ,

B(n) = 2^m −1−k, (12)

С(n) = k.

Здесь n = 2^m + k и 0 ≤ k < 2^m при n ≥ 1.

Докажем соотношения (11) и (12).

Докажем (11) методом математической индукции по числу n и при этом будем полагать, что (12) выполняется.

1) База: n=1=2⁰+0 (m=k=0), f(1) =A(1)∙α+B(1)∙β+C(1)∙γ= =2⁰∙α+(2⁰−1−0)∙β+0∙γ = α (верно);

2) Индуктивный переход: пусть верно для всех чисел t ≤ (n–1), т.е. выполняется равенство f(t) = A(t)∙α + B(t)∙β + C(t)∙γ. Докажем для t=n:

a) если n – четное, тогда k тоже четное, т.е. k = 2t, и f(n) = f(2^m+2t) = =f(2(2^m-1 + t)) 2∙f(2^m-1 + t)+β 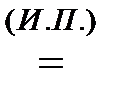2∙(A(2^m-1 + t)∙α + B(2^m-1 + t)∙β + C(2^m-1 + +t)∙γ) + β 2(2^m-1∙α + (2^m-1−1−t)∙β + t∙γ) + β = 2^m∙α + (2^m−1−2t)∙β + 2t∙γ = 2^m∙α+ + (2^m−1−k)∙β + k∙γ = A(n)∙α + B(n)∙β + C(n)∙γ;

b) если n - нечетное, тогда k тоже нечетно, т.е. k=2t+1, и f(n) = =f(2^m+2t+1) = f(2(2^m-1 + t)+1) 2∙f(2^m-1 + t)+ γ 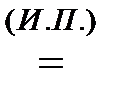2∙(A(2^m-1 + t)∙α + B(2^m-1 + +t)∙β + C(2^m-1 + t)∙γ) + γ 2(2^m-1∙α + (2^m-1−1−t)∙β + t∙γ) + γ = 2^m∙α + +(2^m−1−(2t+1))∙β + (2t+1)∙γ = 2^m∙α+ + (2^m−1−k)∙β + k∙γ = A(n)∙α + B(n)∙β + C(n)∙γ.

Из пунктов 1 и 2 следует: для n ≥ 1 f(n) = A(n)∙α + B(n)∙β + C(n)∙γ.

Теперь докажем (12) в предположении, что (11) выполняется.

Если n - четное, тогда по соотношению (10) f(2n) = 2f(n) + β. Подставляя в данное равенство соотношение (11) получим:

A(2n)∙α + B(2n)∙β + C(2n)∙γ = 2(A(n)∙α + B(n)∙β + C(n)∙γ) + β

(A(2n) − 2A(n))∙α + (B(2n) − 2B(n)−1)∙β + (C(2n) − 2C(n))∙γ = 0

Теперь подставим соотношение (12) в данное равенство и посмотрим, будет ли оно выполнятся: т.к. n = 2^m + k => 2n = 2^m+1+2k, тогда A(2n) = 2^m+1 , B(2n)=2^m+1−1−2k, С(n)=2k. Подставляем: (2^m+1 −2∙2^m)∙α + +(2^m+1−1−2k−2(2^m−1−k)−1)∙β + (2k −2k)∙γ = 0 0∙α + 0∙β + 0∙γ = 0, получили 0=0 (верно);

Если n - нечетное, тогда по соотношению (10) f(2n+1) = 2f(n) + γ. Снова подставляя в данное равенство соотношение (11) получим:

A(2n+1)∙α + B(2n+1)∙β + C(2n+1)∙γ = 2(A(n)∙α + B(n)∙β + C(n)∙γ) + γ

(A(2n+1) − 2A(n))∙α + (B(2n+1) − 2B(n))∙β + (C(2n+1) − 2C(n)−1)∙γ = 0

Теперь подставим соотношение (12) в данное равенство и посмотрим, будет ли оно выполнятся: n = 2^m + k => 2n+1 = 2^m+1+2k+1, тогда A(2n+1) = 2^m+1 , B(2n+1) = 2^m+1 −1−(2k+1), С(n+1) = 2k+1. Подставляем: (2^m+1 −2∙2^m)∙α + +(2^m+1−2−2k−2(2^m−1−k))∙β + (2k+1 −2k−1)∙γ=0 0∙α + 0∙β + 0∙γ = 0, получили 0=0 (верно).

Таким образом, мы показали, что соотношения (11) и (12) верные.

Выше было показано, что J – рекуррентность имеет решение в двоичной записи: J((b_m b_m-1 … b₁ b₀)₂) = (b_m-1 … b₁ b₀ b_m)₂, где b_m = 1. Можно показать, что и обобщенная рекуррентность (10) имеет похожее решение.

Запишем соотношение (10) следующим образом:

(15)

f(1) = α,

f(2n + j) = 2f(n) + β_j при j = 0, 1 и n ≥ 1,

если положить β₀ = β и β₁ = γ. Тогда:

f((b_m b_m-1 … b₁ b₀)₂) = 2f((b_m b_m-1 … b₁)₂) + β_b = 4f((b_mb_m-1…