ИНСТИТУТ ПАРЛАМЕНТАРИЗМА И ПРЕДПРИНИМАТЕЛЬСТВА
Г.М. БУЛДЫК
ЭКОНОМИКО – МАТЕМАТИЧЕСКИЕ МЕТОДЫ
И
МОДЕЛИ
Часть I
Минск, 2010
УДК 338.2(075.8)
ББК 65.050я73
Б90
Р е ц е н з е н т ы: доктор физико-математических наук, профессор В.В. Амелькин;
кандидат физико-математических наук, доцент А.Е. Руденок
Рекомендовано к изданию Научно-методическим советом института, протокол № 2 от “ “ ноября 2010 года.
Булдык Г.М.
Б90 Экономико-математические методы и модели.Учебное пособие в 2 ч. Часть I. – Мн.: ИПП. – 108 с., [ил.].
Рассматриваются современные методы математического моделирования различных экономических процессов.
Для студентов экономических специальностей вузов; полезно экономистам-практикам.
Булдык Георгий Митрофанович – доктор педагогических наук, профессор по специальности «Математика». Автор более134 научно-методических работ. Среди них учебник «Статистическое моделирование и прогнозирование», учебные пособия: «Теория вероятностей и математическая статистика», «Сборник задач и упражнений по высшей математике. Теория вероятностей и математическая статистика», «Руководство к решению задач и упражнений по теории вероятностей и математической статистике», «Сборник задач и упражнений по высшей математике».
Основные научные интересы связаны с разработкой современной концепции преподавания математики. Г.М. Булдык является автором монографий: «Формирование математической культуры студентов экономических специальностей», «Многофакторные динамические модели».
© Булдык Г.М., 2010
ПРЕДИСЛОВИЕ
Моделирование экономических процессов в последнее время является наиболее быстро развивающимся направлением экономической науки и ее важнейших приложений.
Преимущества математики как средства научного познания раскрываются при построении математических моделей, заменяющих в определенных отношениях исследуемые объекты. Математические модели экономики, отражающие с помощью математических соотношений основные свойства экономических процессов и явлений, представляют собой эффективный инструмент исследования сложных экономических проблем.
В данном учебном пособии основное внимание уделяется приложениям математических методов к исследованию реальных экономических процессов. Показано, что математическое моделирование существенно расширяет возможности экономического анализа, повышает качество принимаемых экономических решений.
Главными задачами курса являются: 1) расширение и углубление теоретических знаний о количественных взаимосвязях и закономерностях экономического развития, механизмах управления народным хозяйством; 2) овладение методологией и методикой построения, анализа и применения математических моделей экономических процессов; 3) изучение наиболее характерных моделей и получение навыков практической работы с моделями, используемыми в практике.
Изучение экономико – математических методов и моделей требует математической подготовки по линейной алгебре, дифференциальному исчислению, дифференциальным уравнениям, теории вероятностей и математической статистике. Математические доказательства утверждений часто опускаются, поскольку основное внимание в учебном пособии уделяется приложениям математического аппарата.
Введение
Экономико-математическое моделирование как средство для принятия
Эффективных решений
Предметом изучения дисциплины экономико-математические методы и модели являются количественные характеристики экономических процессов, протекающих в промышленном производстве, и их взаимосвязи. В курсе рассматриваются экономические задачи и их математические модели.
Под математической моделью понимается система математических соотношений (уравнений: алгебраических, дифференциальных, интегральных, в частных производных; графов; соотношений математической логики и др.) описывающих реальный объект, составляющие его характеристики и взаимосвязи между ними.
Таким образом, любая экономико-математическая модель выражает в математических соотношениях экономическую сущность условий задачи и поставленной цели исследования, т. е. экономические связи между экономическими параметрами или величинами описываются математическими соотношениями. Академик Немчинов писал: «Экономико-математическая модель представляет собой концентрированное выражение общих взаимосвязей и закономерностей экономического процесса в математической форме».
Классификация экономико-математических моделей условна и зависит от того, с использованием каких признаков строится модель. Так, например, экономико-математические модели можно подразделить на: статистические, балансовые и оптимизационные.
Статистические – это модели, в которых описываются корреляционно-регрессионные зависимости результата производства от одного или нескольких независимых факторов. Эти модели широко используются для построения производственных функций, а также при анализе экономических систем.
Балансовые модели представляют систему балансов производства и распределения продукции и записываются в форме квадратных матриц. Балансовые модели служат для установления пропорций и взаимосвязей при планировании различных отраслей народного хозяйства.
Оптимизационные модели представляют систему математических уравнений, линейных или нелинейных, подчиненных определенной целевой функции и служащих для отыскания оптимальных (наилучших) решений экономической задачи. Эти модели описывают условия функционирования экономических систем.
Оптимизационные и балансовые экономико-математические модели содержат систему ограничений и целевую функцию.
Система ограничений состоит из отдельных математических уравнений или неравенств, называемых балансовыми уравнениями или неравенствами. Целевая функция связывает между собой различные величины моделей. Это функция многих переменных. В качестве цели, как правило, выбирается экономический показатель: прибыль, рентабельность, себестоимость, объем валовой продукции и т. д.
Критерий оптимальности – это также экономический показатель, выражающийся при помощи целевой функции через другие экономические показатели. Одному и тому же критерию оптимальности могут соответствовать несколько разных, но эквивалентных целевых функций. Критерии оптимальности могут быть натуральные и стоимостные. Одни из критериев – максимизирующие (например, максимизировать прибыль предприятия, рентабельность), другие – минимизирующие (например, минимизировать затраты труда при производстве продукции).
Решением экономико-математической модели или допустимым планом называется набор значений неизвестных, удовлетворяющих системе ограничений. Модель имеет бесконечное множество решений (или допустимых планов) и среди них нужно найти единственное, удовлетворяющее системе ограничений и целевой функции.
Допустимый план, удовлетворяющий целевой функции, называется оптимальным. Он, как правило, единственный.
Отметим, что если модель имеет множество оптимальных планов, то для каждого из них значение целевой функции одно и тоже.
Таким образом, для нахождения наилучшего оптимального экономического решения любой экономической задачи, необходимо построить ее математическую модель, структура, которой содержит систему ограничений, целевую функцию, критерий оптимальности и, решить ее методами математической обработки данных.
Для построения математической модели в первую очередь определяется система переменных величин: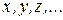 
Переменные могут иметь один индекс 
или несколько индексов 
По каждой переменной для конкретной модели дается пояснение. Затем вводится целевая функция – цель задачи – обозначаемая 
, 
Постоянные величины обозначаются - 
Они также могут иметь индексы: один - 
, или несколько индексов: 
.
Далее составляются основные (все учесть невозможно) ограничения, которые отражают все условия, формирующие оптимальный план.
В построенной, таким образом, экономико-математической модели воспроизводятся лишь основные, наиболее важные в данном исследовании, стороны изучаемого объекта. Поэтому моделирование позволяет выявить существенные факторы, ответственные за те или иные свойства изучаемых явлений.
Следует отметить, что большинство экономико-математических моделей сводится к задачам линейного или нелинейного программирования, и такие модели могут быть представлены в общей, симметричной или канонической форме записи.
Оптимизационные модели
1.1. Общая формулировка оптимизационной модели. Оптимизационные модели представляют систему математических уравнений, линейных или нелинейных, подчиненных определенной целевой функции и служащих для отыскания наилучших (оптимальных) решений конкретной экономической задачи. Эти модели относятся к классу экстремальных задач и описывают условия функционирования экономической системы.
Оптимизационные модели могут носить детерминированный или стохастический характер. В детерминированных моделях результат решения однозначно зависит от входных данных. Стохастические модели описывают случайные процессы, в которых результат всегда остается неопределенным.
Наиболее разработаны и практически более применимы детерминированные модели, использующие аппарат математического программирования.
Структура оптимизационной модели состоит из целевой функции, принимающей значения в пределах ограниченной условиями задачи области, и из ограничений, характеризующих эти условия.
В общем виде оптимизационную математическую модель можно представить в следующем виде:
Найти план 
, который max (min) целевую функцию
(1.1)
при выполнении ограничений
(1.2)
где 
и 
- известные функции, 
- заданные постоянные величины.
Вид целевой функции , вид ограничений и специальные ограничения на переменные (например, требования целочисленности переменных) определяют выбор метода математического программирования для решения оптимизационной задачи:
· линейного программирования;
· нелинейного программирования;
· динамического программирования;
· целочисленного программирования и т. д.
Мы остановимся на оптимизационных моделях, которые решаются методами линейного программирования, т. е. рассмотрим оптимизационные модели (1.1) - (1.2) у которых целевая функция и ограничения - линейные функции. Тогда оптимизационная математическая модель примет вид:
Найти план , который max (min) целевую функцию
(1.3)
при выполнении системы ограничений
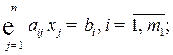(1.4)
(1.5)
(1.6)
(1.7)
Множество планов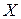 
, удовлетворяющих системе ограничений (1.4) – (1.7), называется множеством допустимых решений и обозначается 
. Допустимый план 
, доставляющий целевой функции (1.3) экстремальное значение, называется оптимальным.
Отметим, что максимизация целевой функции 
в области допустимых решений эквивалентна задаче минимизации функции «
» в той же области: 
.
Если все ограничения задачи заданы в виде равенств и на все переменные 
, наложено условие неотрицательности 
, то оптимизационная модель имеет каноническую форму записи:
max
при ограничениях
.
Если ограничения заданы в виде неравенств, то оптимизационная модель имеет симметрическую форму записи:
max
при ограничениях
,
или
min
при ограничениях
.
Для аналитического решения линейной оптимизационной модели, в случае необходимости, ее ограничения следует преобразовать к каноническому виду, для чего переходят от ограничений неравенств к равенствам, введением дополнительных переменных 
, которые прибавляют к левым частям ограничений неравенств. В целевую функцию дополнительные переменные вводятся с коэффициентами равными нулю.
Примеры линейных оптимизационных моделей
Пример 1. Линейная оптимизационная модель годовой производственной программы предприятия.
Производственная мощность предприятия характеризуется величиной годового максимально – возможного выпуска продукции при применении прогрессивных технологий, эффективной организации производства и наиболее полном использовании производственного оборудования предприятия. Математическая модель для определения производственной программы должна иметь критерий эффективности со стоимостными показателями продукции, хотя они имеют ряд недостатков (изменение цен на продукцию из-за инфляционных процессов, ставок оплаты труда, цен на сырье и др.)
Для построения модели введем обозначения:
· 
- объем производства продукции 
- го вида,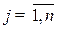 
;
· 
- стоимость единицы продукции - го вида, ;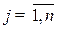
· 
- время обработки - ой продукции на 
- том оборудовании;
· - фонд времени работы оборудования - го вида.
Математическая модель рассматриваемой задачи будет иметь вид:
Найти план выпуска продукции, при котором предприятие получит максимум выручки
при ограничениях на фонд времени работы оборудования
.
Частным случаем рассматриваемой модели является оптимизационная модель использования ресурсов.
Предположим, что предприятие может изготавливать четыре вида продукции 
. Предприятие располагает ресурсами и нормами их расхода, приведенными в таблице 1.1
Таблица 1.1
| Ресурсы | Продукция | Объем ресурса | |||
| П-1 | П-2 | П-3 | П-4 | ||
| Трудовые ресурсы, человеко-смены | 2,5 | 2,5 | 1,5 | ||
| Полуфабрикаты, кг | |||||
| Станочное оборудование, станко-смены | |||||
| Прибыль от единицы продукции, ден. ед. |
Требуется: 1) определить план выпуска продукции, максимизирующей прибыль предприятия;
2) учесть требование комплектации, чтобы количество единиц третьей продукции было в два раза больше количества единиц первой;
3) определить оптимальный ассортимент при дополнительных условиях: первой продукции выпускать не менее 27 единиц, третьей – не более 35, а второй и четвертой – в отношении 2:3.
Построим математическую модель задачи. Для этого введем неизвестные величины 
, характеризующие количество произведенной продукции. Критерий оптимальности – стоимостной (максимум прибыли предприятия). Следовательно, нужно определить план выпуска продукции 
, при котором целевая функция 
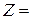
достигает максимального значения и который удовлетворяет системе ограничений:
· на трудовые ресурсы: 
· на полуфабрикаты: 
· на станочное оборудование: 
· условию неотрицательности переменных: 
· дополнительное требование комплектации: 
;
· дополнительные условия: 
Линейная оптимизационная модель построена. Способы решения рассмотрим ниже.
Пример 2. Линейная оптимизационная модель о выборе технологий.
Предположим, что для выпуска некоторой однородной продукции можно использовать 
технологий и при этом используются 
видов ресурсов, заданных соответственно объемами 
Построим математическую модель, решая которую определим оптимальную технологию для выпуска однородной продукции. Пусть: 
- время, в течение которого предприятие выпускает продукцию по - тому технологическому способу;
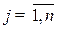, , - стоимость конечной продукции, производимой в единицу времени, по - тому технологическому способу;
- расход - го ресурса в единицу времени по - тому технологическому способу.
Пренебрегая временем переналадок, необходимым для перехода от одного технологического способа к другому, и воспользовавшись стоимостным критерием оптимальности, получим следующую математическую модель рассматриваемой задачи.
Определить оптимальное применение технологических способов 
, при которых максимизируется объем выпуска (в ден. ед.) продукции: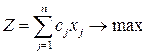 
и, которые удовлетворяют системе ограничений:
Предположим, что предприятие может работать по трем технологическим способам. Расход ресурсов за единицу времени при соответствующей технологии и производительность по каждому технологическому способу (в ден. ед.) в единицу времени, представим в таблице 1.2.
Таблица 1.2
| Ресурсы | Технологические способы | Объем ресурса | ||
| Т-1 | Т-2 | Т-3 | ||
| Трудовые ресурсы, человеко - часов | 1 300 | |||
| Сырье, т | ||||
| Электроэнергия, кВт/ч | 3 000 | |||
| Производительность технологического способа |
Определить план использования технологических способов, при котором максимизируется объем выпуска продукции.
Построим математическую модель задачи. Пусть - время использования - го технологического способа. Требуется найти план , при котором целевая функция
достигает максимального значения, и, который удовлетворяет ограничениям:
Пример 3.Линейная оптимизационная модель раскроя материалов.
На деревообрабатывающем предприятии листы фанеры для изготовления деталей изделий могут раскраиваться несколькими способами. Если лист раскроить по j -му способу раскроя (
), то получится деталей i -го вида (
), при этом отходы с одного листа равны м2. Требуется найти, сколько листов фанеры раскраивать по каждому из способов раскроя, чтобы получить деталей i -го вида не менее единиц, а количество отходов должно быть минимальным.
Составим математическую модель данной задачи.
Обозначим количество листов фанеры, раскраиваемых по j - тому способу. Определим план раскроя листов фанеры так, чтобы суммарное количество отходов по всем вариантам раскроя было минимальным:
и чтобы выполнялись ограничения на изготовление деталей:
Количество листов фанеры, раскраиваемых по j - тому способу, должно быть неотрицательным:
.
Пример 4. Линейная оптимизационная модель о рационе.
Сельскохозяйственное предприятие для откорма скота располагает n видами кормов (сочные, грубые, концентрированные и др.). Каждый вид корма характеризуется содержанием питательных веществ (кормовые единицы, белки, фосфор, кальций и др.). Известно содержание i -го питательного вещества в единице корма j -го вида и равно оно единиц (, ), а также – стоимость единицы корма j -го вида () и минимальная суточная потребность скота в i -м питательном веществе (). Требуется составить рацион минимальной стоимости.
Для построения математической модели данной задачи обозначим - количество корма - го вида. Определим рацион , при котором суммарная стоимость рациона:
будет минимальной, а суточная потребность животного в питательном веществе - го вида будет не менее минимального количества :
Количество корма, потребляемого животным, не может быть отрицательной величиной:
.
Пример 5. Линейная оптимизационная модель о назначениях.
Имеется n механизмов, которые могут использоваться для выполнения n работ. Известна производительность 
каждого i -го механизма (
). Требуется так закрепить механизмы за работами, чтобы суммарная их производительность была максимальной.
Для составления математической модели задачи введем переменные:
Найдем план использования механизмов так, чтобы их суммарная производительность была максимальной:
,
при ограничениях:
· - ый механизм должен быть назначен только на одну работу:
,
· каждая работа должна выполняться только одним механизмом:
.
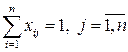Пример 6. Линейная оптимизационная модель о размещениях.
Отраслью заключены договоры на поставку продукции потребителям в заданных ассортименте, объеме и сроках. Для выполнения договорных обязательств руководство отрасли разрабатывает мероприятия по расширению производства на ряде предприятий, проведению их реконструкции, а также строительству и вводу новых мощностей. Требуется определить объемы производства продукции на действующих, реконструируемых и вновь вводимых предприятиях, а также объемы поставок продукции от предприятий-поставщиков к потребителям, чтобы суммарные затраты на производство и доставку продукции были минимальными.
Введем обозначения и построим математическую модель задачи:
i – вид производимой продукции ();
j – номер предприятия, производящего продукцию ();
k – номер потребителя продукции (
);
– мощности j -го предприятия по производству продукции i -го вида;
– стоимость производства единицы продукции i -го вида на j -м предприятии;
– затраты на перевозку единицы продукции i -го вида от j -го предприятия k -му потребителю;
– объем поставки продукции i -го вида k -му потребителю согласно договорным обязательствам;
– искомый объем производства продукции i -го вида на k -м предприятии;
– объем поставки j -м предприятием продукции i -го вида k -му потребителю.
С учетом обозначений суммарные производственные и транспортные затраты в математической модели определяются следующим выражением
.
Ограничения задачи:
· по мощностям каждого предприятия
· по балансу производства и потребления продукции
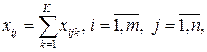
· по удовлетворению спроса потребителей
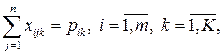
· объемы поставок и производства продукции должны быть неотрицательными:
1.3. Графический способ решения линейных оптимизационных моделей. Рассмотрим линейнуюоптимизационную модель в общей форме записи:
(1.8)
(1.9)
(1.10)
(1.11)
, 
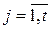; (1.12)
– произвольные, 
.
с геометрической точки зрения. Целевая функция (1.8) определяет семейство параллельных гиперплоскостей уровня цели, каждой из которых соответствует определенное значение функции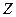 
, так как при изменении 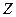коэффициенты не меняются. Поскольку частные производные целевой функции по переменным : 
определяют координаты вектора 
, то вектор 
- это вектор градиентного направления и, следовательно, определяет направление наискорейшего возрастания целевой функции , а вектор 
определяет направление наискорейшего убывания. Неравенства (1.9), (1.11) определяют полупространства, а (1.10) – гиперплоскости. Полупространства и гиперплоскости являются выпуклыми множествами. Множество точек выпукло, если отрезок, соединяющий две произвольные точки этого множества, принадлежит множеству. Пересечение конечного числа выпуклых множеств – множество выпукло. Следовательно, пересечение полупространств и гиперплоскостей определяет выпуклое множество, называемое многогранным множеством или многогранником. Многогранник (ограниченный или неограниченный) – это область допустимых решений линейной оптимизационной модели. Особое значение имеют угловые (или крайние) точки области допустимых решений. Угловой (крайней) точкой выпуклого множества называется точка, если она не является внутренней ни для какого отрезка целиком принадлежащего множеству.
Так как планы линейнойоптимизационной модели – это упорядоченные совокупности n чисел (
), то их можно рассматривать как точки n ‑мерного пространства. Они образуют выпуклое множество, т. е. справедлива теорема:
Теорема. Множество планов линейнойоптимизационной модели является выпуклым.
Доказательство (для канонической линейнойоптимизационной модели). Линейнуюоптимизационную модель можно записать и в матричном виде:
где 
.
Пусть 
и 
– планы канонической линейнойоптимизационной модели. Следовательно, они удовлетворяют системе ограничений: 
и 
. Покажем, что линейная выпуклая комбинация планов и
также является планом данной задачи. Действительно, подставив 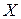в систему ограничений, последовательно преобразовывая, получим верное равенство:
что и требовалось доказать.
Введением дополнительного неравенства:
(достаточно большое)
задачу с неограниченной областью планов формально можно преобразовать в задачу с ограниченной областью.
Поэтому в дальнейшем будем предполагать, что множество планов линейнойоптимизационной модели является выпуклым многогранником и называть его многогранником планов.
Таким образом, линейнуюоптимизационную модель на геометрическом языке можно сформулировать следующим образом: найти точку 
многогранника планов, определяемого системой ограничений (2.2) – (2.5), через которую проходит гиперплоскость семейства (2.1), соответствующая наибольшему (наименьшему) значению функции .
Пусть 
, тогда линейнаяоптимизационная модель на геометрическом языке формулируется следующим образом: найти точку 
многоугольника (многоугольной области) планов, определяемого системой ограничений:
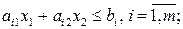(1.13)
,
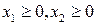через которую проходит прямая семейства
, (1.14)
соответствующая наибольшему (наименьшему) значению функции .
Прямые 
называются линиями уровня. Используя данную геометрическую интерпретацию, линейнуюоптимизационную модель (1.13)- (1.14) можно решить графически. Для этого:
1) нужно построить многоугольник (многоугольную область) планов, т. е. множество допустимых решений Ω с учетом системы ограничений (1.13);
2) построить вектор 
и одну из прямых семейства , например 
;
3) параллельным перемещением прямой в направлении вектора 
найти точку, в которой достигает максимума (минимума);
4) решая совместно уравнения прямых, пересекающихся в точке оптимума, найти ее координаты, а затем 
.
При определении оптимального плана возможны случаи:
1) функция может достигать минимума в одной точке, а максимума – в любой точке отрезка;
2) максимум может достигаться в одной точке, минимума не имеет ( → – 
) или минимум может достигаться в любой точке отрезка;
3) функция не имеет ни максимума ( → + ), ни минимума ( → – ).
Таким образом, оптимальный план может быть единственным; оптимальных планов может быть бесконечное множество; целевая функция может быть не ограничена; задача не имеет решения (см. рис. 1.1).
Рис. 1.1.
Анализируя рассмотренные случаи, можно сделать вывод: если