Каждой линейной оптимизационной модели можно поставить в соответствие другую линейную оптимизационную модель, называемую двойственной по отношению к первой. Так если в первой требуется найти максимум целевой функции 
, то в двойственной модели нужно найти минимум целевой функции F. Целевая функция 
и система ограничений двойственной модели полностью определяются условием исходной модели. Исходная и двойственная модели образуют пару взаимно двойственных моделей.
Рассмотрим линейную оптимизационную модель в канонической форме записи: найти план 
, при котором целевая функция
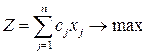, (4.1)
и который удовлетворяет ограничениям:
, (4.2)
.
Двойственная модель формулируется следующим образом: найти план 
, при котором целевая функция
, (4.3)
и который удовлетворяет ограничениям:
. (4.4)
В двойственной модели y 
могут принимать и отрицательные значения, нужно только, чтобы они удовлетворяли системе ограничений (4.4).
Пусть линейная оптимизационная модель записана в симметрической форме: требуется найти план , при котором целевая функция
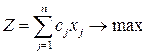, (4.5)
и который удовлетворяет ограничениям:
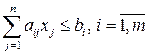, (4.6)
.
Двойственная задача формулируется следующим образом: найти план , при котором целевая функция
, (4.7)
и который удовлетворяет ограничениям:
, (4.8)
.
В рассмотренных парах двойственных моделей каждая из моделей может быть принята за исходную, тогда вторая будет двойственной.
Установим связи между двойственными моделями:
1) упорядочим запись исходной модели: в задаче на максимум ограничения-неравенства должны иметь смысл ≤, в задаче на минимум − ≥.
2) если в прямой модели определяется максимум целевой функции, то в двойственной – минимум, и наоборот;
3) свободные члены ограничений прямой модели служат коэффициентами целевой функции двойственной модели, а коэффициенты целевой функции прямой модели служат свободными членами ограничений двойственной модели;
4) матрицей коэффициентов ограничений двойственной модели служит матрица, полученная транспонированием матрицы коэффициентов ограничений исходной модели;
5) каждому ограничению-неравенству прямой модели соответствует неотрицательная переменная двойственной модели, а каждому ограничению-равенству – переменная произвольного знака.
6) каждой неотрицательной переменной прямой модели соответствует ограничение-неравенство двойственной, а каждой произвольной переменной – ограничение-равенство.
Пример 4.1. Пусть предприятие выпускает n видов продукции и использует при этом m различных видов ресурсов, объем которых ограничен величинами 
, 
,…, 
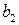. Пусть известны нормы расхода i -го ресурса при производстве единицы j -го вида продукции – 
. Известна также выручка от реализации единицы j -го вида продукции – 
. Требуется найти план 
, при котором выручка была бы максимальной.
Тогда двойственная задача формулируется следующим образом:
Пусть предприятие решило реализовать имеющиеся ресурсы, не выпуская готовую продукцию. При этом оно заинтересовано получить выручку не меньшую чем при изготовлении готовой продукции. Предприятие, которое закупает ресурсы, стремится к тому, чтобы общая стоимость ресурсов была минимальной. Поэтому необходимо установить оптимальные цены на ресурсы 
, …, 
, которые бы удовлетворяли указанным условиям.
4.2. Соответствие между переменными
пары взаимно двойственных линейных оптимизационных моделей. Рассмотрим исходную линейную оптимизационную модель, которая приведена к канонической форме записи введением дополнительных неотрицательных переменных: 
.
Найти максимум целевой функции:
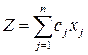(4.9)
при ограничениях:
, (4.10)
; 
; (4.11)
Двойственную модель также приведем к канонической форме записи введением дополнительных неотрицательных переменных 
, …, 
, учитывая, что 
: найти минимум целевой функции
, (4.12)
при ограничениях:
, 
, (4.13)
, 
.
Число переменных в системах (4.10) и (4.13) одинаково и равно n + m.
Базисными переменными в исходной модели будут 
, а в двойственной – переменные 
.
Между базисными переменными исходной и свободными переменными двойственной моделей можно установить следующее соответствие:
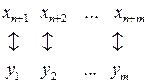
Аналогично устанавливается соответствие между базисными переменными двойственной модели и свободными переменными исходной модели:
Представим модели в виде симплексных таблиц. Таблица для исходной модели имеет вид:
Таблица 4.1
| БП | 
| СП |
 … 
| ||
 =
|
|  … 
|
| … | … | ... |
 =
|
|  … 
|
|
|  … 
|
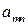
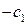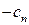
Таблица для двойственной модели:
Таблица 4.2
| Б.П. | А 
| СП |
y  … y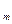 
| ||
| =
|
| …
|
| … | … | ... |
| =
|
| …
|
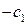
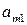
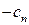
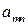
| F | …
|
Положив свободные переменные 
, найдем значения базисных переменных 
, …, 
(табл. 4.1). Если положить переменные 
то получим 
, …, 
(табл. 4.2). Учитывая соответствие между переменными, при решении одной из двойственных моделей, получаем решение другой. Получить решение двойственной модели можно из последней симплексной таблицы прямой модели. Если прямая модель решается на максимум, то оптимальное решение двойственной модели соответствует оценкам индексной строки в последней симплексной таблице прямой модели: 
.
Если прямая модель решается на минимум, то оптимальное решение двойственной модели равно компонентам индексной строки в последней симплексной таблице, взятыми с противоположными знаками, т.е.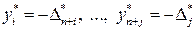 
.
Пример 4.2. На предприятии имеется 4 вида сырья в количествах 
= 18, 
= 16, 
= 8, 
= 6 единиц, из которых выпускаются 3 продукта П , П 
, П 
. Нормы затрат и прибыли от реализации каждого вида продукции приведены в таблице 4.3.
Таблица 4.3
| Сырье | Продукты | Объем сырья | ||
| П
| П
| П
| ||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
| Прибыль | max |
Составить план производства трех видов продукции, при котором доход был бы максимальным. Найти двойственные оценки.
Решение. Пусть 
– количество 
-го вида продукции, = 1, 2, 3. Математическая модель задачи имеет вид: требуется найти план производства продукции 
, при котором функция прибыли 
и который удовлетворяет системе ограничений по запасам сырья: 
Сформулируем двойственную модель. Пусть 
, – оценки единицы сырья 
. Определим оценки сырья 
, при которых функция стоимости сырья 
и которые удовлетворяют системе ограничений:
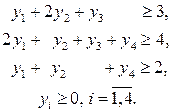
Исходную задачу решим симплекс-методом. Для этого приводим систему ограничений к предпочтительному виду, вводя дополнительные неотрицательные переменные 
. Система ограничений примет вид:
В целевую функцию дополнительные переменные вводятся с коэффициентами равными нулю 
= 0, i = 
: = 
= 
= 
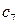= 0.
Составляем симплексную таблицу № 1 (табл.4.4):
Таблица 4.4
| БП |
| СП | |||
- 
| - 
| - 
| |||
| |||||
| |||||
| |||||
| 
| ||||
| -строка
| –3 | –4 | –2 |
Строка функции цели заполняется компонентами, вычисляемыми по формулам: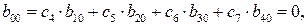 
Наименьшей компонентой индексной строки является «–4». Поэтому разрешающим столбцом является третий столбец. Находим симплексные отношения: 18/2 = 9, 16/1 = 16, 8/1 = 8, 6/1 = 6. Среди них наименьшее равно 6. Следовательно, разрешающей строкой является четвертая строка.
Составляем новую симплексную таблицу № 2 (табл. 4. 5).
Таблица 4.5
| БП |
| СП | |||
| -
| -
| -
| |||
|
| –2 | –1 | |||
|
| –1 | ||||
|
|
| –1 | –1 | ||
|
| |||||
|
| –3 |
Опорный план задачи, после первого шага не является оптимальным, так как в индексной строке есть отрицательный элемент. Соответствующий столбец будет разрешающим.
Находим симплексные отношения: 6/1 = 6, 10/2 = 5, 2/1 = 2. Наименьшее – «2», поэтому разрешающей строкой будет третья строка.
Составляем новую симплексную таблицу № 3 (табл. 4.6):
Таблица 4.6
| БП | 
| СП | |||
- 
| - 
| - 
| |||
| –1 | –1 | |||
| –2 | │2│ | |||
| –1 | –1 | |||
| |||||
|
| –1 |
Так как в Z - строке есть отрицательный элемент, то применяем еще раз симплекс-метод. Составляем симплексные отношения: 6/1 = 6, 6/2 = 3. Выбираем в качестве разрешающей - вторую строку.
Составляем симплексную таблицу № 4 (табл. 4.7):
Таблица 4.7
| БП |
| СП | |||
| -
| -
| -
| |||
|
| –1 | –1 | |||
|
| –1 | 1/2 | 1/2 | ||
|
| –1/2 | 1/2 | |||
|
| 1/2 | –1/2 | |||
|
| 3/2 | 1/2 |
Все элементы индексной строки положительные. Следовательно, построенный опорный план оптимальный. Приравняв свободные переменные нулю,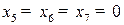 
, получим: 
= (5, 3, 3, 4, 0, 0, 0) и
= 33.
Значение двойственных оценок определим с учетом соответствия между переменными. При построении взаимно двойственных моделей соответствие между переменными следующее:
После решения и введения новых переменных в базис, получим:
Из последней симплексной таблицы находим значения двойственных оценок при условии, что свободные переменные равны нулю, т. е. 
: 
= 
, 
= 2, 
= 
. Оптимальный план будет иметь вид:
= (0, , 2, , 0, 0, 0)
Оценка для сырья 
равна нулю, так как сырье используется не полностью. Для сырья 
, 
, 
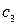оценки положительны, что указывает на полное использование сырья. Значение целевой функции:
= 18 · 0 + 16 · + 8 · 2 + 6 · = 33.
Система ограничений двойственной задачи при подстановке оптимальных значений выполняется:
0 + 2 · + 2 = 3; 2 · 0 + + 2 + 
= 4; 0 + + = 2.
Пример 4.3. Прутки стального проката длиной 600 см, согласно заявкам потребителей, нужно раскраивать на заготовки трех видов с длиной соответственно 
см, 
см и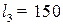 
см для производства 45 изделий. На каждое изделие требуется по 3 заготовки длиной 
, 4 заготовки длиной 
и 5 заготовок длиной 
. Определить, какое количество прутков нужно разрезать для изготовления 45 изделий, чтобы отходы были минимальными.
Решение. Прежде всего, построим таблицу 4.8 возможных вариантов раскроя.
Таблица 4.8
| Способ раскроя | Количество заготовок | Остаток | ||
| =250
| =200
| =150
| ||
| I II III IV V VI |
Обозначим через 
, количество прутков, раскраиваемых - тым способом. Для изготовления 45 изделий необходимо 
заготовок , 
заготовок , 
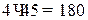заготовок . Если использовать все способы раскроя, то общее количество заготовок , при условии, что первым способом раскроено прутков, вторым способам - прутков и т.д., можно выразить суммой: 
. Эта сумма по условию задачи должна равняться 135, т.е.
.
Аналогично составляются условия по заготовкам и :
Количество раскраиваемых прутков не может быть отрицательным, т. е.
Целевая функция, выражающая суммарную величину остатков, составляется с использованием величин остатков по каждому из способов раскроя (см. 5 столбец табл. 2.8):
.
Эта сумма должна быть минимальной. Таким образом, математическая модель задачи построена:
требуется найти план количества раскраиваемых прутков 
, при котором целевая функция 
и который удовлетворяет ограничениям: ,
Сформулируем двойственную модель. Двойственная модель будет иметь три переменные, так как прямая модель содержит три ограничения равенства. Пусть 
оценки стоимости заготовки прутков. Определим оценки стоимости заготовок 
, при которых целевая функция стоимости заготовок 
, и которые удовлетворяют системе ограничений: 
Решим прямую задачу. Модель имеет каноническую форму и все свободные члены положительны. Система ограничений не имеет предпочтительного вида. Поэтому найдем начальный опорный план, составив следующую таблицу 4.9.
Таблица 4.9
|
| 
| 
| 
| 
| 
| 
| |
| 0= | |||||||
| 0= | |||||||
| 0= | |||||||
| =
| -100 | -50 | -50 | -100 |
Будем перебрасывать нули из левого столбца наверх таблицы. Для первого шага исключения возьмем разрешающим первый столбец (в нем есть положительный элемент). Этот столбец исключим из следующей таблицы. Разрешающей строкой будет первая строка. Выполнив преобразования, получим следующую таблицу 4.10.
Таблица 4.10
|
|
|
|
|
|
| |
| =
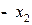
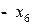
| 67,5 | 0,5 | 0,5 | |||
| 0= | ||||||
| 0= | ||||||
| =
| 6 750 | -50 | -100 |
На втором шаге выбираем разрешающим столбцом четвертый столбец. Этот столбец также исключим из следующей таблицы. Так как
min (180:1=180; 225:2=112,5)=180, то разрешающей строкой будет третья строка. Выполнив преобразования, получим следующую таблицу 4.11.
Таблица 4.11
|
|
|
|
|
| |
| =
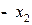
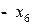
| 67,5 | 0,5 | 0,5 | ||
| 0= | 67,5 | 0,5 | -1,5 | 1,5 | -2 |
| =
| 112,5 | 0,5 | 1,5 | 0,5 | |
| =
| 18 000 |
На третьем шаге выбираем разрешающим столбцом третий столбец. Так как min (67,5:1,5=45; 112,5:0,5=225)=45, то разрешающей строкой будет вторая строка. Выполнив преобразования, получим следующую таблицу 4.12.
Таблица 4.12
| БП |
| СП | ||
|
|
|
| ||
| =
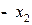
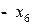
| 67,5 | 0,5 | 0,5 | |
| =
| 
| -1 | 
| |
| =
|
| 
| ||
| =
| 18 000 |
Начальный опорный план найден: 
. Он не является оптимальным, так как в - строке имеются положительные элементы (рассматривается задача минимизации). Выбираем разрешающий столбец по наибольшему элементу в индексной строке – это третий столбец. Разрешающим элементом в нем будет 
, так как он является одним положительным элементом. После шага жорданова исключения приходим к таблице 4.13.
Таблица 4.13
| БП |
| СП | ||
|
|
|
| ||
| =
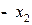
| 67,5 | 
| 0,5 | |
| =
| 87,5 | 0,5 | 0,5 | |
| =
| 33,75 | 
| 
| 
|
| =
| 11 250 | -75 |
В строке целевой функции есть положительный элемент. Следовательно, первый столбец будет разрешающим. После очередного шага жорданова исключения приходим к таблице 4.14, содержащей оптимальный план 
, так как в строке целевой функции нет положительных элементов (задача решается на min).
Таблица 4.14
| БП |
| СП | ||
|
|
|
| ||
| =
| ||||
| =
| ||||
| =
| 16,875 | |||
| =
| 543,75 | -150 | -37,5 | -37,5 |
Значение двойственных оценок определим с учетом соответствия между переменными. При построении взаимно двойственных моделей соответствие между переменными следующее:
↕ ↕ ↕ ↕ ↕ ↕
После решения и введения новых переменных в базис, получим:
Из последней симплексной таблицы находим значения двойственных оценок при условии, что свободные переменные равны нулю, т. е. 
: 
=150, = 37,5, 
= 37,5. Оптимальный план двойственной модели будет иметь вид: 
.
4.3. Теоремы двойственности. Рассмотрим пару взаимно двойственных моделей:
Прямая. Требуется максимизировать функцию
→ max, (4.14)
при ограничениях
, 
, (4.15)
, j = 
Двойственная. Требуется минимизировать функцию
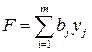→ min, (4.16)
при ограничениях
, j = , (4.17)
, .
Относительно допустимых планов двойственных моделей сформулируем следующие утверждения.
Теорема 4. 1. Для любых допустимых планов
и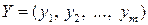 
прямой и двойственной моделей всегда справедливо неравенство:
или 
. (4.18)
Это неравенство называется основным неравенством теории двойственности.
Действительно, умножив неравенство (4.15) на 
и просуммировав по индексу 
, неравенство можно переписать в виде:
. (4.19)
Умножая неравенство (4.17) на и суммируя по индексу 
, получим:
. (4.20)
Поскольку в неравенствах (4.19) и (4.20) левые части равны, то, сравнивая их, получаем основное неравенство теории двойственности (4.18).
С экономической точки зрения, неравенство (4.18) означает, что для любого допустимого плана производства и любого допустимого вектора оценок ресурсов стоимость изготовленного продукта не превосходит оценки ресурсов.
Теорема 4.2. (Достаточный признак оптимальности). Если для некоторых допустимых планов 
и 
пары двойственных задач выполняется равенство 
, то 
– оптимальный план (4.14) – (4.15), а 
– оптимальный план модели (4.16) – (4.17).
Действительно, пусть 
– любой допустимый план задачи (4.14) – (4.15), тогда в силу неравенства (4.18) выполняется неравенство: 
. Но так как по условию 
, то 
. В силу произвольности допустимого плана следует, что 
, т. е. – оптимальный план задачи (4.14) – (4.15).
Пусть теперь 
– любой допустимый план двойственности задачи (4.16)- – (4.17). Из неравенства (4.18) следует, что 
. Но так как , то 
, а поскольку произвольный план, то 
, следовательно – оптимальный план модели (4.16) - (4.17).
Теорема 4.3 (теорема существования оптимальных планов). Для того чтобы прямая и двойственная модели имели оптимальный план, необходимо и достаточно, чтобы для каждой из них существовал хотя один допустимый план.
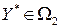Доказательство. Необходимость. Пусть пара двойственных моделей имеет оптимальные планы и : , , 
, 
, 
и 
– множества допустимых решений моделей. Это означает, что множества не пустые, так как имеют хотя бы по одному допустимому плану.
Достаточность. Пусть и – допустимые планы пары двойственных моделей. Рассмотрим допустимый план