Рассмотрим линейнуюоптимизационную модель с системой ограничений, записанной в каноническом виде:
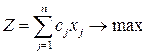 , (2.1)
, (2.1)
 , i =
, i =  ; (2.2)
; (2.2)
 , j =
, j =  . (2.3)
. (2.3)
Система ограничений содержит m уравнений, тогда если:
1) ранг системы r = m=n, т. е. все уравнения линейно независимы и их число равно числу неизвестных, то система имеет единственное решение, и вопрос о выборе оптимального плана отпадает;
2) ранг системы меньше числа неизвестных, т.е. 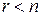 , тогда система имеет бесконечное множество решений и, следовательно, возможен выбор оптимального плана.
, тогда система имеет бесконечное множество решений и, следовательно, возможен выбор оптимального плана.
Поэтому предположим, что 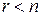 . В этом случае система векторов-столбцов
. В этом случае система векторов-столбцов  , …,
, …,  может содержать несколько базисов. Их число не превосходит
может содержать несколько базисов. Их число не превосходит  . Неизвестные, соответствующие r векторам базиса, называют базисными, а остальные n – r называют свободными неизвестными.
. Неизвестные, соответствующие r векторам базиса, называют базисными, а остальные n – r называют свободными неизвестными.
Если, например, один из базисов составляют первые r векторов  , то базисными будут неизвестные
, то базисными будут неизвестные  , а свободными -
, а свободными - 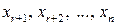 . Тогда систему ограничений (2.2) можно преобразовать к виду:
. Тогда систему ограничений (2.2) можно преобразовать к виду:
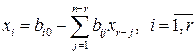 . (2.4)
. (2.4)
Запись (2.4) называют разрешенной формой системы или общим решением.
Базисное решение – частное решение, полученное из общего при нулевых значениях свободных неизвестных:
 .
.
Так как число базисов равно  , то и базисных решений системы (2.2) будет не более
, то и базисных решений системы (2.2) будет не более  . Если в базисном решении все базисные переменные принимают неотрицательные значения, то его называют опорным. Следовательно, опорных планов не более чем
. Если в базисном решении все базисные переменные принимают неотрицательные значения, то его называют опорным. Следовательно, опорных планов не более чем  .
.
План  =(
=( ) задачи (2.2), (2.3) называется опорным, если ненулевым положительным значениям переменных
) задачи (2.2), (2.3) называется опорным, если ненулевым положительным значениям переменных  соответствуют базисные векторы
соответствуют базисные векторы 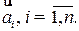
Опорный план не может содержать более чем r положительных компонент. Опорный план, содержащий ровно r отличных от нуля компонент называется невырожденным. Если же хотя бы одна из базисных компонент равна 0, то опорный план называется вырожденным.
Так как планы линейнойоптимизационной модели с геометрической точки зрения – это точки многогранника планов Ω, то опорные планы являются его вершинами.
Итак, каждому опорному плану модели (2.2), (2.3) соответствует вершина многогранника планов и, наоборот, каждой вершине многогранника планов соответствует опорный план модели (2.2), (2.3).
Более того, любой план линейнойоптимизационной модели можно представить как выпуклую линейную комбинацию ее опорных планов. Поэтому для исследования планов линейнойоптимизационной модели достаточно изучить лишь опорные планы.
Опорные планы линейнойоптимизационной модели удовлетворяют теореме.
Теорема 2.1. Если целевая функция линейнойоптимизационной модели достигает экстремального значения в некоторой точке области допустимых решений Ω, то она принимает это значение в угловой (крайней) точке, если же более чем в одной угловой (крайней) точке, то она принимает это же значение в любой их выпуклой линейной комбинации.
Доказательство. Рассмотрим линейнуюоптимизационную модель в канонической форме (2.1) – (2.3). Система ограничений (2.2) определяет многогранник Ω. Следовательно, функция  определена на замкнутом ограниченном множестве, и она достигает наибольшего значения
определена на замкнутом ограниченном множестве, и она достигает наибольшего значения  в некоторой точке
в некоторой точке  Это значит, что для любой точки
Это значит, что для любой точки  . Если
. Если  – угловая точка, то теорема доказана. Пусть
– угловая точка, то теорема доказана. Пусть  – не угловая точка, а угловыми являются точки
– не угловая точка, а угловыми являются точки  . Так как Ω – выпуклое множество, то для любой точки Х n -мерного пространства справедливо равенство:
. Так как Ω – выпуклое множество, то для любой точки Х n -мерного пространства справедливо равенство: 
 . Это равенство будет выполняться и для
. Это равенство будет выполняться и для  :
:
 ,
, 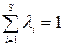 .
.
Так как функция  линейна, то
линейна, то  .
.
Обозначим через 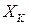 ту из вершин, в которой
ту из вершин, в которой  принимает наибольшее значение:
принимает наибольшее значение: 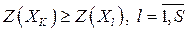 .
.
Тогда,  т. е.
т. е.  Но по условию теоремы
Но по условию теоремы  поэтому это может быть если
поэтому это может быть если  . Следовательно,
. Следовательно,  , тогда
, тогда  , так как
, так как 
Предположим теперь, что 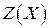 достигает в угловых точках
достигает в угловых точках 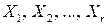 наибольшего значения, равного М, т. е.
наибольшего значения, равного М, т. е. 
Рассмотрим точку Х, являющуюся их линейной комбинацией:
 , (
, ( ).
).
Вычислим значение функции  в точке
в точке 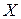 :
:  Значит, целевая функция достигает максимального значения в любой точке множества планов, являющихся линейной комбинацией крайних точек. Теорема доказана.
Значит, целевая функция достигает максимального значения в любой точке множества планов, являющихся линейной комбинацией крайних точек. Теорема доказана.
Геометрически это значит, что гиперплоскость, определяемая целевой функцией, отвечающая наибольшему значению  , проходит через угловую точку, либо через ребро, либо грань многогранника Ω, определяемого системой ограничений (2.2).
, проходит через угловую точку, либо через ребро, либо грань многогранника Ω, определяемого системой ограничений (2.2).
Так как угловой точке соответствует опорный план, то оптимальный план совпадает хотя бы с одним опорным планом линейнойоптимизационной модели. Следовательно, нужно проверить все опорные планы и выбрать тот, при котором  достигает оптимума. Но так как перебор всех опорных планов – процедура длительная, то разработаны методы упорядоченного перебора, позволяющие сократить число испытуемых опорных планов.
достигает оптимума. Но так как перебор всех опорных планов – процедура длительная, то разработаны методы упорядоченного перебора, позволяющие сократить число испытуемых опорных планов.
Симплексный метод
3.1. Понятие о симплексном методе. Симплексный метод (симплекс-метод) является одним из универсальных методов решения линейнойоптимизационной модели. Его называют так же методом последовательного улучшения плана.
Рассмотрим линейнуюоптимизационную модель с системой ограничений в канонической форме записи:
 (3.1)
(3.1)
 , i =
, i =  , (3.2)
, (3.2)
 , j =
, j =  . (3.3)
. (3.3)
Из теоремы: «Линейная функция, определенная на выпуклом n‑мерном многограннике, достигает наибольшего значения в вершине этого многогранника. Если линейная функция достигает наибольшего значения более чем в одной вершине, то она достигает такого же значения в любой точке, являющейся выпуклой линейной комбинацией этих вершин » следует, что оптимальный план задачи (3.1)-(3.3) является одним из опорных решений системы (3.2). Это опорное решение, применяя симплекс-метод, мы и ищем, переходя от одного опорного решения к другому, при условии, что значение функции (3.1) возрастает (не убывает).
Суть метода: предположим, что в системе (3.2) m < n и все m уравнений линейно независимы: r = m < n. Тогда система (3.2) имеет бесконечное множество решений. Разрешаем систему (3.2) относительно базисных неизвестных 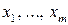 (m < n):
(m < n):
 , j =
, j =  , (3.4)
, (3.4)
и подставляя значения  (3.4) в целевую функцию (3.1), получим:
(3.4) в целевую функцию (3.1), получим:
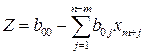 , (3.5)
, (3.5)
 , (3.6)
, (3.6)
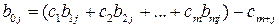 . (3.7)
. (3.7)
Отметим, что значения базисных переменных  и целевой функции
и целевой функции  полностью определяется значениями свободных неизвестных
полностью определяется значениями свободных неизвестных 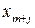 .
.
Пусть в (3.4) все  , тогда план
, тогда план  , полученный при нулевых значениях свободных переменных
, полученный при нулевых значениях свободных переменных 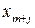 , будет невырожденным опорным, а
, будет невырожденным опорным, а  .
.
Опорный план  соответствует базису
соответствует базису  . Если значение
. Если значение  не оптимальное, то преобразовывают базис Б
не оптимальное, то преобразовывают базис Б  в новый базис Б
в новый базис Б  , удаляя из Б
, удаляя из Б  одну переменную и вводя вместо нее другую из свободных неизвестных, так чтобы
одну переменную и вводя вместо нее другую из свободных неизвестных, так чтобы  , где
, где  – опорный план в новом базисе Б
– опорный план в новом базисе Б  . Преобразовывая один базис в другой, переходят от одного опорного плана к другому, и так как число опорных планов не более
. Преобразовывая один базис в другой, переходят от одного опорного плана к другому, и так как число опорных планов не более 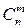 , то через конечное число шагов, либо приходят к базису
, то через конечное число шагов, либо приходят к базису  , в котором
, в котором  достигает оптимума и тогда
достигает оптимума и тогда 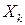 – оптимальный, либо устанавливают, что задача (3.1) - (3.3) неразрешима.
– оптимальный, либо устанавливают, что задача (3.1) - (3.3) неразрешима.
С геометрической точки зрения, перебор опорных планов  можно рассматривать как последовательный переход из одной вершины многогранника планов к смежной, в которой значение целевой функции не меньше, чем в предыдущей вершине.
можно рассматривать как последовательный переход из одной вершины многогранника планов к смежной, в которой значение целевой функции не меньше, чем в предыдущей вершине.
3.2. Построение начального опорного плана. Первым шагом симплексного метода является построение начального опорного плана. Для этого систему ограничений приводят к предпочтительному виду. Система ограничений имеет предпочтительный вид, если:
1) ограничения заданы в виде равенств;
2) правые части (системы ограничений) (3.2) неотрицательны, т. е.  ;
;
3) если левая часть ограничения равенства содержит переменную, входящую с коэффициентом, равным единице, то в остальные ограничения равенства эта переменная входит с коэффициентом, равным нулю.
Например, в системе ограничений:
 ,
,
 ,
,
 .
.
первое и второе ограничения имеют предпочтительный вид, третье – нет.
Если каждое ограничение (3.2) имеет предпочтительный вид, то ее опорное решение (базисное с неотрицательными координатами) строится следующим образом: все переменные, кроме предпочтительных, приравниваются к нулю. Тогда предпочтительные переменные будут равны правым частям. Полученный план будет иметь не более m отличных от нуля координат (число ненулевых координат равно рангу системы ограничений) и полученный план будет опорным. Предпочтительные переменные – это базисные переменные, другие переменные, которые приравниваем нулю – это свободные неизвестные.
Как же приводится система ограничений к предпочтительному виду?
1) Если система ограничений имеет вид:
 ,
, 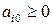 ,
,  ,
,
то прибавив к левым частям дополнительные переменные 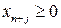 ,
,  , получим расширенную задачу, эквивалентную данной. В расширенной задаче система ограничений:
, получим расширенную задачу, эквивалентную данной. В расширенной задаче система ограничений:
 ,
, 
имеет предпочтительный вид. Начальный опорный план имеет вид:
 =
=  .
.
В целевую функцию дополнительные переменные вводятся с коэффициентами равными нулю: 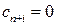 ,
,  .
.
2) Если система ограничений имеет вид:
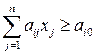 ,
, 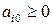 ,
,  ,
,
то вычитая из левых частей неотрицательные дополнительные переменные 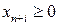 ,
,  , получим расширенную задачу, эквивалентную данной. Полученная система ограничений не имеет предпочтительного вида, так как дополнительные переменные входят в левую часть с коэффициентами «–1». План
, получим расширенную задачу, эквивалентную данной. Полученная система ограничений не имеет предпочтительного вида, так как дополнительные переменные входят в левую часть с коэффициентами «–1». План  недопустим. Поэтому вводят искусственный базис. К левым частям системы ограничений - равенств, не имеющих предпочтительного вида, добавляют искусственные переменные
недопустим. Поэтому вводят искусственный базис. К левым частям системы ограничений - равенств, не имеющих предпочтительного вида, добавляют искусственные переменные  . В целевую функцию
. В целевую функцию  вводят с коэффициентом, равным (+ М) в случае решения задачи на минимум, и с коэффициентом равным (– М) на максимум, где М – большое положительное число. Полученная задача называется М -задачей, она имеет предпочтительный вид и стратегически эквивалентна исходной.
вводят с коэффициентом, равным (+ М) в случае решения задачи на минимум, и с коэффициентом равным (– М) на максимум, где М – большое положительное число. Полученная задача называется М -задачей, она имеет предпочтительный вид и стратегически эквивалентна исходной.
3) Если исходная линейнаяоптимизационная модели имеет вид:
 (3.8)
(3.8)
 ,
,  ,
, 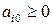 ; (3.9)
; (3.9)
 , j =
, j =  ,
,
и если ни одно из ограничений не имеет предпочтительного вида, то М ‑ модель запишется в виде:

 ; (3.10)
; (3.10)
 ,
,  ; (3.11)
; (3.11)
 , j =
, j =  ,
,  ,
,  ; (3.12)
; (3.12)
где знак «–» в (3.10) относится к модели на максимум. Начальный опорный план М ‑задачи, которая имеет предпочтительный вид, запишется:
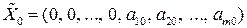 .
.
Если в оптимальном плане М ‑ модели:  все искусственные переменные равны нулю, то план
все искусственные переменные равны нулю, то план

Является оптимальным для исходной модели. Если же хотя бы одна из искусственных переменных  отлична от нуля, то система ограничений исходной модели несовместна.
отлична от нуля, то система ограничений исходной модели несовместна.
Так как исходную модель можно представить в предпочтительном виде, то будем считать, что линейнаяоптимизационная модель имеет предпочтительный вид:
 ; (3.13)
; (3.13)
 ,
,  ,
,  ; (3.14)
; (3.14)
 , j =
, j =  . (3.15)
. (3.15)
Разрешая систему (3.14) относительно базисных переменных  , подставляем в (3.13), получим (3.5). Из (3.5)-(3.7) можно выяснить признак оптимальности опорного плана. Из (3.14) находим начальный опорный план
, подставляем в (3.13), получим (3.5). Из (3.5)-(3.7) можно выяснить признак оптимальности опорного плана. Из (3.14) находим начальный опорный план  , а из (3.13) значение целевой функции:
, а из (3.13) значение целевой функции:
 , где
, где  .
.
Так как  , j =
, j =  , то при
, то при 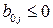 целевая функция достигает минимального значения в точке
целевая функция достигает минимального значения в точке  . Если же
. Если же  , то в
, то в  целевая функция достигает max:
целевая функция достигает max:  . Это видно из равенства
. Это видно из равенства 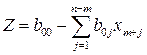 .
.
Для решения линейнойоптимизационной модели вручную условия заносят в таблицу, которая называется симплексной. Перед заполнением таблицы систему ограничений приводят к эквивалентному предпочтительному виду. В столбце БП записываются базисные переменные (т.е. предпочтительные) для каждого из ограничений равенств, в столбец  - свободные члены системы ограничений в предпочтительном виде. Затем записываем свободные переменные (СП) со знаком минус. На пересечении строк и столбцов записываются коэффициенты системы ограничений. Последнюю строку, называемой индексной строкой (строкой целевой функции), заполняют коэффициентами целевой функции со знаком минус. Исходная симплексная таблица имеет вид:
- свободные члены системы ограничений в предпочтительном виде. Затем записываем свободные переменные (СП) со знаком минус. На пересечении строк и столбцов записываются коэффициенты системы ограничений. Последнюю строку, называемой индексной строкой (строкой целевой функции), заполняют коэффициентами целевой функции со знаком минус. Исходная симплексная таблица имеет вид:
Таблица 3.1
| БП | 
| СП |
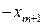 … …  … … 
| ||
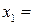
| 
|  … …  … … 
|
| … | … | ... |

| 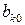
| 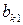 … …  … … 
|
| … | … | ... |

| 
|  … …  … … 
|
 = =
| 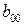
|  … …  … … 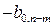
|
 ,
,  ,
,  ,
,  ;
;
или
 ,
, 
 ,
, 
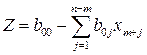 .
.
3.3. Признак оптимальности опорного плана. Снова рассмотрим линейную оптимизационную модель в предпочтительном виде:
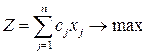
 ,
,  ,
,  ;
;
 , j =
, j =  .
.
Пусть эта задача решается на максимум. Начальный опорный план  , значение целевой функции:
, значение целевой функции: 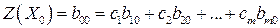 .
.
Если для всех j  , то целевая функция достигает максимума и
, то целевая функция достигает максимума и  − оптимальный план. Предположим, что существуют отрицательные значения
− оптимальный план. Предположим, что существуют отрицательные значения  . Пусть их несколько. Тогда выбираем наибольшее по модулю, из отрицательных
. Пусть их несколько. Тогда выбираем наибольшее по модулю, из отрицательных  , которое обозначим
, которое обозначим  . Столбец
. Столбец  назовем разрешающим. Соответствующую переменную
назовем разрешающим. Соответствующую переменную  введем в базис. Выбирая переменную, вводимую в базис (или выбирая разрешающий столбец) по наименьшему отрицательному элементу индексной
введем в базис. Выбирая переменную, вводимую в базис (или выбирая разрешающий столбец) по наименьшему отрицательному элементу индексной  - строки, обеспечивается не убывание целевой функции.
- строки, обеспечивается не убывание целевой функции.
Для определения переменной, подлежащей исключению из базиса, составляются отношения свободных членов к положительным элементам разрешающего столбца (такие отношения называются симплексными). Наименьшее симплексное отношение и определяет строку (разрешающую), содержащую исключаемую переменную. Выбор переменной, исключаемой из базиса, но min симплексному отношению гарантирует положительность базисных компонент в новом опорном плане.
Значение новой базисной переменной 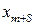 в новом опорном плане будет равно
в новом опорном плане будет равно  . Численные значения остальных базисных переменных в новом опорном плане и соответствующее значение функции цели
. Численные значения остальных базисных переменных в новом опорном плане и соответствующее значение функции цели  находятся после того, как измененная система базисных переменных
находятся после того, как измененная система базисных переменных 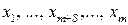 будет выражена через измененную систему свободных переменных
будет выражена через измененную систему свободных переменных  .
.
Установим правила, по которым осуществляется преобразование условий модели от одного базиса к другому. В каждом уравнении системы ограничений, где коэффициент 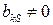 при переменной
при переменной 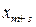 , выделим слагаемое содержащее неизвестное
, выделим слагаемое содержащее неизвестное 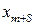 :
:

Затем  - тое уравнение разрешаем относительно
- тое уравнение разрешаем относительно 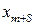 :
:
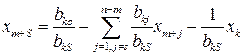 (3.16)
(3.16)
и подставляем (3.16) во все остальные уравнения системы ограничений. Коэффициент 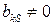 при
при 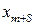 в уравнении (3.16) называют разрешающим элементом. В равенстве (3.16) новая базисная переменная выражена через свободные переменные, среди которых находится и бывшая базисная переменная
в уравнении (3.16) называют разрешающим элементом. В равенстве (3.16) новая базисная переменная выражена через свободные переменные, среди которых находится и бывшая базисная переменная  .
.
Подставив (3.16) во все остальные уравнения системы ограничений, выражаем через новый набор свободных переменных остальные базисные переменные. Выполнив преобразования, получим:
 (3.17)
(3.17)
Обозначив  , i = 0, 1, 2, …, m, i ≠ k; j = 0, 1, …, n – m, j ≠ s,
, i = 0, 1, 2, …, m, i ≠ k; j = 0, 1, …, n – m, j ≠ s,
получим следующую систему равенств:
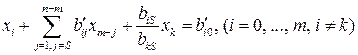 . (3.18)
. (3.18)
Приведение системы
 ,
,  ,
,  ,
,
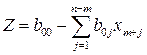
к новому базису называется симплексным преобразованием. В результате получим симплексную таблицу 3.2:
Таблица 3.2
| БП | 
| СП |
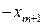 … … 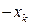 … … 
| ||
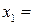
| 
|  … …  … … 
|
| … | … | ... |

| 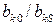
| 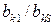 … …  … … 
|
| … | … | ... |

| 
|  … …  … … 
|
 = =
| 
|  … …  … … 
|
Полагая в равенствах (3.16) и (3.18) свободные переменные  равными нулю, получим компоненты нового опорного плана
равными нулю, получим компоненты нового опорного плана  и новое значение целевой функции
и новое значение целевой функции 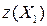 :
:
 ,
,  .
.
Сформулируем правила перехода к новому опорному плану:
1) выбираем разрешающий элемент 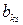 , стоящий на пересечении разрешающей строки и разрешающего столбца;
, стоящий на пересечении разрешающей строки и разрешающего столбца;
2) разрешающий элемент заменяем обратной величиной  ;
;
3) остальные элементы разрешающей строки 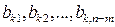 делим на разрешающий элемент
делим на разрешающий элемент 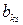 :
:  ,
,  ;
;
4) остальные элементы разрешающего столбца  делим на разрешающий элемент
делим на разрешающий элемент 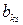 и меняем знаки;
и меняем знаки;
5) все другие элементы симплексной таблицы вычисляются по правилу прямоугольника, вершинами которого служат разрешающий 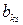 и преобразуемый
и преобразуемый  элементы (они образуют главную диагональ) и два других элемента (они образуют побочную диагональ), составляющих прямоугольник:
элементы (они образуют главную диагональ) и два других элемента (они образуют побочную диагональ), составляющих прямоугольник:  .
.
Таким образом, симплекс-метод представляет собой процесс направленного решения системы линейных уравнений – ограничений задачи с особым правилом выбора разрешающего элемента, обеспечивающим движение по опорным решениям (правило выбора разрешающей строки) и монотонный рост линейной функции цели (правило выбора разрешающего столбца).
Сформулируем теоремы, в которых определяются условия оптимальности планов, бесконечности оптимальных планов, неограниченности целевой функции.
Теорема 3.1. Если для некоторого опорного плана, при решении модели на максимум, все элементы в индексной строке последней симплексной таблицы неотрицательны, то такой план оптимальный.
Теорема 3.2. Если для некоторого опорного плана, при решении модели на минимум, все элементы в индексной строке последней симплексной таблицы неположительны, то такой план оптимальный.
Теорема 3.3. Если в индексной строке последней симплексной таблицы, содержащей оптимальный план, имеется хотя бы один нулевой элемент, соответствующий свободной переменной, то линейная оптимизационная модель имеет бесконечное множество оптимальных планов; если же все элементы положительны, то оптимальный план единственный.
Теорема 3.4. Если в индексной строке симплексной таблицы, при решении модели на максимум, имеется отрицательный элемент, а в соответствующем столбце нет ни одного положительного элемента, то целевая функция не ограничена сверху на множестве допустимых планов.
Теорема 3.5. Если в индексной строке симплексной таблицы, при решении модели на минимум, имеется положительный элемент, а в соответствующем столбце нет ни одного положительного элемента, то целевая функция не ограничена снизу на множестве допустимых планов.
Пример 3.1. Предприятие может изготовлять четыре вида продукции П  , П
, П  , П
, П  , П
, П  . Сбыт любого ее объема обеспечен. Предприятие располагает в течение квартала трудовыми ресурсами в 100 чел, полуфабрикатами массой 260кг, станочным оборудованием в 370 станко - смен. Нормы ресурсов и прибыль от единицы каждого вида продукции представлены в таблице 3.3:
. Сбыт любого ее объема обеспечен. Предприятие располагает в течение квартала трудовыми ресурсами в 100 чел, полуфабрикатами массой 260кг, станочным оборудованием в 370 станко - смен. Нормы ресурсов и прибыль от единицы каждого вида продукции представлены в таблице 3.3:
Таблица 3.3
| Ресурсы | Продукция | Объем ресурсов | |||
П 
| П 
| П 
| П 
| ||
| Трудовые ресурсы, чел. | 2,5 | 2,5 | 1,5 | ||
| Полуфабрикаты, кг | |||||
| Станочное оборудование, станко-смен | |||||
| Прибыль от единицы продукции, руб. |
max 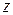
|
Необходимо:
1) определить план выпуска продукции, максимизирующий прибыль;
2) решить задачу с требованием комплектации, чтобы количество единиц третьей продукции было в 3 раза больше количества единиц первой;
3) выяснить оптимальный ассортимент при дополнительных ограничениях: первого продукта выпускать не менее 25 единиц, третьего – не более 30, второго и четвертого – в отношении 1: 3.
Решение. Построим математическую модель задачи. Пусть  , - неизвестные, характеризующие количество выпускаемой продукции предприятием. Требуется определить план
, - неизвестные, характеризующие количество выпускаемой продукции предприятием. Требуется определить план  , при котором предприятие получит максимум прибыли, т. е. целевая функция
, при котором предприятие получит максимум прибыли, т. е. целевая функция
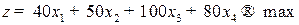 .
.
План удовлетворяет ограничениям:
а) на трудовые ресурсы:
 ;
;
на полуфабрикаты:
 ;
;
на станочное оборудование:
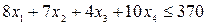 ;
;
условия неотрицательности:
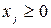 , j =
, j = 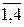 ;
;
б) дополнительное условие комплектации:
 ;
;
в) дополнительные условия:
 .
.
Приведем вначале систему ограничений к предпочтительному виду, добавив к левым частям дополнительные переменные 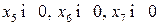 . Получим расширенную задачу, эквивалентную данной.
. Получим расширенную задачу, эквивалентную данной.
В расширенной задаче система ограничений



имеет предпочтительный вид. В целевую функцию дополнительные переменные вводятся с коэффициентами равными нулю:  .
.
Заносим условия расширенной задачи в симплексную таблицу 3.4:
Таблица 3.4
| БП | А 
| СП | |||

| 
| 
| 
| ||

| 2,5 | 2,5 | 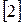
| 1,5 | |

| |||||

| |||||
Функция 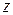
| -40 | -50 | -100 | -80 |
Рассчитаем элементы индексной строки:
 – произведение вектора коэффициентов целевой функции, стоящих у базисных переменных
– произведение вектора коэффициентов целевой функции, стоящих у базисных переменных  = (0, 0, 0) и вектора свободных членов у системы ограничений в предпочтительном виде А
= (0, 0, 0) и вектора свободных членов у системы ограничений в предпочтительном виде А  = (100, 260, 370).
= (100, 260, 370).
Так как  - строка содержит 4 отрицательных элемента, то в базис будем вводить переменную
- строка содержит 4 отрицательных элемента, то в базис будем вводить переменную  , которая соответствует наименьшему значению
, которая соответствует наименьшему значению  ,
, 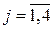 :
:  = - 100. Разрешающим столбцом будет третий столбец.
= - 100. Разрешающим столбцом будет третий столбец.
Для определения переменной, подлежащей исключению из базиса, составляем отношения свободных членов к положительным элементам разрешающего столбца. В разрешающем столбце все элементы положительные: 100/2 =50; 260/4 = 65; 370/4 = 92,5. Выбираем наименьшее, которое определяет первую строку в качестве разрешающей.
Таким образом, разрешающим элементом будет «2». Строим новую симплексную таблицу 3.5:
Таблица 3.5
| БП | 
| СП | |||

| 
| 
| 
| ||

| 1,25 | 1,25 | 1/2 | 0,75 | |

| -1 | -2 | 
| ||

| -2 | ||||
 -строка -строка
| -5 |
 -строка содержит один о
-строка содержит один о