6.3.1.Общие понятия статистических игр. Изучая матричные игры, мы предполагали, что каждый из игроков (участников) стремится к наилучшему для себя результату. На практике же встречаются игры, ситуации, когда один из игроков безразличен к результату игры. Например, управление производственными процессами осуществляется путем реализации последовательности принимаемых решений. Для принятия эффективных решений необходима информация о состоянии объекта управления. С целью уменьшения неблагоприятных последствий в каждом конкретном случае следует учитывать степень риска. В приведенном примере, лицо (или группу лиц), принимающее решение, вступает в игровые отношения с некоторым абстрактным участником игры. В качестве такого игрока выступает «природа». Под природой понимается комплекс внешних обстоятельств (условий), при которых приходится принимать решение. В такой ситуации игрока (группу лиц, объединенных общностью цели) называют статистиком, а игры, в которых одним из участников является человек (игрок А), а другим природа (игрок  ), называются статистическими. Ясно, что природа развивается по объективным законам, независимо от человека, который не всегда знает или знает не полно эти законы. Поэтому, принимая решения, человек должен учитывать их последствия. Любую хозяйственную деятельность человека можно рассматривать как игру с природой.
), называются статистическими. Ясно, что природа развивается по объективным законам, независимо от человека, который не всегда знает или знает не полно эти законы. Поэтому, принимая решения, человек должен учитывать их последствия. Любую хозяйственную деятельность человека можно рассматривать как игру с природой.
Как и в матричных играх, игрок А может использовать стратегии  ,
,  , …,
, …,  . Множество состояний природы
. Множество состояний природы  назовем множеством стратегий
назовем множеством стратегий 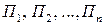 , имея в виду полную совокупность внешних условий, в которых статистику А приходится выбирать свою стратегию. Статистику А обычно известны возможности состояния природы
, имея в виду полную совокупность внешних условий, в которых статистику А приходится выбирать свою стратегию. Статистику А обычно известны возможности состояния природы  , а иногда вероятности
, а иногда вероятности  с которыми она реализует эти состояния. Эти вероятности называются априорными. Проводя эксперименты, статистик может уточнить состояния
с которыми она реализует эти состояния. Эти вероятности называются априорными. Проводя эксперименты, статистик может уточнить состояния  и их вероятности
и их вероятности  , которые называются апостериорными.
, которые называются апостериорными.
Мы рассмотрим статистические игры без эксперимента.
Статистик в своих взаимоотношениях с природой может пользоваться как чистыми стратегиями 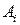 , так и смешанными:
, так и смешанными:
 ,
, 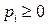 ,
, 
Если статистику А известны числа  , характеризующие пару стратегий (
, характеризующие пару стратегий (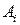 ,
,  ), то статистическую игру можно задать платежной матрицей
), то статистическую игру можно задать платежной матрицей  .
.
Пример 6.6. В фирме «Плюс» при производстве продукции потребляется 20-22 единицы сырья S, в зависимости от его качества. Если для выпуска запланированной продукции сырья окажется недостаточно, то запас его можно пополнить, но одна единица сырья при этом будет стоить 10 ден. ед. Если же запас сырья будет большим, то на хранение и содержание единицы сырья нужно затратить 7 ден.ед.
Придадим описанной ситуации игровую схему. В качестве статистика (игрок А) выступает администрация предприятия, которая может заказать 20, 21 или 22 единицы сырья (стратегии  ,
,  ,
,  ). Вторым игроком (природа
). Вторым игроком (природа  ) может выступать фактический расход сырья в процессе производства. Расход сырья зависит от качества сырья и составляет 20, 21 или 22 единицы сырья (состояния природы
) может выступать фактический расход сырья в процессе производства. Расход сырья зависит от качества сырья и составляет 20, 21 или 22 единицы сырья (состояния природы  ,
,  ,
,  ). Элементы матрицы
). Элементы матрицы  характеризуют дополнительные затраты, вызванные доставкой сырья в случае недостатка или хранением в случае избытка.
характеризуют дополнительные затраты, вызванные доставкой сырья в случае недостатка или хранением в случае избытка.
Паре стратегий ( ,
,  ) соответствует число
) соответствует число  = 0, так как расход и закупка сырья равны.
= 0, так как расход и закупка сырья равны.
Паре стратегий ( ,
,  ) соответствует число
) соответствует число 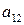 = –10, так как расход превысит запасы и нужно закупить одну единицу сырья.
= –10, так как расход превысит запасы и нужно закупить одну единицу сырья.
Паре стратегий ( ,
,  ) соответствует число
) соответствует число  = –20, закупить нужно 2 единицы сырья.
= –20, закупить нужно 2 единицы сырья.
Паре стратегий ( ,
,  ) соответствует число
) соответствует число  = –7, так как придется хранить 1 единицу сырья, что вызовет затраты 7 ден. ед. и т.д.
= –7, так как придется хранить 1 единицу сырья, что вызовет затраты 7 ден. ед. и т.д.
Таким образом, рассматриваемую ситуацию можно описать при помощи платежной матрицы:
| 
|

| ||
П  (20) (20)
| П  (21) (21)
| П  (22) (22)
| ||
А  (20) (20)
| –10 | –20 | –20 | |
А  (21) (21)
| –7 | –10 | –10 | |
А  (22) (22)
| –14 | –7 | –0 | –14 |

| -10 |
Данная игра не имеет решения в чистых стратегиях, так как  .
.
6.3.2. Правила выбора оптимальной стратегии. Перед выбором оптимальной стратегии статистической игры, упрощают платежную матрицу, пользуясь доминированием стратегий статистика. Доминированием стратегий природы пользоваться нельзя, так как состояние природы объективно, независимо от того, выгодно оно статистику или нет. После упрощения платежной матрицы переходят к матрице рисков, которая позволит выявить преимущество одной стратегии по сравнению с другой при данном состоянии природы. Например, если  , то это не означает, что строка
, то это не означает, что строка  лучше строки
лучше строки  , так как состояние
, так как состояние  может быть более благоприятным для статистика, чем
может быть более благоприятным для статистика, чем  . Эту ситуацию может прояснить анализ матрицы рисков.
. Эту ситуацию может прояснить анализ матрицы рисков.
Риском  статистика, когда он пользуется чистой стратегией
статистика, когда он пользуется чистой стратегией 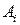 при состоянии
при состоянии  природы, называем разность между максимальным выигрышем
природы, называем разность между максимальным выигрышем  , который статистик мог бы получить, достоверно зная, что природой будет реализовано состояние
, который статистик мог бы получить, достоверно зная, что природой будет реализовано состояние  , и тем выигрышем
, и тем выигрышем  , который он получит, используя стратегию
, который он получит, используя стратегию 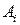 , не зная, какое из состояний
, не зная, какое из состояний  реализует природа.
реализует природа.
Таким образом,  (
( – максимальный элемент j -го столбца). Матрица рисков:
– максимальный элемент j -го столбца). Матрица рисков:

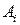
|  … … 
|

|

|  … … 
| 
|
| …. | … … … | … |

|  … … 
| 
|

|  … … 
|
Матрица рисков для рассматриваемого примера:
 
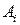
| 
| 
| 
|

|  = 0 = 0
|  = 10 = 10
|  = 20 = 20
|

|  = 7 = 7
|  = 0 = 0
|  = 10 = 10
|

|  = 14 = 14
|  = 7 = 7
|  = 0 = 0
|
Рассмотрим критерии выбора оптимальной стратегии статистика с использованием вероятностей  состояния природы. В критериях используют:
состояния природы. В критериях используют:
– среднее значение  выигрыша:
выигрыша:
 =
=  ; (6.14)
; (6.14)
определяется для каждой чистой стратегии  ,...,
,...,  ;
;
– среднее значение 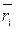 риска:
риска:
 =
=  , (6.15)
, (6.15)
которое находят по матрице рисков.
Критерий Байеса. Оптимальной считается стратегия 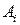 , при которой максимизируется средний выигрыш
, при которой максимизируется средний выигрыш  статистика, т. е. обеспечивается max
статистика, т. е. обеспечивается max  ,
,  .
.
Вернемся к рассматриваемому примеру и предположим, что вероятности  ,
,  ,
,  потребления сырья в количествах 20, 21 и 22 единиц соответственно равны 0,3; 0,2; и 0,5. Используя формулу (6.14), находим
потребления сырья в количествах 20, 21 и 22 единиц соответственно равны 0,3; 0,2; и 0,5. Используя формулу (6.14), находим  =
=  значение средних выигрышей. Составим таблицу:
значение средних выигрышей. Составим таблицу:
 
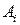
|   
| 
|

| 0 –10 –20 | –7,0 |

| –7 0 –10 | –7,1 |

| –14 –7 0 | –5,6 |

| 0,3 0,2 0,5 |
Из таблицы видим, что максимальной величины «–5,6» средний выигрыш достигает при стратегии  , которая предусматривает запасать 22 единицы сырья. Оптимальной стратегий будет стратегия
, которая предусматривает запасать 22 единицы сырья. Оптимальной стратегий будет стратегия  (по Байесу).
(по Байесу).
Вычислим среднее значение рисков по формуле (6.15), и составим матрицу рисков:
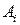
|   
| 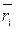
|

| 0 10 20 | 7,0 |

| 7 0 10 | 7,1 |

| 14 7 0 | 5,6 |

| 0,3 0,2 0,5 |
В этом случае риск нужно минимизировать. Минимальный риск  соответствует стратегии
соответствует стратегии  .
.
Из примера следует, что стратегия, максимизирующая средний выигрыш, совпадает со стратегией, минимизирующей средний риск.
Критерий Лапласа. Если статистик А не располагает определенными вероятностями  , …,
, …,  состояний природы
состояний природы  , то их вероятности полагают равными, т. е.
, то их вероятности полагают равными, т. е.  =
=  = … =
= … =  =
=  . Оптимальной считают такую стратегию, при которой обеспечивается
. Оптимальной считают такую стратегию, при которой обеспечивается  =
=  .
.
Если состояние природы можно оценить по степени их правдоподобия, то вероятности реализации состояний  считают пропорциональными членам убывающей арифметической прогрессии:
считают пропорциональными членам убывающей арифметической прогрессии:

и значения  определяют по формуле:
определяют по формуле:
 j = 1, 2, …, n.
j = 1, 2, …, n.
Если вероятности состояний природы неизвестны, то для выбора оптимальной стратегии статистика можно использовать критерий Вальда.
Критерий Вальда. С татистик выбирает такую чистую стратегию 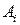 , при которой наименьший выигрыш
, при которой наименьший выигрыш  будет максимальным, т.е. обеспечивается максимин:
будет максимальным, т.е. обеспечивается максимин:

так как статистик исходит из предложения, что природа действует против него наихудшим образом.
Для рассматриваемого примера:
 .
.
Следовательно, оптимальной по Вальду будет стратегия  , так как запас сырья на предприятии должен составлять 21 единицу, при этом дополнительные затраты будут равны 7 ед.
, так как запас сырья на предприятии должен составлять 21 единицу, при этом дополнительные затраты будут равны 7 ед.
Оптимальной смешанной стратегией статистика по критерию Вальда считают ту, при которой его минимальный средний выигрыш  будет max. Смешанная стратегия находится из условия
будет max. Смешанная стратегия находится из условия  .
.
Для рассматриваемого примера оптимальная по Вальду смешанная стратегия  определяется решением линейной оптимизационной модели:
определяется решением линейной оптимизационной модели:
 ;
;

Решение в смешанных стратегиях целесообразнее, чем в чистых стратегиях.
Критерий Сэвиджа. Оптимальной чистой стратегией будет та чистая стратегия 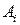 , при которой минимизируется величина
, при которой минимизируется величина  максимального риска, т. е. достигается
максимального риска, т. е. достигается  .
.
Для нашего примера:
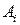
|   
| 
|

| 0 10 20 | |

| 7 0 10 | |

| 14 7 0 |
оптимальной по Сэвиджу будет чистая стратегия  , так как
, так как
 .
.
Оптимальной смешанной стратегией по критерию Сэвиджа считают ту смешанную стратегию  , при которой максимальное значение среднего риска минимизируется, т. е. обеспечивается выполнение условия:
, при которой максимальное значение среднего риска минимизируется, т. е. обеспечивается выполнение условия:
 .
.
Критерий Гурвица. Оптимальной чистой стратегией будет та чистая стратегия, для которой  , где
, где 
 (0; 1) и выбирается из субъективных соображений.
(0; 1) и выбирается из субъективных соображений.
При  = 1 критерий Гурвица превращает в критерий Вальда:
= 1 критерий Гурвица превращает в критерий Вальда:  ; при
; при  = 0 – в критерий крайнего оптимизма:
= 0 – в критерий крайнего оптимизма:  ; при
; при  получаем критерий пессимизма-оптимизма. Значение
получаем критерий пессимизма-оптимизма. Значение  выбирают исходя из опыта или из субьективных соображений.
выбирают исходя из опыта или из субьективных соображений.
Положив в нашем примере  = 0,7, получим:
= 0,7, получим:
 .
.
Все результаты приведены в таблице.
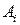
|   
| 
| 0,7 
| 
| 0,3 
| 
|

| 0 10 20 | –20 | –14 | –14 | ||

| 7 0 10 | –10 | –7 | –7 | ||

| 14 7 0 | –14 | –9,8 | –9,8 |
Из последнего столбца следует, что оптимальной стратегией является чистая стратегия  .
.
В заключение подчеркнем, что выбор чистой стратегии следует проводить по нескольким критериям. Решение статистической игры по рассмотренным критериям позволяет более обоснованно принимать ту стратегию, которая гарантирует статистику больший выигрыш.
Тест № 3
1. Игра – это
1) конфликтная ситуация;
2) ситуация, подчиненная определенным правилам;
3) математическая модель конфликтной ситуации.
2. Матричная игра – это игра
1) двух лиц;
2) трех лиц;
3) множества лиц.
3. Если стратегии игрока А представлены в платежной матрице строками, а стратегии игрока В – столбцами, то элемент матрицы, стоящий на пересечении выбранных строки и столбца, определяет
1) суммарный выигрыш игроков А и В;
2) суммарный проигрыш игроков А и В;
3) выигрыш игрока А;
4) проигрыш игрока А.
4. Стратегия игрока А называется оптимальной, если при ее применении
1) выигрыш игрока А уменьшается в зависимости от того, какой стратегией пользуется игрок В;
2) выигрыш игрока А увеличивается в зависимости от того, какой стратегией пользуется игрок В;
3) выигрыш игрока А не увеличивается, какими бы стратегиями ни пользовался игрок В;
4) выигрыш игрока А не уменьшается, какими бы стратегиями ни пользовался игрок В.
5. Стратегия игрока В называется оптимальной, если при ее применении
1) проигрыш игрока В уменьшается в зависимости от того, какой стратегией пользуется игрок А;
2) проигрыш игрока В увеличивается в зависимости от того, какой стратегией пользуется игрок А;
3) проигрыш игрока В не увеличивается, какими бы стратегиями ни пользовался игрок А;
4) проигрыш игрока В не уменьшается, какими бы стратегиями ни пользовался игрок А.
6. Нижняя чистая цена игры показывает
1) какой минимальный выигрыш может получить игрок А, применяя свои чистые стратегии при любых действиях игрока В;
2) какой средний выигрыш может получить игрок А, применяя свои чистые стратегии при любых действиях игрока В;
3) какой максимальный выигрыш может получить игрок А, применяя свои чистые стратегии при любых действиях игрока В.
7. Верхняя чистая цена игры показывает
1) какой минимальный проигрыш может быть у игрока В при любых действиях игрока А;
2) какой средний проигрыш может быть у игрока В при любых действиях игрока А;
3) какой максимальный проигрыш может быть у игрока В при любых действиях игрока А.
8. В матричной игре смешанной стратегией игрока является
1) вероятность применения одной из его чистых стратегий;
2) набор вероятностей применения нескольких чистых стратегий;
3) полный набор вероятностей применения его чистых стратегий.
9. В матричной игре активные стратегии - это
1) чистые стратегии игрока, входящие в оптимальную смешанную стратегию с вероятностями, отличными от нуля;
2) чистые стратегии игрока, входящие в оптимальную смешанную стратегию с любыми вероятностями;
3) любые стратегии игрока, применяемые им с целью увеличения выигрыша.
10. Стратегия  доминирует над стратегией
доминирует над стратегией  , если
, если
1) элементы k -й строки не меньше соответствующих элементов s -ой строки:  ,
,  ;
;
2) элементы k -й строки не больше соответствующих элементов s -ой строки:  ,
,  ;
;
3) элементы k -й строки меньше соответствующих элементов s -ой строки:  ,
,  ;
;
4) элементы k -й строки больше соответствующих элементов s -ой строки:  ,
,  .
.
11. Стратегия  доминирует над стратегией
доминирует над стратегией 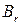 , если
, если
1) элементы l -го столбца больше соответствующих элементов r -го столбца:  ,
,  ;
;
2) элементы l -го столбца не больше соответствующих элементов r -го столбца:  ,
,  ;
;
3) элементы l -го столбца не меньше соответствующих элементов r -го столбца: 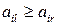 ,
,  ;
;
4) элементы l -го столбца меньше соответствующих элементов r -го столбца:  ,
,  .
.
12. В статистических играх риск - это
1) максимальный выигрыш игрока;
2) минимальный выигрыш игрока;
3) разность между максимальным выигрышем игрока для каждого состояния природы и его реальным выигрышем.
13. При использовании критерия Байеса оптимальной считается стратегия 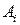 , при которой
, при которой
1) минимизируется средний выигрыш  статистика;
статистика;
2) максимизируется средний выигрыш  статистика;
статистика;
3) остается неизменным средний выигрыш  статистика.
статистика.
14. При использовании критерия Лапласа оптимальной считают такую стратегию, при которой обеспечивается
1)  =
=  ;
;
2)  =
= 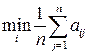 .
.
15. При использовании критерия Вальда (критерия крайнего пессимизма) оптимальной считается стратегия, при которой обеспечивается
1)  ;
;
2)  ;
;
3)  .
.
16. При использовании критерия Сэвиджа оптимальной считается стратегия, при которой достигается
1) 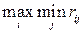 ;
;
2)  ;
;
3)  ;
;
4) 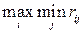 .
.
17. Значение параметра  в критерии Гурвица
в критерии Гурвица
1) является стандартной величиной;
2) рассчитывается по определенным правилам;
3) задается, принимающим решение, на основании опыта.