Множества
1.1. Решить задачу.
На экзамене по математике были предложены три задачи: одна по алгебре, одна по геометрии, одна по тригонометрии. Из 1000 абитуриентов задачу по алгебре решили A, по геометрии – B, по тригонометрии – C. При этом задачи по алгебре и геометрии решили D абитуриентов, по алгебре и тригонометрии – E, по геометрии и тригонометрии – F, а G абитуриентов решили все задачи. Сколько абитуриентов не решили ни одной задачи? Если:
1) A =800, B =700, C =600, D =600, E =500, F =400, G =300;
2) A =300, B =400, C =300, D =150, E =100, F =100, G =50;
3) A =450, B =500, C =450, D =100, E =200, F =250, G =50;
4) A =450, B =550, C =350, D =350, E =150, F =250, G =100;
5) A =400, B =500, C =500, D =300, E =200, F =300, G =200;
6) A =500, B =400, C =600, D =300, E =200, F =300, G =200.
Из 100 опрошенных студентов 24 не изучают ни английский, ни немецкий, ни французский языки, A изучают английский, B – английский и немецкий, C – французский, D – французский и английский, E – французский и немецкий, F – немецкий. Сколько студентов среди опрошенных изучают английский, немецкий и французский языки? Если:
7) A =36, B =11, C =41, D =21, E =11, F =36;
8) A =60, B =40, C =41, D =30, E =25, F =50;
9) A =21, B =10, C =45, D =10, E =30, F =55;
10) A =41, B =15, C =26, D =11, E =15, F =45;
11) A =55, B =30, C =35, D =20, E =20, F =41;
12) A =48, B =8, C =26, D =8, E =13, F =28.
Предположим, что, согласно исследованию, из 200 людей, смотрящих телевизор, A человек смотрят спортивную передачу, B – комедии, C предпочитают драмы, D смотрят драмы и спорт, E – комедии и спорт, F смотрят комедии и драмы и G человек смотрят все три вида передач. Сколько человек: а) смотрят спорт, комедии или драмы? б) не смотрят ничего из вышеперечисленного? Если:
13) A =110, B =120, C =85, D =50, E =70, F =55, G =30;
14) A =70, B =120, C =120, D =40, E =50, F =75, G =25;
15) A =110, B =75, C =125, D =90, E =50, F =60, G =40;
16) A =100, B =125, C =110, D =30, E =50, F =80, G =10;
17) A =110, B =75, C =130, D =95, E =50, F =65, G =45;
18) A =105, B =80, C =100, D =60, E =50, F =20, G =10.
Предположим, что из 100 опрошенных студентов A изучают химию, B –математику, C – физику, D – химию и физику, E занимаются физикой и математикой, F – математикой и химией и 5 изучают все три предмета. Сколько студентов: а) изучают хотя бы один из трех перечисленных предметов? б) не изучают ни один из трех перечисленных предметов?
в) изучают только математику? г) изучают физику или химию, но не изучают математику? д) не изучают ни математику, ни химию? Если:
19) A =50, B =53, C =42, D =15, E =20, F =25;
20) A =45, B =35, C =65, D =35, E =25, F =5;
21) A =40, B =35, C =55, D =25, E =15, F =5;
22) A =65, B =30, C =45, D =35, E =5, F =15;
23) A =40, B =45, C =55, D =25, E =20, F =10;
24) A =70, B =45, C =35, D =25, E =5, F =35.
Согласно опросу 250 телезрителей, A из них нравится смотреть новости, B предпочитают смотреть спорт, C – комедии, D – новости и комедии, E – спорт и комедии, F – новости и спорт, 5 любят все три вида программ. Сколько телезрителей: а) смотрят новости, но не смотрят спорт? б) смотрят новости или спорт, но не любят комедии? в) не любят смотреть ни новости, ни спорт?
г) смотрят все кроме спорта? д) смотрят спорт и комедии, но не смотрят новости? Если:
25) A =95, B =125, C =125, D =25, E =45, F =35;
26) A =110, B =95, C =85, D =30, E =30, F =25;
27) A =65, B =115, C =115, D =15, E =45, F =35;
28) A =100, B =90, C =110, D =30, E =25, F =30;
29) A =75, B =85, C =120, D =45, E =35, F =15;
30) A =95, B =85, C =110, D =25, E =30, F =30.
Векторы
2.1.Даны координаты векторов 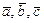 ,
,  в правом ортонормированном базисе
в правом ортонормированном базисе  . Показать, что векторы
. Показать, что векторы 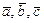 тоже образуют базис и найти координаты вектора
тоже образуют базис и найти координаты вектора  в базисе
в базисе 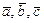 .
.
1)  , ,
|  , ,
| 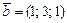 , ,
|  ; ;
|
2)  , ,
|  , ,
|  , ,
| 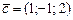 ; ;
|
3)  , ,
|  , ,
|  , ,
|  ; ;
|
4)  , ,
|  , ,
|  , ,
|  ; ;
|
5)  , ,
|  , ,
|  , ,
|  ; ;
|
6)  , ,
| 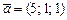 , ,
| 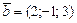 , ,
|  ; ;
|
7)  , ,
|  , ,
| 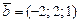 , ,
|  ; ;
|
8)  , ,
|  , ,
| 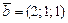 , ,
|  ; ;
|
9)  , ,
| 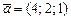 , ,
|  , ,
|  ; ;
|
10) 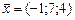 , ,
| 
|  , ,
|  ; ;
|
11)  , ,
| 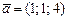 , ,
|  , ,
|  ; ;
|
12)  , ,
|  , ,
|  , ,
|  ; ;
|
13)  , ,
|  , ,
|  , ,
|  ; ;
|
14)  , ,
|  , ,
| 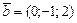 , ,
|  ; ;
|
15) 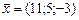 , ,
|  , ,
|  , ,
|  ; ;
|
16)  , ,
|  , ,
|  , ,
| 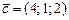 ; ;
|
17)  , ,
| 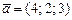 , ,
|  , ,
| 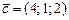 ; ;
|
18) 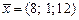 , ,
|  , ,
|  , ,
|  ; ;
|
19 
|  , ,
|  , ,
| 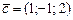 ; ;
|
20 
|  , ,
|  , ,
| 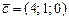 ; ;
|
21)  , ,
| 
|  , ,
|  ; ;
|
22)  , ,
|  , ,
|  , ,
|  ; ;
|
23)  , ,
|  , ,
| 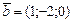 , ,
|  ; ;
|
24)  , ,
| 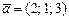 , ,
|  , ,
|  ; ;
|
25) 
|  , ,
|  , ,
| 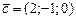 ; ;
|
26) 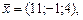
|  , ,
| 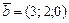 , ,
|  ; ;
|
27) 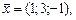
|  , ,
|  , ,
|  ; ;
|
28) 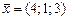 , ,
| 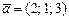 , ,
|  , ,
|  ; ;
|
29)  , ,
| 
| 
|  ; ;
|
30)  , ,
|  , ,
| 
| 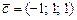 . .
|
2.2. Даны координаты точек A, B, C, D в правой прямоугольной системе координат. Вычислить с точностью 0,001:
а) скалярное произведение вектора 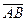 на вектор
на вектор  ;
;
б) площадь треугольника ABC;
в) объем тетраэдра ABCD.
1)  , ,
|  , ,
|  , ,
| 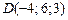 ; ;
|
2)  , ,
|  , ,
|  , ,
|  ; ;
|
3)  , ,
| 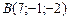 , ,
|  , ,
|  ; ;
|
4)  , ,
|  , ,
|  , ,
|  ; ;
|
5)  , ,
|  , ,
|  , ,
|  ; ;
|
6)  , ,
| 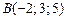 , ,
| 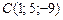 , ,
|  ; ;
|
7) 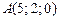 , ,
|  , ,
| 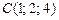 , ,
|  ; ;
|
8) 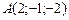 , ,
|  , ,
| 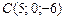 , ,
| 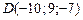 ; ;
|
9)  , ,
| 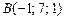 , ,
|  , ,
|  ; ;
|
10)  , ,
|  , ,
|  , ,
|  ; ;
|
11)  , ,
|  , ,
|  , ,
|  ; ;
|
12)  , ,
|  , ,
|  , ,
| 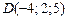 ; ;
|
13) 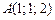 , ,
|  , ,
|  , ,
| 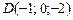 ; ;
|
14)  , ,
|  , ,
|  , ,
|  ; ;
|
15)  , ,
|  , ,
|  , ,
|  ; ;
|
16)  , ,
| 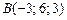 , ,
|  , ,
| 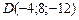 ; ;
|
17)  , ,
|  , ,
| 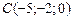 , ,
|  ; ;
|
18)  , ,
|  , ,
|  , ,
|  ; ;
|
19)  , ,
|  , ,
|  , ,
|  ; ;
|
20)  , ,
|  , ,
|  , ,
|  ; ;
|
21)  , ,
|  , ,
|  , ,
| 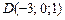 ; ;
|
22) 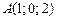 , ,
|  , ,
|  , ,
|  ; ;
|
23)  , ,
| 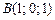 , ,
|  , ,
|  ; ;
|
24)  , ,
|  , ,
|  , ,
|  ; ;
|
25)  , ,
|  , ,
|  , ,
| 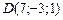 ; ;
|
26) 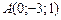 , ,
|  , ,
|  , ,
|  ; ;
|
27)  , ,
|  , ,
| 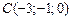 , ,
|  ; ;
|
28)  , ,
|  , ,
|  , ,
| 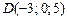 ; ;
|
29) 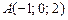 , ,
| 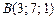 , ,
|  , ,
| 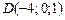 ; ;
|
30) 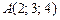
|  , ,
|  , ,
| 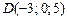 . .
|
Прямая на плоскости
3.1. Даны уравнения двух прямых. Показать, что один из образованных ими смежных углов – острый, и найти уравнение биссектрисы этого угла. Сделать чертеж.
1) 3 x –4 y –2=0, 8 x –6 y +15=0; 2) 2 x +3 y +9=0, 3 x +2 y –10=0; 3) 5 x –12 y –24=0, 5 x +12 y –4=0; 4) 2 x + y +5=0, x +2 y +9=0; 5) 3 x –2 y +10=0, 3 x +2 y +9=0; 6) x –7 y +5=0, 5 x +5 y +3=0; 7) 7 x + y =0, x + y =0; 8) 2 x –3 y –5=0, 6 x –4 y +7=0; 9) x –3 y +5=0, 3 x – y +8=0;
10) 3 x +4 y +2=0, 8 x +6 y -15=0; 11) 2 x –3 y –9=0, 3 x –2 y +10=0; 12) 5 x +12 y +24=0, 5 x –12 y +4=0; 13) 2 x – y –5=0, x –2 y –6=0; 14) 3 x +2 y –10=0, 3 x –2 y –9=0; 15) x +7 y –5=0, 5 x –5 y –3=0; 16) 2 x +3 y +5=0, 6 x +4 y –7=0; 17) x +3 y –5=0, 3 x + y –8=0;
Даны координаты вершин A и B треугольника ABC и точки M пересечения его высот. Найти координаты вершины C. Сделать чертеж.
18) A (–10;2), B (6;4), M (5;2); 19) A (–6;2), B (2;–2), M (1;2); 20) A (3;–1), B (5;7), M (4;–1); 21) A (2;6), B (3;–1), M (–1;2); 22) A (–2;1), B (2;5), M (0,5;0,5);
23) A (5;2), B (5; -2), M (17/6;20/3); 24) A (3;2), B (2;3), M (– 7;– 13);
25) A (9;–3), B (–5;–5), M (0;0); 26) A (–1;3), B (7;5), M (–1;4);
27) A (10;–2), B (–6;–4), M (–5;–2); 28) A (6;–2), B (–2;2), M (–1;–2);
29) A (–3;1), B (– 5;– 7), M (– 4;1); 30) A (– 2;– 6), B (– 3;1), M (1;– 2).
3.2. Даны координаты вершин треугольника ABC. Найти уравнение стороны BC, а также уравнения биссектрисы, медианы и высоты, проведенных из вершины A. Все уравнения прямых дать в канонической форме.
1) A (1; 1), B (4; –3), С (7; 9); 2) A (1; 1), B (5; –2), С (7; 9); 3) A (1; 3), B (4; 7), С (5; 0);
4) A (0; –1), B (–6; –9), С (–4; 2); 5) A (6; –1), B (9; 3), С (–2; 5); 6) A (4; –1), B (7; –5), С (10; 7);
7) A (1; 2), B (–5; –6), С (–3; 5);8) A (–1; 2), B (3; –1), С (–9; –4); 9) A (3; –1), B (7; –4), С (6; 3);
10) A (1; –1), B (–5; –9), С (–3; 2); 11) A (3; 8), B (7; 5), С (–5; 2); 12) A (2; 1), B (–1; 5), С (10; 7);
13) A (–1; 1), B (–7; –7), С (–5; 4); 14) A (1; 3), B (5; 0), С (–7; –3); 15) A (3; 2), B (0; 6), С (11; 8);
16) A (1; –1), B (4; 3), С (–7; 5); 17) A (4; –2), B (8; –5), С (–4; –8); 18) A (4; 1), B (1; 5), С (12; 7);
19) A (–1; 1), B (2; 3), С (–9; 5); 20) A (1; –2), B (4; –6), С (7; 6); 21) A (6; 2), B (3; 6), С (14; 8);
22) A (–3; 2), B (0; 6), С (–12; 8); 23) A (6; 1), B (9; –3), С (12; 9); 24) A (1; 5), B (5; 2), С (4; 9);
25) A (–1;–1), B (–4;–3), С (–7; 9); 26) A (–6; 1), B (–9;–3), С (2;–5); 27) A (–4; 1), B (–7; 5), С (–10;–7);
28) A (–1;–2), B (5; 6), С (3;–5); 29) A (–3;–8), B (–7;–5), С (5;–2); 30) A (–2;–1), B (1;–5), С (–10;–7).
Плоскость и прямая в пространстве
4.1. Даны координаты точки M и уравнение плоскости. Найти координаты точки, симметричной точке M относительно плоскости.
1) M (1;0;1), 4 x +6 y +4 z –25=0; 2) M (–1;0;–1), 2 x +6 y –2 z +11=0; 3) M (0;2;1), 2 x +4 y –3=0; 4) M (2;1;0), y + z +2=0; 5) M (–1;2;0), 4 x –5 y – z –7=0; 6) M (2;–1;1), x – y +2 z –2=0; 7) M (1; 1; 1), x +4 y +3 z +5=0; 8) M (1;2;3), 2 x +10 y +10 z –1=0; 9) M (0;–3;–2), 2 x +10 y +10 z –1=0; 10) M (1;0;–1), 2 y +4 z –1=0; 11) M (3;–3;–1), 2 x –4 y –4 z –13=0; 12) M (–2;–3;0), x +5 y +4=0; 13) M (2;–2;–3), y + z +2=0; 14) M (–1;0;1), 2 x +4 y –3=0; 15) M (3;3;3), 8 x +6 y +8 z –25=0;
16) M (–2;0;3), 2 x –2 y +10 z +1=0.
Даны координаты точки M и уравнения прямой. Найти координаты точки, симметричной точке M относительно прямой.
17) M (0;–3;–2),  ; 18) M (2;–1; 1),
; 18) M (2;–1; 1),  ;
;
19) M (1;1;1),  ; 20) M (1;2;3),
; 20) M (1;2;3),  ;
;
21) M (1; 0;–1),  ; 22) M (2; 1; 0),
; 22) M (2; 1; 0), 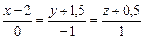 ;
;
23) M (–2;–3; 0),  ; 24) M (–1; 0;–1),
; 24) M (–1; 0;–1),  ;
;
25) M (0; 2; 1),  ; 26) M (3;–3;–1),
; 26) M (3;–3;–1),  ;
;
27) M (0; 3; 2),  ; 28) M (0; 2;–1),
; 28) M (0; 2;–1), 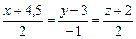 ;
;
29) M (–1;–1;–1),  ; 30) M (2;3;0),
; 30) M (2;3;0),  .
.
4.2. Даны уравнения двух прямых в пространстве. Если прямые параллельны или пересекаются, то написать уравнение содержащей их плоскости. Если прямые скрещиваются, то написать уравнение плоскости, содержащей первую прямую и параллельной одной из прямых, содержащей другую прямую.
1) 
 ;
;
2) 
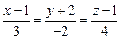 ;
;
3) 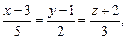
 ;
;
4) 
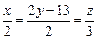 ;
;
5) 
 ;
;
6) 
 ;
;
7) 
 ;
;
8) 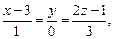
 ;
;
9) 
 ;
;
10) 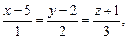
 ;
;
11) 
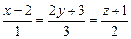 ;
;
12) 
 ;
;
13) 
 ;
;
14) 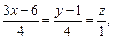
 ;
;
15) 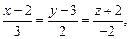
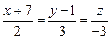 ;
;
16) 
 ;
;
17) 
 ;
;
18) 
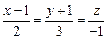 ;
;
19) 
 ;
;
20) 
 ;
;
21) 
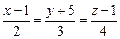 ;
;
22) 
 ;
;
23) 
 ;
;
24) 
 ;
;
25) 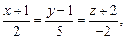
 ;
;
26) 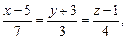
 ;
;
27) 
 ;
;
28) 
 ;
;
29) 
 ;
;
30) 
 .
.
4.3. Найти расстояние между двумя прямыми.
1) 

2) 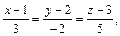
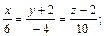
3) 

4) 
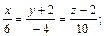
5) 

6) 

7) 

8) 

9) 

10) 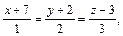

11) 
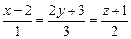 ;
;
12) 
 ;
;
13) 
 ;
;
14) 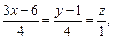
 ;
;
15) 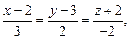
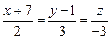 ;
;
16) 
 ;
;
17) 
 ;
;
18) 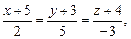
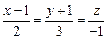 ;
;
19) 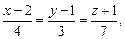
 ;
;
20) 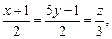
 ;
;
21) 
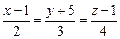 ;
;
22) 
 ;
;
23) 
 ;
;
24) 
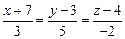 ;
;
25) 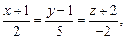
 ;
;
26) 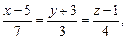
 ;
;
27) 
 ;
; 
28) 
 ;
;
29) 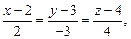
 ;
;
30) 
 .
.
Определители
5.1. Вычислить определители:
1)  2)
2) 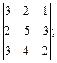 3)
3)  4)
4) 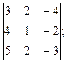 5)
5)  6)
6)  7)
7)  8)
8)  9)
9)  10)
10) 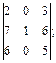 11)
11)  12)
12) 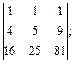 13)
13)  14)
14) 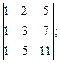 15)
15) 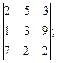 16)
16)  17)
17)  18)
18) 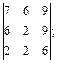 19)
19) 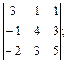 20)
20)  21)
21)  22)
22)  23)
23) 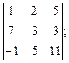 24)
24) 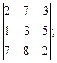 25)
25) 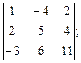 26)
26)  27)
27)  28)
28)  29)
29)  30)
30) 
5.2. Вычислить определители: а) разложением по строке или столбцу; б) приведением к треугольному виду.
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6) 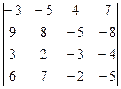 ; 7)
; 7)  ; 8)
; 8) 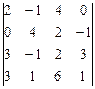 ; 9)
; 9)  ; 10)
; 10) 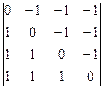 ; 11)
; 11)  ; 12)
; 12) 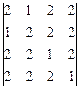 ; 13)
; 13)  ; 14)
; 14)  ; 15)
; 15) 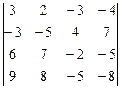 ; 16)
; 16)  ; 17)
; 17)  ; 18)
; 18)  ; 19)
; 19) 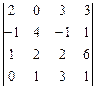 ; 20)
; 20)  ; 21)
; 21)  ; 22)
; 22)  ; 23)
; 23)  ; 24)
; 24)  ; 25)
; 25)  ; 26)
; 26)  ; 27)
; 27)  ; 28)
; 28)  ; 29)
; 29)  ; 30)
; 30) 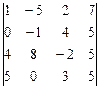 .
.
5.3.Выяснить, какие из приведенных ниже произведений входят в определитель и с каким знаком.
1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6)  7)
7)  8)
8) 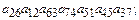 9)
9) 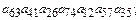 10)
10)  11)
11)  12)
12)  13)
13)  14)
14) 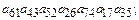 15)
15)  16)
16)  17)
17)  18)
18)  19)
19)  20)
20)  21)
21)  22)
22)  23)
23) 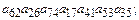 24)
24)  25)
25) 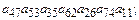 26)
26)  27)
27) 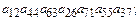 28)
28)  29)
29) 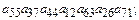 30)
30) 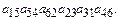
Матрицы
6.1. Найти  и
и  если:
если:
1)  2)
2) 

3) 

 4)
4) 


5) 

 6)
6) 


7) 

 8) A=
8) A= 

9) 
 10)
10) 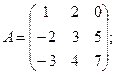

11) 
 12 )
12 )  13)
13)  14)
14)