Ответ:
Волновое сопротивление возникает от того, что судно при движении по воде образует на ее поверхности волны. Затрата энергии на их образование определяет величину волнового сопротивления. С увеличением скорости волновое сопротивление растет, причем быстрее, чем сопротивление трения.
Этим и объясняется меньшая доля сопротивления трения при больших скоростях движения.
Волновое сопротивление, кроме того, зависит от длины судна и его водоизмещения, а также от формы корпуса (как говорят, обводов), в частности от его полноты. Чем больше длина судна, тем меньше, при прочих равных условиях, волновое сопротивление.
Точнее говоря, волновое сопротивление существенно зависит не от самой длины яхты, а от ее относительной скорости, которую определяют отношением скорости к квадратному корню из длины по ватерлинии. Опыты показывают, что волновое сопротивление практически отсутствует при относительной скорости *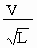 
- меньше 0,4—0,45 и начинает интенсивно расти при - 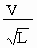- больше 0,9.
При больших скоростях волновое сопротивление увеличивается так сильно, что прирост скорости водоизмещающей яхты становится малозаметным даже при значительном усилении ветра или увеличении площади парусности. Обычным во-доизмещающим яхтам практически трудно достичь скорости большей, чем (1,45—1,5)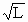 
. При этой скорости волновое сопротивление составляет уже 60—70% общего сопротивления.
Характеристикой волнового сопротивления судна является отношение скорости к длине, называемое числом Фруда:
Fr = v / √gL
Эта характеристика позволяет сравнивать суда различных размеров, что дает возможность определить сопротивление и тем самым мощность двигателя для строящегося судна с помощью буксировочных испытаний моделей. Скорости судна и модели соотносятся как квадратные корни из их линейных размерений:
| v судна | = | v модели | = Fr |
| −−−−−−−− | −−−−−−−−− | ||
| √gL судна | √gL модели |
Это означает, например, что строящемуся судну длиной 130 м, шириной 14 м с осадкой 6,6 м, с водоизмещением 5900 т и скоростью 25 уз (12,86 м/с) соответствует скорость модели 2,572 м/с при длине ее 5,2 м. При этой скорости у модели возникает волнообразование, которое геометрически подобно волнообразованию натурного судна. Измеренное при этом сопротивление содержит, однако, не только волновое сопротивление, но и еще один компонент - сопротивление трения, которое возникает вследствие тормозящего действия воды, протекающей мимо корпуса. Сопротивление трения зависит от площади смоченной поверхности корпуса, от ее качества (степени шероховатости) и от скорости. Его можно рассчитать с достаточной точностью по опытным данным как для модели, так и для судна. Если полное сопротивление модели уменьшить на расчетный коэффициент трения, получится волновое сопротивление модели. При пересчете действует положение, что волновые сопротивления двух геометрических подобных тел - судна и модели - соотносятся как их водоизмещения. Но это простое соотношение справедливо только тогда, когда судно и модель движутся со сравнимыми скоростями, так что возникают геометрически подобные волнообразования. Если к волновому сопротивлению (определенному опытами на модели) прибавить расчетное сопротивление трения, получится полное сопротивление судна. В нашем примере при модельных испытаниях было определено волновое сопротивление в 0,31 МН и путем расчета - сопротивление трения в 0,35 МН. Полное сопротивление судна составляет, таким образом, 0,66 МН. Разумеется, при окончательном определении потребной мощности двигателей нужно учитывать также воздушное и вихревое сопротивления.
Доля волнового сопротивления и сопротивления трения в полном сопротивлении зависит от формы судна и его скорости. У больших тихоходных судов волновое сопротивление составляет примерно 20%, а у очень быстроходных - до 70% полного сопротивления.