Двигатели постоянного тока различаются по характеру возбуждения. Двигатели могут быть независимого, параллельного, последовательного и смешанного возбуждения (см.  ). Свойства двигателей в значительной мере определяются их системой возбуждения.
). Свойства двигателей в значительной мере определяются их системой возбуждения.

Рис. 5-5а,б,в,г. Возбуждение ДПТ.
Поскольку в автоматике применяются в основном двигатели независимого возбуждения, будем в дальнейшем рассматривать двигатели этого типа ( ).
).
Различают статические и динамические режимы работы двигателей. В статическом режиме ω=const; IЯ=const; UДВ=const и он описывается так называемыми механическими характеристиками
 .
.
В статическом режиме двигатель независимого возбуждения описывается следующей системой уравнений:


где первое уравнение - уравнение якорной цепи, второе и третье -  и
и  , четвертое - механическое уравнение, пятое - уравнение цепи возбуждения.
, четвертое - механическое уравнение, пятое - уравнение цепи возбуждения.
Из первых четырех уравнений  получим уравнение механической характеристики:
получим уравнение механической характеристики:
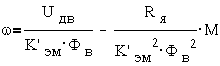

Поскольку применяемые в системах автоматического управления двигатели являются управляемыми, различают два типа управления двигателями постоянного тока - якорное управление и полюсное управление.
При якорном управлении производится изменение напряжения, подаваемого в якорную цепь без изменения возбуждения. При полюсном управлении, наоборот, меняется поле возбуждения путем изменения тока в обмотках главных полюсов iB. Для расширения диапазона управления применяют также комбинированное управление.
При полюсном управлении ФB=const, поэтому уравнение механической характеристики согласно  будет иметь вид:
будет иметь вид:


Графически эта характеристика при фиксированном напряжении на двигателе представляет собой прямую, пересекающую координатные оси в точках ω0 и MК.З. (см.  ), где ω0- частота вращения холостого хода, а MК.З.- момент короткого замыкания, когда ротор двигателя неподвижен.
), где ω0- частота вращения холостого хода, а MК.З.- момент короткого замыкания, когда ротор двигателя неподвижен.

Рис. 5-6а. Статическая характеристика ДПТ.
Электрическая машина работает в режиме двигателя при 0<M<MК.З., при M>MК.З. происходит вращение двигателя в противоположную сторону под действием внешнего момента - машина работает в режиме тормоза (режим противовключения), при ω>ω0 машина работает в режиме генератора на сеть, имеющую напряжение UH.
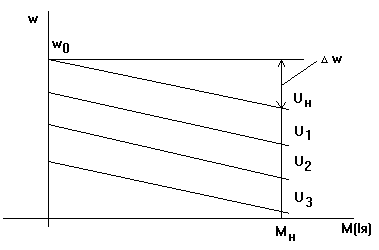
Рис. 5-6б. Статическая характеристика ДПТ.
Механические характеристики при различных напряжениях питания двигателя выглядят, как семейство прямых, показанных на  . Часто их строят в функции тока якоря IЯ, тогда аналитическое выражение для механических характеристик примет вид:
. Часто их строят в функции тока якоря IЯ, тогда аналитическое выражение для механических характеристик примет вид:

 ,
,
откуда видно, что падение скорости при нагрузке двигателя зависит исключительно от сопротивления якорной цепи RЯ.
Кроме механических, существуют регулировочные характеристики. Для якорного управления это зависимость частоты вращения от напряжения питания UДВ. Вид этих характеристик показан на  , где UТР- напряжение трогания двигателя.
, где UТР- напряжение трогания двигателя.
Регулировочная характеристика для полюсного управления может быть получена из  при UДВ=const.
при UДВ=const.

Рис. 5-6в. Статическая характеристика ДПТ.
Вид этих характеристик при различных нагрузках показан на  .
.

Рис. 5-6г. Статическая характеристика ДПТ.
Для холостого хода, когда M=0, эта характеристика имеет вид гиперболы

Двигатель постоянного тока как динамическая система описывается следующими уравнениями в операторной форме:


На основании этих уравнений может быть построена структурная схема двигателя как динамической системы ( ).
).

Рис. 5-7а. Структурная схема ДПТ.
Из структурной схему получим передаточные функции двигателя:




где  - коэффициент передачи,
- коэффициент передачи,  - постоянная времени якоря,
- постоянная времени якоря,  - электромеханическая постоянная времени.
- электромеханическая постоянная времени.
Пользуясь формулой Хевисайда, по передаточным функциям можно построить переходные процессы, например при пуске двигателя, как это показано на  .
.
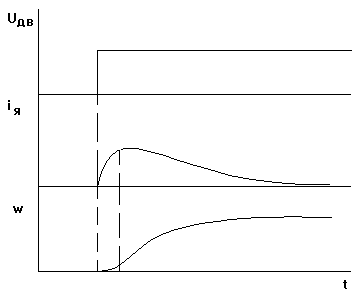
Рис. 5-7б. Переходный процесс при пуске ДПТ.
При TM»TЯ, как это обычно бывает, получим выражения для тока и скорости при пуске:


Для анализа динамики двигателя постоянного тока при полюсном управлении рассматривают уравнения, аналогичные уравнениям  в отклонениях, так как регулировочная характеристика при полюсном управлении является нелинейной.
в отклонениях, так как регулировочная характеристика при полюсном управлении является нелинейной.
Производят линеаризацию системы для малых отклонений относительно каких-то нулевых значений, представив переменные в следующем виде:
 ;
;  ;
; 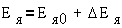 ;
;  ;
; 
Тогда на основании уравнений  можно написать уравнения в отклонениях (при TЯ=0).
можно написать уравнения в отклонениях (при TЯ=0).


На основании этих уравнений может быть построена структурная схема двигателя как динамической системы при полюсном управлении ( ).
).

Рис. 5-8а. Структурная схема ДПТ при полюсном управлении.
С помощью этой схемы получим передаточную функцию для ДПТ при полюсном управлении


По этой передаточной функции, пользуясь формулой Хевисайда, можно получить кривые переходного процесса в двигателе при ступенчатом изменении напряжения возбуждения, показанные на  .
.

Рис. 5-8б. Переходный процесс при пуске ДПТ при полюсном управлении.