например: ХИ2ОБР(0.05; 5).
Сравниваем χ2 и χ2крит, если χ2 < χ2крит, то гипотезу H0 о совпадении фактического распределения с теоретическим принимаем.
Практически mi должны быть больше или равны 5, если в некотором интервале это условие нарушается, то интервал объединяется с соседним.
ПРИМЕР 1.
В результате 300 бросков кости (кубика с 6 гранями) были получены следующие результаты (табл.1):
Таблица 1
| Кол-во очков | ||||||
| Кол-во повторений |
Проверить гипотезу о том, что кость «правильная».
Решение.
Если кость «правильная», то все значения в таблице должны встречаться более–менее одинаково. Такую картину имеет равномерный закон распределения, при котором каждый из шести возможных исходов (кол-во выпавших очков) равновероятен, т.е. Pi =1/6 для всех i =1,2…6. Таким образом, задача гипотезы о «правильности» кости сводиться к проверке гипотезы H0 о том, что выборка приведенная в табл. 1 является равномерно распределенной. Альтернативной является гипотеза H1 – данная выборка не является равномерно распределенной. Все расчеты сведем в табл. 2.
Таблица 2
| Xi | mi | Pi | N*Pi | (mi-N*Pi)^2 /N*Pi | |
| 0,1667 | 2,88 | ||||
| 0,1667 | 2,88 | ||||
| 0,1667 | 0,00 | ||||
| 0,1667 | 0,08 | ||||
| 0,1667 | 0,98 | ||||
| 0,1667 | 4,50 | ||||
| N= | 11,32 | Xi-квадрат |
Получено значение χ2 =11.320. В нашем случае r = 6-1= 5 и при α =0.05, находим χ2крит = 11.07. Поэтому гипотеза H0 о равномерном распределении отвергается, и принимается альтернативная гипотеза H1 . Приходим к выводу, что кость «неправильная».
ПРИМЕР 2
Проверить гипотезу о том, что распределение, представленное в таблице 3. является частным случаем нормального распределения (уровень значимости α =0,05). (См. материалы лабораторной работы №3, табл.3.1.)
Таблица3.
| Интервал | [-4;-2] | [-2;0] | [0;2] | [2;4] | [4;6] | [6;8] | [8;10] | [10;12] | [12;14] |
| Частота mi |
Решение.
Построим полигон распределения (рис. 4.1 б, кривая синего цвета). Кривая имеет колокообразную форму и симметрична, поэтому можно сделать предположение, что генеральная совокупность распределена по нормальному закону. Выдвигаем гипотезу Но: данное распределение нормально. Альтернативная гипотеза – Н1: распределение не является нормальным.
Воспользуемся результатами, полученными в лаб.раб. 3. Будем считать, что диапазон ячеек C67:N81 уже заполнен, т.е. уже вычислено среднее значение 
равное 4.77 и стандартное отклонение s равное 3.03.
· интервале ячеек D70:E78 записаны значения левой и правой границ интервала;
· в интервале ячеек F70:F78 – середины интервалов;
· в интервале ячеек G70:G78 - наблюдаемые значения частоты mi.
Как уже упоминалось ранее (лаб.раб 2), случайная величина называется распределенной по нормальному (Гауссовскому) закону, если она имеет следующую плотность распределения
(4.3).
Величина m и σ – параметр распределения. Известно, что математического ожидание такой случайной величины равно m, дисперсия - σ2 (стандартное отклонение σ). Это существенно используется при проверке гипотезы.
Рис. 4.1 а
Сначала определяем значение m. Поскольку оно имеет смысл математического ожидания, то в качестве m возьмем xср =4.77. Именно это значение будем использовать для построения теоретического распределения.
Далее определяем параметр σ, в качестве этого значения возьмем 3.04 - это и есть оценка значения σ. Это значение будем использовать для построения теоретического распределения.
Наша следующая подзадача - вычислить pi - теоретические значения вероятности того, что случайная величина, имеющая нормальное распределение с параметрами a =4,77 и σ =3,04 попадает в i-ый интервал.
Для этого воспользуемся соотношениями:
(4.6)
(4.7)
где F(x) – функция распределения. В MS Excel для нормального закона распределения с параметрами a и σ значение F(x) можно вычислить, воспользовавшись встроенной функцией НОРМРАСП:
F(x) =НОРМРАСП(x; a; σ; ИСТИНА).
Выполняем:
В ячейки N70:N78 заносим значения F(bi);
В ячейки M70:M78 заносим значения F(ai);
В интервале O70:O78 получаем теоретические значения вероятности, вычисленные по формуле (4.7) (F(bi)- F(ai)).
В интервал P70:P78 заносим теоретические значения частот, вычисленные по формуле 
.
Для визуального сравнения наблюдаемых mi и теоретических частот построим соответствующие графики – полигоны частот, по оси ординат отложим середины интервалов (красная кривая для теоретических частот) (рис.4.1 б). Анализируя эти графики, заметим, что распределения по тенденциям схожи: симметричность относительно оси проходящей через максимум и плавное убывание по мере удаления от максимума.
Рис. 4.1 б
Заметим, что в некоторых интервалах значения теоретических частот получились меньше 5, объединим эти интервалы. Таких интервалов у нас 6:1,2,3,7,8 и 9. Объединим интервалы с 1 по 3 включительно, соответствующие значения наблюдаемых и теоретических частот просто суммируются, заполнив ячейки Q72 и R72.
Объединим интервалы с 7 по 9 включительно, соответствующие значения наблюдаемых и теоретических частот просто суммируются, заполнив ячейки Q76 и R76.
Ячейки Q73:R75 заполняются очевидным образом.
После этого объединения число интервалов у нас сократилось до 5, т.е. теперь k=5.
Теперь мы готовы вычислить χ2 по формуле (4.1). Для этого в ячейку S72 заносим формулу =(Q72-R72)^2/R72, в остальные ячейки диапазона S72:S76 формула заносится копированием. Сумму значений ячеек S72:S76 помещаем в ячейку S79 – это искомое значение χ2. = 3,04.
Определим число степеней свободы r по формуле (4.2). Поскольку k =5, c=2, то r = 2. Для α = 0,05 и r = 2 найдем χ2крит, используя встроенную функцию EXCEL =ХИ2ОБР(0.05;2). χ2крит = 5.99
Поскольку χ2 < χ2крит, то гипотезу H0 о соответствии случайной величины x нормальному закону распределения принимаем (Согласно выборочным экспериментальным данным нет оснований отвергнуть гипотезу Но).
Критерий Фишера
F - критерий Фишера используют для сравнения дисперсий двух вариационных рядов.
Выдвигается гипотеза H0, что дисперсии выборок равны, альтернативная гипотеза H1 - они не равны. Вычисляется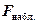 
по формуле:
, (4.8)
где 
- большая дисперсия, 
- меньшая дисперсия. По трем величинам - уровень значимости, число степеней свободы числителя и число степеней свободы знаменателя - определяем 
по таблицам или используя встроенные функции Excel.
Число степеней свободы числителя определяется по формуле:
, (4.9)
где n1 - число вариант для большей дисперсии.
Число степеней свободы знаменателя определяется по формуле:
, (4.10)
где n2 - число вариант для меньшей дисперсии.
Если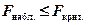 
(вычисленное значение критерия 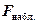не больше критического), то принимается гипотеза H0 (дисперсии равны), в противоположном случае (
) принимается гипотеза H1 (дисперсии различны).
ПРИМЕР 3
При проведении тестирования двух одинаковых приборов были проведены измерения эталона. При этом первым прибором были проведены n1 =11 измерений, а вторым n2 =9. Результаты были записаны в виде отклонений от величины эталона. Требуется выяснить: одинаковой ли точностью обладают приборы?
Решение:
Рис. 4.2
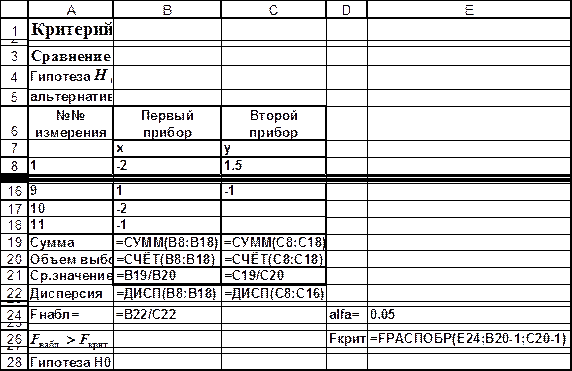
Рис. 4.3.
При измерении величины отклонений для первого прибора (n1 =11) результаты внесены в столбец В, а для второго прибора (n2 =9) результаты внесены в столбец С. (рис. 4.2) Подсчет средних показал, что они одинаковы и равны нулю. Следовательно, у приборов отсутствует систематическая ошибка.
Проверка точности приборов сводится к проверке совпадения дисперсий. Если дисперсии статистически равны, то приборы обладают одинаковой точностью. Выдвигается гипотеза H0, что дисперсии выборок равны, альтернативная гипотеза H1 - они не равны.
В результате расчета были получены соответственно следующие величины дисперсий - =7.35 и =2.188. Значение критерия 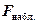=7.35 /2.188 составило 3.36. По уровню значимости α=0.05; числу степеней свободы числителя r1 =11-1=10 и числу степеней свободы знаменателя r2 =9-1=8 находим Fкрит =3,347. Fкрит найдено используявстроенную функцию FРАСПОБР(). Поскольку 
то гипотеза H0 отклоняется, а принимается альтернативная гипотеза H1 (дисперсии различны). Следовательно, приборы имеют различную точность.
Cредство анализа надстройки «Пакет анализа» MS Excel «Двухвыборочный F-тест для дисперсии». Это средство анализа служит проверки гипотезы о равенстве дисперсий двух выборок. Для проверки необходимо заполнить диалоговое окно, приведенное на рис. 4.4, назначение всех полей очевидно. Результат работы представлен на следующем рисунке. Сравните полученные результаты, с результатами, полученными вручную.
Рис. 4.4
Рис. 4.5