Cредство анализа надстройки «Пакет анализа» MS Excel «Двухвыборочный t-тест с одинаковыми дисперсиями»

Это средство анализа служит проверки гипотезы о равенстве средних двух независимых нормально распределенных выборок с одинаковыми дисперсиями. Для проверки необходимо заполнить диалоговое окно, приведенное на рис.4.8, назначение всех полей очевидно. Результат работы представлен на следующем рисунке. Сравните полученные результаты, с результатами, полученными вручную.

Рис. 4.9

Рис. 4.8

Дисперсии выборок неравны;

В этом случае

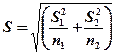(4.14)

где 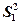и 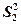- выборочные стандартные отклонения, а число степеней свободы определяется довольно сложным способом, на практике, как правило, оно вычисляется с помощью статистических пакетов или в явной форме или в неявной форме как, например, в Excel.

Cредство анализа надстройки «Пакет анализа» MS Excel «Двухвыборочный t-тест с различными дисперсиями»

Это средство анализа служит проверки гипотезы о равенстве средних двух независимых нормально распределенных выборок с различными дисперсиями. Для проверки необходимо заполнить диалоговое окно, приведенное на рис.4.10, назначение всех полей очевидно.

Рис.4.10

б) случай двух зависимых выборок

Вычисление значения 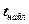осуществляется по формуле (4.11), которая в данном случае примет вид:

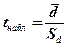(4.15)

где 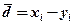— разности между соответствующими значениями переменной X и переменной У, а 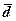- среднее этих разностей;

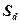вычисляется по следующей формуле:

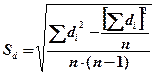(4.16)

Число степеней свободы k определяется по формуле 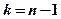. Рассмотрим пример использования t-критерия Стьюдента для связных и, очевидно, равных по численности выборок.

ПРИМЕР 5

. Изучался уровень влияния тренинга после приема традиционных лекарств на частоту сердечных сокращений (ЧСС) у группы пациентов, страдающих тахикордией. С этой целью в экспериментальной группе проводилось измерение ЧСС до и после сеанса тренинга. Требуется проверить эффективность этой методики.

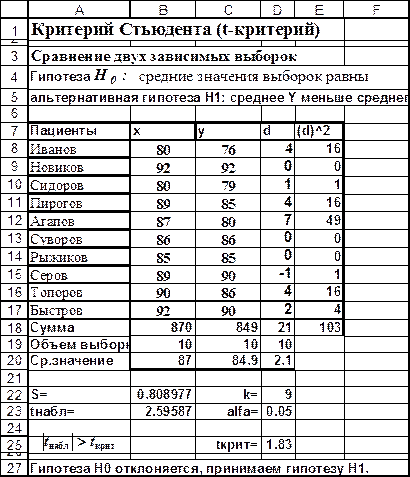
Рис. 4.11

Решение

В столбце B (рис. 4.11) содержатся значения 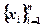ЧСС после приема лекарств без тренинга, в столбце С 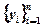ЧСС после приема лекарств после сеанса тренинга

Очевидно, что в данном примере применима методика для связных и, очевидно, равных по численности выборок. Вначале произведем расчет 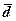(ячейка D20):

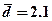
Затем применим формулу (4.16), получим:

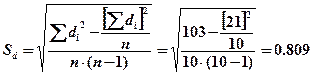
И, наконец, следует применить формулу (4.15). Получим:

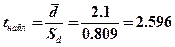
Число степеней свободы: 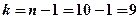и с помощью встроенной функции находим =СТЬЮДРАСПОБР(2*D23;D22). При вычислении следует учесть, что в данной задаче следует рассматривать одностороннюю критическую область. Множитель равный 2 перед уровнем значимости добавлен в силу конструктивной особенности этой функции (см.лаб.раб.2) 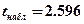, откуда следует возможность принятия альтернативной гипотезы (H₁) о достоверном уменьшении ЧСС, т. е. делается вывод об эффективности экспериментального воздействия.

В терминах статистических гипотез полученный результат будет звучать так: на 5% уровне гипотеза Н₀ отклоняется и принимается гипотеза Н₁.

Cредство анализа надстройки «Пакет анализа» MS Excel «Парный двухвыборочный t-тест для средних»

Это средство анализа служит проверки гипотезы о равенстве средних парных наблюдений, когда наблюдения собранны в пары, и нужно исследовать разницу между ними. Для проверки необходимо заполнить диалоговое окно, приведенное на рис.4.12., назначение всех полей очевидно. Результат работы представлен на следующем рисунке (рис.4.13). Сравните полученные результаты, с результатами, полученными вручную.

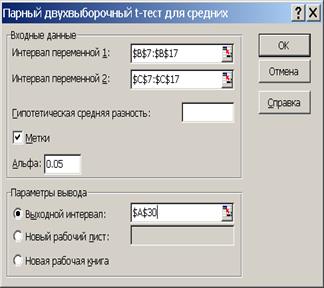
Рис. 4.12

Рис. 4.13

ЗАДАНИЕ.

Задача 1

Изучается распределение непрерывного признака Х на объектах генеральной совокупности. С этой целью из генеральной совокупности извлечена выборка объема n. Все варианты и исходные данные взять из лаб. раб.3, предполагается, что все необходимые характеристики в указанной работе уже вычислены.

Требуется:

Проверить гипотезу о нормальности экспериментального распределения.

Решение

задачи 1 приведено выше.

Задача 2

Текст задачи в зависимости от варианта приведен ниже.

Пример задачи 2

В рабочей книге MS Excel Лечебницы.xls содержится случайная выборка данных о лечебницах, собранная Отделом здравоохранения штата Нью-Мексико. Ее фрагмент приведен на рис. 4.14

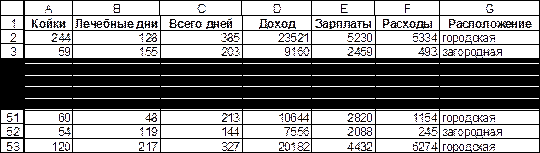
Рис. 4.14

Требуется:

Выяснить, есть ли разница между доходами городских и загородных лечебниц.

Решение

Выдвигаем гипотезу H₀: средние значения доходов городских и загородных лечебниц выборок равны, альтернативная гипотеза H₁: они не равны.

Чтобы проверить эту гипотезу по t-критерию необходимо выполнить ряд операций:

1. разделить выборку на две части: одна часть для городских, другая часть для загородных лечебниц, в дальнейшем считать эти части самостоятельными выборками;

2. выяснить, имеют ли эти выборки одинаковую дисперсию, если да, то перейти к пункту 3, иначе к пункту 4;

3. применить двухвыборочный t-тест с одинаковыми дисперсиями;

4. применить двухвыборочный t-тест с различными дисперсиями.

1. Для деления выборки воспользоваться Данные Сортировка. Результат приведен на рис. 4.15. Все данные расположенные в интервале строк 59:76 будем считать, что это элементы первой выборки, а данные в интервале строк 77:110 - это элементы второй выборки.

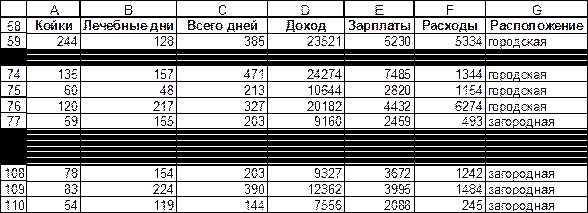
Рис. 4.15

2. Для проверки ли эти выборки одинаковую дисперсию, воспользуемся критерием Фишера.

Выдвигаем гипотезу H₀, что дисперсии выборок равны, альтернативная гипотеза H₁ - они не равны.

Воспользуемся надстройкой MS Excel «Пакет анализа» «Двухвыборочный F-тест для дисперсии», результат приведен на рис. 4.16

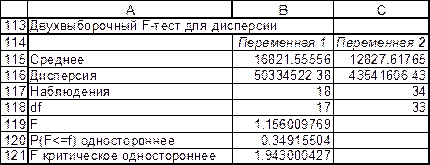
Рис. 4.16

Поскольку 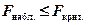(вычисленное значение критерия 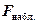не больше критического), то принимается гипотеза H₀ (дисперсии равны), Отсюда следует, что можно применить двухвыборочный t-тест с одинаковыми дисперсиями.

Выдвигаем гипотезу H₀: средние значения выборок равны, альтернативная гипотеза H₁: они не равны. Воспользуемся надстройкой MS Excel «Пакет анализа» «Двухвыборочный t-тест с одинаковыми дисперсиями», результат приведен на рис. 4.16

Рис. 4.17

В качестве следует рассматривать двухстороннее значение. Анализируя величины 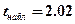и 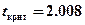, получаем , следовательно гипотеза H₀ отклоняется, H₁ - принимается. Из этого следует вывод о том, что средние значения доходов городских и загородных лечебниц различны.

Задача 2

Вариант 1

В рабочей книге MS Excel Лечебницы.xls содержится случайная выборка данных о лечебницах, собранная Отделом здравоохранения штата Нью-Мексико.

Определите, есть ли статистически значимая разница между размерами (выраженная в количестве коек) загородных и городских.

Вариант 2

Верно ли, что загородные лечебницы используются реже, чем городские (с учетом разницы в размерах лечебницы).

Указание. В качестве характеристики использования лечебницы ввести переменную «Дней_на_койку», равную отношению количеству «Лечебные дни» к значению «Койки» для загородных и городских лечебниц.

Вариант 3

Верно ли, что загородные лечебницы имеют более низкий объем заработной платы, чем городские.

Вариант 4

Верно ли, что объем расходов в загородных лечебницах ниже, чем в городских (с учетом разницы в размерах лечебницы)?

Указание. В качестве характеристики объем расходов с учетом разницы в размерах лечебницы ввести переменную «Расход_на_койку», равную отношению количеству «Расходы» к значению «Койки» для загородных и городских лечебниц.

Вариант 5

В рабочей книге MS Excel ПреподКолледж.xls содержатся данных о заработной плате преподавателей колледжа. Верно ли, что утверждение, что преподаватели–женщины получают в среднем меньшую зарплату по сравнению с преподавателями-мужчинами?

Вариант 6

В рабочей книге MS Excel ПреподКолледж.xls содержатся данных о заработной плате преподавателей колледжа. Верно ли, что утверждение, что преподаватели со степенью при поступлении на работу получают в среднем большую зарплату по сравнению с преподавателями без степени при поступлении на работу?

Вариант 7

В рабочей книге MS Excel ПреподКолледж.xls содержатся данные о заработной плате преподавателей колледжа. Верно ли, что утверждение, что преподаватели со степенью при поступлении на работу имеют в среднем больший возраст по сравнению с преподавателями без степени при поступлении на работу?

Вариант 8

Рабочая книга MS Excel ПреподЗатраты.xls содержит данные о заработной плате учителей, затратах в общественных школах в пересчете на одного ученика. Верно ли, что утверждение, что в среднем зарплата учителя в северных районах отличается от в среднем зарплаты учителя в остальных районах?

Вариант 9

Рабочая книга MS Excel ПреподЗатраты.xls содержит данные о заработной плате учителей, затратах в общественных школах в пересчете на одного ученика. Верно ли, что утверждение, что в среднем затраты в общественных школах в пересчете на одного ученика в южных районах отличается в среднем от затрат в остальных районах?

Вариант 10

Рабочая книга MS Excel ПреподЗатраты.xls содержит данные о заработной плате учителей, затратах в общественных школах в пересчете на одного ученика. Верно ли, что утверждение, что в среднем зарплата учителя в западных районах отличается от в среднем зарплаты учителя в остальных районах?

Вариант 11

Рабочая книга MS Excel ПреподЗатраты.xls содержит данные о заработной плате учителей, затратах в общественных школах в пересчете на одного ученика. Верно ли, что утверждение, что в среднем затраты в общественных школах в пересчете на одного ученика в западных районах отличается в среднем от затрат в остальных районах?

Вариант 12

В 1970 году распределение спортсменов среди спортивных команд (драфт) было организовано с помощью лотереи: 366 возможных дат рождения спортсменов были помещены во вращающийся барабан и выбраны случайным образом последовательно одна за другой. Первая выбранная дата получила номер 1, вторая – 2 и т.д. В рабочей книге MS Excel Драфт.xls содержатся данные о полученных таким образом номерах драфта. Верно ли, что утверждение, что, спортсмены, родившиеся во второй половине года в среднем имеют более низкие значения драфта чем спортсмены, родившиеся в первой половине года?

Вариант 13

В 1970 году распределение спортсменов среди спортивных команд (драфт) было организовано с помощью лотереи: 366 возможных дат рождения спортсменов были помещены во вращающийся барабан и выбраны случайным образом последовательно одна за другой. Первая выбранная дата получила номер 1, вторая – 2 и т.д. В рабочей книге MS Excel Драфт.xls содержатся данные о полученных таким образом номерах драфта. Верно ли, что утверждение, что, спортсмены, родившиеся во второй половине месяца в среднем имеют более низкие значения драфта чем спортсмены, родившиеся в первой половине месяца?

Вариант 14

Рабочая книга MS Excel Кредиты.xls содержит данные об отказах в выдаче кредита для 20 кредитных учреждений в зависимости от расы и уровня дохода. Предполагается, что кредитные учреждения гораздо чаще отказывают представителям национальных меньшинств. Проверьте обоснованность этого утверждения.

Вариант 15

Рабочая книга MS Excel Кредиты.xls содержит данные об отказах в выдаче кредита для 20 кредитных учреждений в зависимости от расы и уровня дохода. Предполагается, что кредитные учреждения гораздо реже отказывают клиентам с высоким уровнем доходов. Проверьте обоснованность этого утверждения.

Вариант 16

Рабочая книга MS Excel Кредиты.xls содержит данные об отказах в выдаче кредита для 20 кредитных учреждений в зависимости от расы и уровня дохода. Есть ли основание предполагать, что для представителей национальных меньшинств с большими доходами не существует дискриминации?

Cредство анализа надстройки «Пакет анализа» MS Excel «Двухвыборочный t-тест с одинаковыми дисперсиями»

Поиск по сайту