Математическая обработка

2.1 Определяем меру рассеивания М_р, мм по формуле:

 

где М 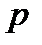- мера рассеивания, мм;

D - наибольший размер детали из контролируемой партии, мм;

D - наименьший размер детали из контролируемой партии, мм.

 

М_р = 12,02 – 11,91 = 0,11

 

Так как мера рассеивания превышает допуск размера, следовательно при

обработке имеет место брак.

 

2.2 Определяем среднее арифметическое значение размера каждой размерной группы D_ср.гр, мм:

 

 

D_ср.гр =

 

Результаты расчета вносим в графу 4 таблицы 1.

 

2.3 Определяем средний арифметический размер всех деталей партии D_ср, мм по формуле:

 

D_ср = ,

 

где m_i - количество деталей в размерной группе, шт;

Σm_i - количество деталей в контрольной партии, шт.

 

Числителем этой дроби является сумма данных графы 5 таблицы 1, а знаменателем – сумма данных графы 3 этой же таблицы.

 

В данном примере: D_ср = = 11,9656 мм.

 

2.4 Определяем среднее квадратичное отклонение σ, мм²:

 

,

 

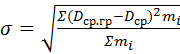где числителем дроби под корнем является сумма данных приведенных в графе 8 таблицы 1.

 

Для группы 1 получены следующие данные:

- в графе 6: ;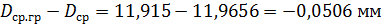

- в графе 7:

- в графе 8:

 

Аналогично выполняется расчет для всех размерных групп

 

01999899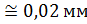

 

Принимаем σ = 0,02 мм

 

3. Построение кривых фактического и нормального распределения

3.1 Построение кривой нормального распределения

 

Для построения кривой нормального распределения по оси абсцисс откладываем значения размеров значения х, а по оси ординат – значения y. Для построения кривой достаточно 5-ти основных точек.

Определяем координаты пяти характерных точек, как показано в таблице 3.

Начало координат точка О соответствует среднеарифметическому размеру D_ср.

 

Таблица 3 – Определение координат характерных точек

Номер точки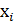
	=

 

 

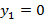
3.2 Построение кривой фактического распределения

 

По данным расчетной таблицы 1 строим кривую фактического распределения, откладывая по оси ординат значения m_i, а по оси абсцисс – значения D_ср.гр .

 

4. Определение процента возможного брака

В данном случае брак имеет место, так как поле рассеивания размеров детали (М_р = 0,11 мм) больше допуска размера детали (Т = 0,07 мм).

Расчет процента годных и бракованных деталей, с распределением последних на исправимый и неисправимый брак, производят в следующей последовательности:

1. Рассчитывают значения вспомогательных величин z₁ и z₂. При этом используют данные о допустимых предельных размерах D_max и D_min готовых деталей.

2. Для величин z₁ и z₂ из таблиц (приложение А) находят значения величин Ф₁ и Ф₂.

3. По величинам Ф₁ и Ф₂ определяют вероятность получения деталей с размерами меньшими, чем заданные и деталей с большими размерами, чем заданные.

Расчет сводим в таблицу 4.

 

Таблица 3 – Определение возможного брака

Вид брака	Определение z	Определе- ние Ф по таблице	Определение возмож- ного брака, %
Исправимый	z1 =	Ф1= 0,4573	Р1 = (0,5 – Ф1)100%
Неисправимый	z2 =	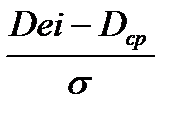Ф2= 0,4625	Р2 = (0,5 – Ф2)100%

Итого: годных деталей -?

брак -?

 

Контрольные вопросы:

1. Дайте определение понятию «точность».

2. Дайте определение понятию «погрешность».

3. Факторы, влияющие на точность обработки на металлорежущих станках.

4. Погрешности, возникающие в процессе обработки.

5. Дайте определение понятию «рассеивание размеров».

6. Какие факторы вызывают рассеивание размеров при обработке партии деталей на металлорежущих станках.

7. Расскажите об основных законах рассеивания размеров деталей машин используемых в машиностроении.

8. Что характеризует среднее квадратичное отклонение.

9. Что такое поле рассеивания и чем оно отличается от поля допуска.

10. Для чего рассчитывают и строят кривые распределения?

Приложение А «Таблица Лапласа»

 

Таблица значений функции Лапласа

z	Ф(x)	z	Ф(x)	z	Ф(x)	z	Ф(x)	z	Ф(x)	z	Ф(x)
0,00	0,00000	0,50	0,19146	1,00	0,34134	1,50	0,43319	2,00	0,47725	3,00	0,49865
0,01	0,00399	0,51	0,19497	1,01	0,34375	1,51	0,43448	2,02	0,47831	3,05	0,49886
0,02	0,00798	0,52	0,19847	1,02	0,34614	1,52	0,43574	2,04	0,47932	3,10	0,49903
0,03	0,01197	0,53	0,20194	1,03	0,34849	1,53	0,43699	2,06	0,48030	3,15	0,49918
0,04	0,01595	0,54	0,20540	1,04	0,35083	1,54	0,43822	2,08	0,48124	3,20	0,49931
0,05	0,01994	0,55	0,20884	1,05	0,35314	1,55	0,43943	2,10	0,48214	3,25	0,49942
0,06	0,02392	0,56	0,21226	1,06	0,35543	1,56	0,44062	2,12	0,48300	3,30	0,49952
0,07	0,02790	0,57	0,21566	1,07	0,35769	1,57	0,44179	2,14	0,48382	3,35	0,49960
0,08	0,03188	0,58	0,21904	1,08	0,35993	1,58	0,44295	2,16	0,48461	3,40	0,49966
0,09	0,03586	0,59	0,22240	1,09	0,36214	1,59	0,44408	2,18	0,48537	3,45	0,49972
0,10	0,03983	0,60	0,22575	1,10	0,36433	1,60	0,44520	2,20	0,48610	3,50	0,49977
0,11	0,04380	0,61	0,22907	1,11	0,36650	1,61	0,44630	2,22	0,48679	3,55	0,49981
0,12	0,04776	0,62	0,23237	1,12	0,36864	1,62	0,44738	2,24	0,48745	3,60	0,49984
0,13	0,05172	0,63	0,23565	1,13	0,37076	1,63	0,44845	2,26	0,48809	3,65	0,49987
0,14	0,05567	0,64	0,23891	1,14	0,37286	1,64	0,44950	2,28	0,48870	3,70	0,49989
0,15	0,05962	0,65	0,24215	1,15	0,37493	1,65	0,45053	2,30	0,48928	3,75	0,49991
0,16	0,06356	0,66	0,24537	1,16	0,37698	1,66	0,45154	2,32	0,48983	3,80	0,49993
0,17	0,06749	0,67	0,24857	1,17	0,37900	1,67	0,45254	2,34	0,49036	3,85	0,49994
0,18	0,07142	0,68	0,25175	1,18	0,38100	1,68	0,45352	2,36	0,49086	3,90	0,49995
0,19	0,07535	0,69	0,25490	1,19	0,38298	1,69	0,45449	2,38	0,49134	3,95	0,49996
0,20	0,07926	0,70	0,25804	1,20	0,38493	1,70	0,45543	2,40	0,49180	4,00	0,49997
0,21	0,08317	0,71	0,26115	1,21	0,38686	1,71	0,45637	2,42	0,49224	4,05	0,49997
0,22	0,08706	0,72	0,26424	1,22	0,38877	1,72	0,45728	2,44	0,49266	4,10	0,49998
0,23	0,09095	0,73	0,26730	1,23	0,39065	1,73	0,45818	2,46	0,49305	4,15	0,49998
0,24	0,09483	0,74	0,27035	1,24	0,39251	1,74	0,45907	2,48	0,49343	4,20	0,49999
0,25	0,09871	0,75	0,27337	1,25	0,39435	1,75	0,45994	2,50	0,49379	4,25	0,49999
0,26	0,10257	0,76	0,27637	1,26	0,39617	1,76	0,46080	2,52	0,49413	4,30	0,49999
0,27	0,10642	0,77	0,27935	1,27	0,39796	1,77	0,46164	2,54	0,49446	4,35	0,49999
0,28	0,11026	0,78	0,28230	1,28	0,39973	1,78	0,46246	2,56	0,49477	4,40	0,49999
0,29	0,11409	0,79	0,28524	1,29	0,40147	1,79	0,46327	2,58	0,49506	4,45	0,50000
0,30	0,11791	0,80	0,28814	1,30	0,40320	1,80	0,46407	2,60	0,49534	4,50	0,50000
0,31	0,12172	0,81	0,29103	1,31	0,40490	1,81	0,46485	2,62	0,49560	4,55	0,50000
0,32	0,12552	0,82	0,29389	1,32	0,40658	1,82	0,46562	2,64	0,49585	4,60	0,50000
0,33	0,12930	0,83	0,29673	1,33	0,40824	1,83	0,46638	2,66	0,49609	4,65	0,50000
0,34	0,13307	0,84	0,29955	1,34	0,40988	1,84	0,46712	2,68	0,49632	4,70	0,50000
0,35	0,13683	0,85	0,30234	1,35	0,41149	1,85	0,46784	2,70	0,49653	4,75	0,50000
0,36	0,14058	0,86	0,30511	1,36	0,41309	1,86	0,46856	2,72	0,49674	4,80	0,50000
0,37	0,14431	0,87	0,30785	1,37	0,41466	1,87	0,46926	2,74	0,49693	4,85	0,50000
0,38	0,14803	0,88	0,31057	1,38	0,41621	1,88	0,46995	2,76	0,49711	4,90	0,50000
0,39	0,15173	0,89	0,31327	1,39	0,41774	1,89	0,47062	2,78	0,49728	4,95	0,50000
0,40	0,15542	0,90	0,31594	1,40	0,41924	1,90	0,47128	2,80	0,49744	5,00	0,50000
0,41	0,15910	0,91	0,31859	1,41	0,42073	1,91	0,47193	2,82	0,49760
0,42	0,16276	0,92	0,32121	1,42	0,42220	1,92	0,47257	2,84	0,49774
0,43	0,16640	0,93	0,32381	1,43	0,42364	1,93	0,47320	2,86	0,49788
0,44	0,17003	0,94	0,32639	1,44	0,42507	1,94	0,47381	2,88	0,49801
0,45	0,17364	0,95	0,32894	1,45	0,42647	1,95	0,47441	2,90	0,49813
0,46	0,17724	0,96	0,33147	1,46	0,42785	1,96	0,47500	2,92	0,49825
0,47	0,18082	0,97	0,33398	1,47	0,42922	1,97	0,47558	2,94	0,49836
0,48	0,18439	0,98	0,33646	1,48	0,43056	1,98	0,47615	2,96	0,49846
0,49	0,18793	0,99	0,33891	1,49	0,43189	1,99	0,47670	2,98	0,49856