Повторение. Тема «Первообразная. Интегралы».
Первообразная
Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной.
Дифференцируемая функция 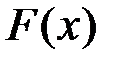 называется первообразной для функции
называется первообразной для функции  на заданном промежутке, если для всех х из этого промежутка справедливо равенство
на заданном промежутке, если для всех х из этого промежутка справедливо равенство  .
.
Из этого определения вытекает, что всякая функция по отношению к своей производной является первообразной.
Так, функция 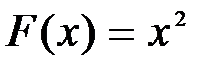 есть первообразная функции
есть первообразная функции 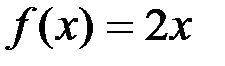 на интервале
на интервале  , поскольку для всех
, поскольку для всех  имеет место равенство
имеет место равенство  .
.
1. Найти первообразную функции 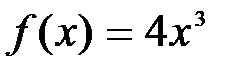 .
Решение: Используя правило дифференцирования, можно догадаться, что на интервале .
Решение: Используя правило дифференцирования, можно догадаться, что на интервале  первообразной является первообразной является  . Действительно, . Действительно,  для всех для всех 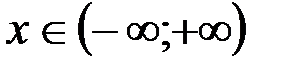 .
2. Найти первообразную функции .
2. Найти первообразную функции  на множестве R.
Решение: Степень на множестве R.
Решение: Степень  получается при дифференцировании получается при дифференцировании  . Так как . Так как  , то, чтобы при дифференцировании , то, чтобы при дифференцировании  получить перед получить перед  коэффициент 1, нужно коэффициент 1, нужно  взять с коэффициентом 1/7. Следовательно, взять с коэффициентом 1/7. Следовательно,  . .
|
Неопределенный интеграл
Как уже было отмечено, первообразную можно находить не только по данной ее производной, но и по ее дифференциалу. В дальнейшее мы будем этим пользоваться.
Определение. Совокупность всех первообразных  функции
функции  на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом
на рассматриваемом промежутке называется неопределенным интегралом и обозначается символом  , где
, где  - подынтегральная функция,
- подынтегральная функция, 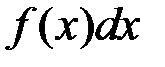 - подынтегральное выражение, х – переменная интегрирования.
- подынтегральное выражение, х – переменная интегрирования.
Таким образом, если 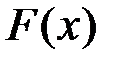 - какая-нибудь первообразная функции
- какая-нибудь первообразная функции  на некотором промежутке, то
на некотором промежутке, то  , где С – любое действительное число.
, где С – любое действительное число.
Замечание. Наличие постоянной С делает задачу нахождения функции по ее производной не вполне определенной; отсюда происходит название «Неопределенный интеграл».
Так, пользуясь определением неопределенного интеграла, можно записать:  .
.
Значит, чтобы найти неопределенный интеграл от заданной функции, нужно найти какую-нибудь одну из ее первообразных и прибавить к ней произвольную постоянную С.
1.Найти неопределенный интеграл  .
.
Решение: 
2. Найти интеграл  .
.
Решение: 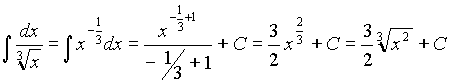
Определенным интегралом 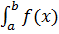 в пределах от а до в от функции f(x), непрерывной на отрезке [ а, в ], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=в:
в пределах от а до в от функции f(x), непрерывной на отрезке [ а, в ], называется приращение любой ее первообразной F(x) при изменении аргумента х от значения х=а до х=в:
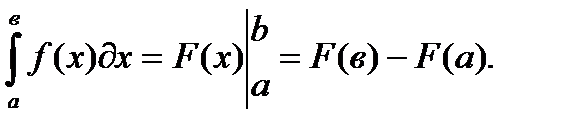
Данная формула так же называется формулой Ньютона-Лейбница, ее называют основной формулой интегрального исчисления.
Свойства определенного интеграла.
- Определенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определенных интегралов от слагаемых функций:

- Постоянный множитель можно выносить за знак определенного интеграла:

- При перестановке пределов интегрирования определенный интеграл меняет свой знак на противоположный:

- Определенный интеграл с одинаковыми пределами равен нулю:

- Отрезок интегрирования можно разбивать на части:
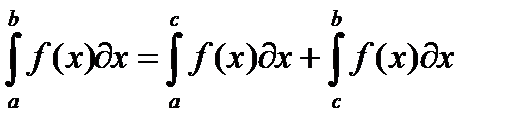
ПРИМЕРЫ: Вычислить интеграл:
1)  ;
;
2) 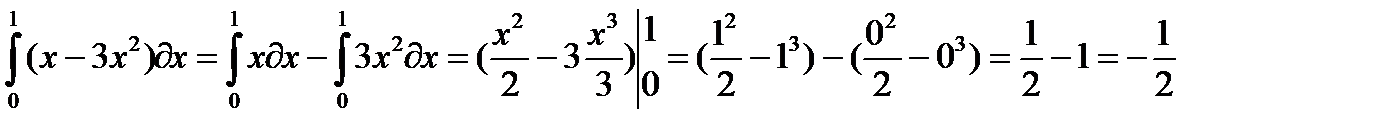 ;
;
3) 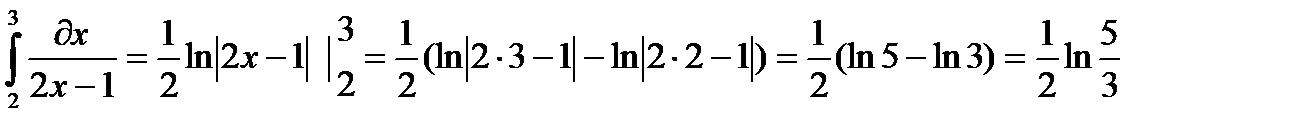 ;
;
4)  ;
;
Задание на дом. Домашняя работа.
1).Вычислите интегралы:
1.  2.
2. 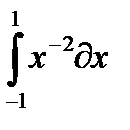 3.
3.  4.
4. 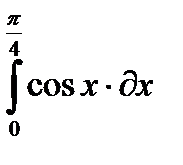 5.
5. 
2). Выполните тест:
Тест
Первообразная и интеграл.
А1. Выберите первообразную для функции 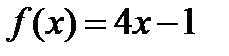 .
.
1)  2)
2) 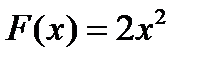 3)
3) 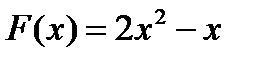 4)
4) 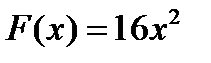
А2. Какая из данных функций не является первообразной для функции  ?
?
1) 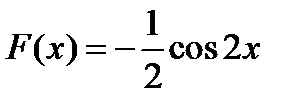 2)
2)  3)
3)  4)
4) 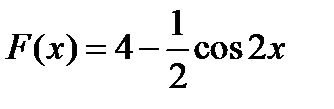
А3. Найдите общий вид первообразных для функции 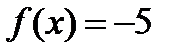 .
.
1)  2)
2)  3)
3) 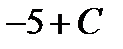 4)
4) 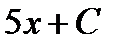
А4. Вычислите интеграл 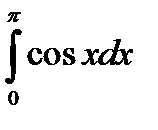 . 1)
. 1) 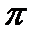 2)
2)  3)
3)  4)
4) 
А5. Вычислите интеграл 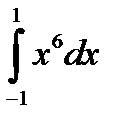 . 1)
. 1) 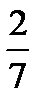 2)
2)  3)
3)  4)
4) 