Вращения.
Закон всемирного тяготения. Потенциал поля тяготения. Космические скорости.
Постулаты специальной (частной) теории относительности. Следствия СТО: длительность событий в разных системах отсчета, длина тел в разных системах отсчета и закон взаимосвязи массы и энергии.
Статистический и термодинамический методы. Температура. Опытные законы идеального газа.
Уравнение Клапейрона — Менделеева. Основное уравнение молекулярно-кинетической теории идеальных газов.
Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения.
14) Явления переноса в термодинамически неравновесных системах. Теплопроводность, диффузия и внутреннее трение.
Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы молекул.
Первое начало термодинамики. Работа газа при изменении его объема. Теплоемкость.
Уравнением Майера. Адиабатический процесс. Термический коэффициент полезного действия для кругового процесса.
Энтропия, ее статистическое толкование и связь с термодинамической вероятностью. Второе начало термодинамики.
Тепловые двигатели и холодильные машины. Цикл Карно и его к. п. д. для идеального газа.
Изотермы реальных газов. Фазовые переходы. Критическое состояние. Тройная точка фазового равновесия. Сжижение газов.
Электростатика. Закон Кулона. Электростатическое поле. Напряженность электростатического поля.
Линии напряженности электростатического поля. Теорема Гаусса для электростатического поля.
Работа по перемещению заряда в электростатическом поле. Потенциал электростатического поля. Циркуляцией вектора напряженности.
Типы диэлектриков. Поляризация диэлектриков. Напряженность поля в диэлектрике. Диэлектрической проницаемостью среды.
Проводники в электростатическом поле. Электростатическая индукция. Электрическая емкость уединенного проводника. Электроемкость конденсаторов.
Электрический ток, сила и плотность тока. Закон Ома. Сопротивление проводников. Работа и мощность тока. Закон Джоуля — Ленца.
Сторонние силы. Электродвижущая сила. Закон Ома для замкнутой цепи с ЭДС. Правила Кирхгофа для разветвленных цепей.
28) Магнитное взаимодействие элементов тока. Магнитное поле. Закон Био-Савара-Лапласа. Циркуляция вектора В магнитного поля в вакууме.
Поток вектора магнитной индукции. Теорема Гаусса для поля В. Явление электромагнитной индукции (опыты Фарадея).
Закона электромагнитной индукции Фарадея. Правило Ленца. Индуктивность контура. Самоиндукция.
Магнетики: диамагнетики парамагнетики и ферромагнетики. Магнитное поле в веществе. Магнитная проницаемость магнетика.
Основы теории Максвелла для электромагнитного поля. Ток смещения. Уравнения Максвелла для электромагнитного поля в интегральной форме.
Электромагнитные волны. Уравнение электромагнитной волны. Скорость распространения электромагнитных волн. Гармоническая волна. Связь периода колебаний и длины волны для гармонической волны
Свободные гармонические колебания в колебательном контуре. Переменный ток. Цеп переменного тока, содержащая последовательно включенные резистор, катушку индуктивности и конденсатор. Резонанс напряжений.
1)
Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. В механике сначала изучают движение одной материальной точки, а затем переходят к изучению движения системы материальных точек. Под воздействием тел друг на друга тела могут деформироваться, т. е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель — абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками этого тела остается постоянным. Положение материальной точки определяется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета — совокупность системы координат и часов, связанных с телом отсчета. Траектория движения материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.

Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути As и является скалярной функцией времени: Ds = Ds(t). Вектор Dr=r-r0, проведенный из начального положения движущейся точки в положение ее в. данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени), называется перемещением.
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения |Dr| равен пройденному пути Ds.
2)
Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.
Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r0. В течение малого промежутка времени Dt точка пройдет путь As и получит элементарное (бесконечно малое) перемещение Dr.
Вектором средней скорости <v > называется отношение приращения Dr радиуса-вектора точки к промежутку времени Dt:

Направление вектора средней скорости совпадает с направлением Dr. При неограниченном уменьшении Dt средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:

Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис. 3). По мере уменьшения Dt путь Ds все больше будет приближаться к |Dr|, поэтому модуль мгновенной скорости


Таким образом, модуль мгновенной скорости равен первой производной пути по времени:

При неравномерном движении модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной (v) — средней скоростью неравномерного движения:

Если выражение ds = vdt (2.2) проинтегрировать по времени в пределах от t до t+ D t, то найдем длину пути, пройденного точкой за время Dt:
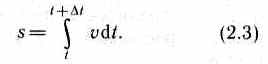
В случае равномерного движения числовое значение мгновенной скорости постоянно; тогда выражение (2.3) примет вид
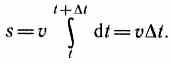
Длина пути, пройденного точкой за промежуток времени от t 1до t 2, дается интегралом

В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение. Средним ускорением неравномерного движения в интервале от t до t+ D t называется векторная величина, равная отношению изменения скорости Dv к интервалу времени Dt:
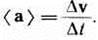
Мгновенным ускорением а (ускорением) материальной точки в момент времени t будет предел среднего ускорения:
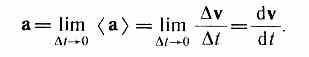
Таким образом, ускорение а есть векторная величина, равная первой производной скорости по времени. Тангенциальная составляющая ускорения

т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
Вторая составляющая ускорения, равная

называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.5):

Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения — быстроту изменения скорости по направлению (направлена к центру кривизны траектории).
3)
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени. Линейная скорость точки

В векторном виде формулу для линейной скорости можно написать как векторное произведение:
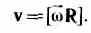
При этом модуль векторного произведения, по определению, равен 
, а направление совпадает с направлением поступательного движения правого винта при его вращении от w к R.
Если w=const, то вращение равномерное и его можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2p. Так как промежутку времени Dt=T соответствует Dj=2p, то w= 2p/Т, откуда

 связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение аt, нормальное ускорение а n) и угловыми величинами (угол поворота j, угловая скорость (о, угловое ускорение e) выражается следующими формулами:
связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение аt, нормальное ускорение а n) и угловыми величинами (угол поворота j, угловая скорость (о, угловое ускорение e) выражается следующими формулами:

4) Динамика является основным разделом механики, в ее основе лежат три закона Ньютона, сформулированные им в 1687 г. Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.
Механическое движение относительно, и его характер зависит от системы отсчета. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы. Первый закон Ньютона утверждает существование инерциальных систем отсчета. Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу с очень высокой точностью. Чтобы описывать воздействия, упоминаемые в первом законе Ньютона, вводят понятие силы. Под действием сил тела либо изменяют скорость движения, т. е. приобретают ускорения (динамическое проявление сил), либо деформируются, т. е. изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Итак, сила — это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. Второй закон Ньютона — основной закон динамики поступательного движения — отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. Второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). a = F /m,
или
F = m a = md v /dt. Векторная величина численно равная произведению массы материальной точки на ее скорость и имеющая направление скорости, называется импульсом (количеством движения) этой материальной точки. F =d p /dt. Это выражение — более общая формулировка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе. Выражение F =d p /dt называется уравнением движения материальной точки. Единица силы в СИ — ньютон (Н): 1 Н — сила, которая массе в 1 кг сообщает ускорение 1 м/с2 в направлении действия силы:
1 Н=1 кг•м/с2. Второй закон Ньютона справедлив только в инерциальных системах отсчета.механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было
5) Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
F 12=- F 2I,
где F 12 — сила, действующая на первую материальную точку со стороны второй; F 21 — сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы. Третий закон Ньютона позволяет осуществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками. Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой (или изолированной). Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т. е. геометрическая сумма внутренних сил равна нулю.
Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны т 1 ,m 2,..., тn и v 1, v 2,..., v n. Пусть F '1, F '2,..., F 'n — равнодействующие внутренних сил, действующих на каждое из этих тел, a f 1, f 2,..., F n — равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:
d/dt(m1v1)= F '1+ F 1,
d/dt(m2v2)= F' 2+ F 2,
d/dt)mn v n)= F 'n+ F n.
Складывая почленно эти уравнения, получим
d/dt (m1 v 1+m2 v 2+... + mn v n) = F '1+ F '2+...+ F ' n + F 1+ F 2+...+ F n.
Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то
d/dt(m1v1+m2v2 +... + mnvn)= F 1 + F 2+...+ F n, или
dp/dt= F 1+ F 2+...+ F n, (9.1)
где 
импульс системы. Таким образом, производная по времени от импульса механической системы равна геометрической сумме внешних сил, действующих на систему.
В случае отсутствия внешних сил (рассматриваем замкнутую систему)

Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон сохранения импульса — фундаментальный закон природы. В механике Галилея — Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс. Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен

где mi и ri — соответственно масса и радиус-вектор i-й материальной точки; n — число материальных точек в системе;
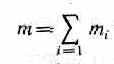
— масса системы.
Скорость центра масс
 центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
6) Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той или иной форме) одним телом другому телу, равна энергии, полученной последним телом.
Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы
количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол а с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs = Fcosa), умноженной на перемещение точки приложения силы:
A = Fss = Fs cosa. (11.1) В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения — прямолинейным. Элементарной работой силы F на перемещении d r называется скалярная величина
dА = F d r = F cosa• ds=Fsds,
где а — угол между векторами F и d r; ds = |d r | — элементарный путь; Fs — проекция вектора F на вектор d r. Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу

Для вычисления этого интеграла надо знать зависимость силы Fs от пути s вдоль траектории 1 — 2. Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой в 1 Н на пути в 1 м (1 Дж = 1 Н•м).
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
N=da/dt. (11.3)
За время dt сила F совершает работу F d r, и мощность, развиваемая этой силой, в данный момент времени
N= F d r /dt= Fv
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.
Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа в 1 Дж (1 Вт = 1 Дж/с).
Кинетическая энергия механической системы — это энергия механического движения этой системы.
Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии dT тела, т. е.
dA= dT.
Используя второй закон Ньютона F =md v /dt
и умножая обе части равенства на перемещение d r, получим
F d r =m(d v /dt)dr=dA

Таким образом, тело массой т, движущееся со скоростью v, обладает кинетической энергией
Т = тv2/2. (12.1)
Из формулы (12.1) видно, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения.
При выводе формулы (12.1) предполагалось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать законы Ньютона. В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета.
Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них,— консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; ее примером является сила трения.
Тело, находясь в потенциальном поле сил, обладает потенциальной энергией. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
dA=-dП. Потенциальная энергия может быть определена
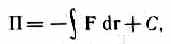
где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня. потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, равна
П = mgh, (12.7)
где высота h отсчитывается от нулевого уровня, для которого П0 = 0. Сила упругости пропорциональна деформации:
Fхупр=-kx,
где Fxупр— проекция силы упругости на ось х;k — коэффициент упругости (для пружины — жесткость), а знак минус указывает, что Fx направлена в сторону, противоположную деформации х. Потенциальная энергия системы, подобно кинетической энергии, является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
Полная механическая энергия системы — энергия механического движения и взаимодействия:
Е = Е+П,
т. е. равна сумме кинетической и потенциальной энергий. Закон сохранения энергии — результат обобщения многих экспериментальных данных. Идея этого закона принадлежит М. В. Ломоносову, изложившему закон сохранения материи и движения, а количественная формулировка закона сохранения энергии дана немецким врачом Ю. Майером и немецким естествоиспытателем Г. Гельмгольцем. При переходе системы из состояния 1 в какое-либо состояние 2

т. е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то следует, что
d(Т+П) = 0,
откуда
Т+П = E=const, (13.3)
т. е. полная механическая энергия системы сохраняется постоянной. Выражение (13.3) представляет собой закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.
Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Закон сохранения механической энергии можно сформулировать так: в консервативных системах полная механическая энергия сохраняется.
Закон сохранения механической энергии связан с однородностью времени, т. е. инвариантностью физических законов относительно выбора начала отсчета времени. Например, при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать.
Существует еще один вид систем — диссипативные системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации (или рассеяния) энергии. Строго говоря, все системы в природе являются диссипативными.
В консервативных системах полная механическая энергия остается постоянной. Могут происходить лишь превращения кинетической энергии в потенциальную и обратно в эквивалентных количествах, так что полная энергия остается неизменной.
7) Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку А приложения силы, на силу F. M = [ rF ]. Модуль момента силы M = Frsina= Fl, где a — угол между г и F; rsina = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы. Моментом силы относительно неподвижной оси z называется скалярная величина Мz, равная проекции на эту ось вектор а М момента силы, определенного относительно произвольной точки О данной оси 2. Значение момента Мz не зависит от выбора положения точки О на оси z.
Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:
М z = [ rF ]z. 
Уравнение (18.3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Можно показать, что если ось вращения совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство

где J — главный момент инерции тела (момент инерции относительно главной оси).
8) При изучении вращения твердого тела пользуются понятием момента инерции. Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

В случае непрерывного распределения масс эта сумма сводится к интегралу
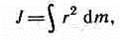
где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами х, у, z.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы mтела на квадрат расстояния а между осями: J = Jc + ma2.
При сравнении законов вращательного и поступательного движений просматривается аналогия между ними, только во вращательном движении вместо силы «выступает» ее момент, роль массы играет момент инерции. Какая же величина будет аналогом импульса тела? Ею является момент импульса тела относительно оси.
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
L = [ rp | = [ r m v ]. где r — радиус-вектор, проведенный из точки О в точку A; p = m v — импульс материальной точки; L —псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к p. Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса Lz не зависит от положения точки О на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса ri с некоторой
скоростью vi. скорость vi; и импульс m ivi
перпендикулярны этому радиусу, т. е. радиус является плечом вектора mi v i. Поэтому можем записать, что момент импульса отдельной частицы
Liz = тiviri (19.1)
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Используя формулу (17.1) vi = wri, получим

т. е.
Lz = Jzw. (19.2)
Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Это выражение - форма уравнения (закона) динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. В замкнутой системе момент внешних сил М =0 и d L /dt=0, откуда
L = const. (19.4)
Выражение (19.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Закон сохранения момента импульса — фундаментальный закон природы, Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).
При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi, опишут окружности различных радиусов ri и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
w = v 1 /r 1 = v 2 /r 2 =... = vn/rn. (17.1)
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:

или

Используя выражение (17.1), получим

где Jz — момент инерции тела относительно оси 2. Таким образом, кинетическая энергия вращающегося тела
Tвр = Jzw2/2. (17.2)
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела, движущегося поступательно (T= mv2/2), следует, что момент инерции вращательного движения — мера инертности тела. Формула (17.2) справедлива для тела, вращающегося вокруг неподвижной оси.
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:

где m — масса катящегося тела; vc — скорость центра масс тела; J с — момент инерции тела относительно оси, проходящей через его центр масс; w — угловая скорость тела.
9) Для объяснения петлеобразного движения планет древнегреческий ученый К. Птоломей (II в. н.э.), считая Землю расположенной в центре Вселенной, предположил, что каждая из планет движется по малому кругу (эпициклу), центр которого равномерно движется по большому кругу, в центре которого находится Земля. Эта концепция получила название птоломеевой геоцентрической системы мира и при поддержке католической церкви господствовала почти полторы тысячи лет. В начале XVI в. польским астрономом Н. Коперником (1473—1543) обоснована гелиоцентрическая система (см. § 5), согласно которой движения небесных тел объясняются движением Земли (а также других планет) вокруг Солнца и суточным вращением Земли. К началу XVII столетия большинство ученых убедилось, однако, в справ