Работа и мощность тока. Закон Джоуля — Ленца

Если сила тока выражается в амперах, напряжение — в вольтах, сопротивле­ние — в омах, то работа тока выражается в джоулях, а мощность — в ваттах. На практике применяются также внесистем­ные единицы работы тока: ватт-час (Вт•ч) и киловатт-час (кВт•ч). 1 Вт•ч — работа тока мощностью в 1 Вт в течение 1 ч: 1 Вт•ч = 3600 Вт•с = 3,6•10³ Дж; 1 кВт•ч=10³ Вт•ч = 3,6•10⁶ Дж.

Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии,

dQ=dA. (99.4)

Таким образом, используя выражения (99.4), (99.1) и (99.2), получим

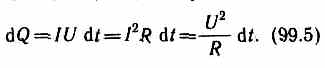
Выражение (99.5) представляет собой за­кон Джоуля — Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э. X. Ленцем.

Количество теплоты, выделяющееся за единицу времени в единице объема, на­зывается удельной тепловой мощностью тока. Она равна

w=rj². (99.6)

Используя дифференциальную форму за­кона Ома (j =gE) и соотношение r=1/g, получим

w = jE =g E ². (99.7)

Формулы (99.6) и (99.7) являются обоб­щенным выражением закона Джоуля — Ленца в дифференциальной форме, при­годным для любого проводника.

Тепловое действие тока находит широ­кое применение в технике, которое нача­лось с открытия в 1873 г. русским инжене­ром А. Н. Лодыгиным (1847—1923) лам­пы накаливания. На нагревании, про­водников электрическим током основано действие электрических муфельных печей, электрической дуги (открыта русским ин­женером В. В. Петровым (1761 — 1834)), контактной электросварки, бытовых элек­тронагревательных приборов и т. д.

27)

Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение носителей (они предполагаются положительными) от то­чек с большим потенциалом к точкам с меньшим потенциалом. Это приведет к выравниванию потенциалов во всех точках цепи и к исчезновению электричес­кого поля. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называ­ются источниками тока. Силы неэлектро­статического происхождения, действую­щие на заряды со стороны источников тока, называются сторонними.

Природа сторонних сил может быть различной. Например, в гальванических элементах они возникают за счет энергии химических реакций между электродами и электролитами; в генераторе — за счет механической энергии вращения ро­тора генератора и т. п. Роль источника тока в электрической цепи, образно гово­ря, такая же, как роль насоса, который необходим для перекачивания жидкости в гидравлической системе. Под действием создаваемого поля сторонних сил электри­ческие заряды движутся внутри источни­ка тока против сил электростатического поля, благодаря чему на концах цепи под­держивается разность потенциалов и в це­пи течет постоянный электрический ток.

Сторонние силы совершают работу по перемещению электрических зарядов. Фи­зическая величина, определяемая работой, совершаемой сторонними силами при пе­ремещении единичного положительного заряда, называется электродвижущей си­лой (э. д. с.) ξ, действующей в цепи:

ξ=A/Q ₀. (97.1)

Эта работа производится за счет энергии, затрачиваемой в источнике тока, поэтому величину ξможно также называть элек­тродвижущей силой источника тока, вклю­ченного в цепь. Напряжением U на участке 1 — 2 на­зывается физическая величина, определя­емая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении еди­ничного положительного заряда на дан­ном участке цепи.U₁₂=j₁-j₂+ξ₁₂.

Понятие напряжения является обоб­щением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует э.д.с., т. е. сторонние силы отсутствуют.

Закон Ома

Теперь рассмот­рим неоднородный участок цепи, где дей­ствующую э.д.с. на участке 1 — 2 обозна­чим через ξ₁₂, а приложенную на концах участка разность потенциалов — через

j₁-j₂.

Если ток проходит по неподвижным проводникам, образующим участок 1 — 2, то работа A ₁₂всех сил (сторонних и элек­тростатических), совершаемая над носите­лями тока, по закону сохранения и пре­вращения энергии равна теплоте, выделя­ющейся на участке. Работа сил, со­вершаемая при перемещении заряда Q₀ на участке 1 — 2, согласно (97.4),

A ₁₂ =Q₀ξ12 + Q ₀ (j ₁ -j₂). (100.1)

Э.д.с. ξ₁₂, как и сила тока I,— величи­на скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если

э.д.с. способствует движению положитель­ных зарядов в выбранном направлении (в направлении 1 — 2), то ξ₁₂>0. Если э.д.с. препятствует движению положитель­ных зарядов в данном направлении, то

ξ₁₂<0.

За время t в проводнике выделяется теплота (см. (99.5))

Q=I²Rt=IR(It)=IRQ₀. (100.2) Из формул (100.1) и (100.2) получим

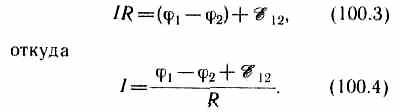
Выражение (100.3) или (100.4) представ­ляет собой закон Ома для неоднородного участка цепи в интегральной форме, кото­рый является обобщенным законом Ома.

Если на данном участке цепи источник тока отсутствует (ξ₁₂=0), то из (100.4) приходим к закону Ома для однородного участка цепи (98.1):

I =(j₁-j₂)/ R = U / R

(при отсутствии сторонних сил напряже­ние на концах участка равно разности потенциалов (см. §97)). Если же электри­ческая цепь замкнута, то выбранные точки 1 и 2 совпадают, j₁=j₂; тогда из (100.4) получаем закон Ома для замкнутой цепи:

I=ξ/R,

где ξ — э.д.с., действующая в цепи, R — суммарное сопротивление всей цепи. В общем случае R = r+R _1,где r — внут­реннее сопротивление источника э.д.с., R ₁ — сопротивление внешней цепи. По­этому закон Ома для замкнутой цепи будет иметь вид

I=ξ/(r+R₁).

Если цепь разомкнута и, следователь­но, в ней ток отсутствует (I=0), то из закона Ома (100.4) получим, что ξ₁₂=j₂-j₁ т. е. э.д.с., действующая в разо­мкнутой цепи, равна разности потенциа­лов на ее концах. Следовательно, для того чтобы найти э.д.с. источника тока, надо измерить разность потенциалов на его клеммах при разомкнутой цепи.

 

Правило Кирхгофа

Обобщенный закон Ома (см. (100.3)) по­зволяет рассчитать практически любую сложную цепь. Однако непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров (контуры могут иметь общие участки, каждый из контуров может иметь несколько источни­ков э.д.с. и т. д.), довольно сложен. Эта задача решается более просто с помощью двух правил Кирхгофа.

Любая точка разветвления цепи, в ко­торой сходится не менее трех проводников с током, называется узлом. При этом ток, входящий в узел, считается положитель­ным, а ток, выходящий из узла,— отрица­тельным.

Первое правило Кирхгофа: алгебраи­ческая сумма токов, сходящихся в узле, равна нулю:

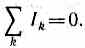
Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке про­водника и ни на одном его участке не должны накапливаться электрические за­ряды. В противном случае токи не могли бы оставаться постоянными.

I ₁ R ₁ -I ₂ R ₂ +I ₃ R ₃ = ξ ₁ - ξ ₂ + ξ ₃. (101.1)

Уравнение (101.1) выражает второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в развет­вленной электрической цепи, алгебраиче­ская сумма произведений сил токов I_i, на сопротивления R_i соответствующих участков этого контура равна алгебраиче­ской сумме э.д.с. ξ _k, встречающихся в этом контуре:

 

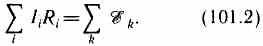
28) подобно тому, как в пространстве, окружающем электриче­ские заряды, возникает электростатиче­ское поле, так в пространстве, окружаю­щем токи и постоянные магниты, возника­ет силовое поле, называемое магнитным. Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные маг­ниты. Название «магнитное поле» связы­вают с ориентацией магнитной стрелки под действием поля, создаваемого током (это явление впервые обнаружено датским физиком X. Эрстедом (1777—1851)).

Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Важнейшая осо­бенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды. Опыт показывает, что характер воздействия магнитного поля на ток различен в за­висимости от формы проводника, по кото­рому течет ток, от расположения провод­ника и от направления тока. Следователь­но, чтобы охарактеризовать магнитное

поле, надо рассмотреть его действие на определенный ток.

Подобно тому, как при исследовании электростатического поля использовались точечные заряды, при исследовании маг­нитного поля используется замкнутый плоский контур с током (рамка с током), размеры которого малы по сравнению с расстоянием до токов, образующих маг­нитное поле. Ориентация контура в про­странстве характеризуется направлением нормали к контуру. В качестве положи­тельного направления нормали принима­ется направление, связанное с током пра­вилом правого винта, т. е. за положитель­ное направление нормали принимается направление поступательного движения винта, головка которого вращается в на-

правлении тока, текущего в рамке (рис. 160).

Опыты показывают, что магнитное поле оказывает на рамку с током ориентирую­щее действие, поворачивая ее определен­ным образом. Этот результат связывается с определенным направлением магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положи­тельная нормаль к рамке (рис. 161). За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует

на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса магнитной стрелки лежат в близ­ких точках поля, то силы, действующие на оба полюса, равны друг другу. Следо­вательно, на магнитную стрелку действу­ет пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направле­нием поля.

Рамкой с током можно воспользовать­ся также и для количественного описания магнитного поля. Так как рамка с током испытывает ориентирующее действие по­ля, то на нее в магнитном поле действует пара сил. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки:

М =[ р _m В ], (109.1)

где В — вектор магнитной индукции, яв­ляющейся количественной характеристи­кой магнитного поля, р_m — вектор магнит­ного момента рамки с током. Для плоского контура с током I

p _m = I S n, (109.2)

где S — площадь поверхности контура (рамки), n —единичный вектор нормали к поверхности рамки. Направление р _m

совпадает, таким образом, с направлением положительной нормали.

Магнитная индукция в данной точке однородного магнитного поля определяет­ся максимальным вращающим моментом, действующим на рамку с магнитным мо­ментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Следует отметить, что вектор В мо­жет быть выведен также из закона Ампера (см. §111) и из выражения для силы Лоренца (см. § 114).

Так как магнитное поле является сило­вым, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции — линий, касательные к кото­рым в каждой точке совпадают с направ­лением вектора В. Их направление зада­ется правилом правого винта: головка винта, ввинчиваемого по направлению то­ка, вращается в направлении линий маг­нитной индукции.

Линии магнитной индукции всегда за­мкнуты и охватывают проводники с током. Этим они отличаются от линий напряжен­ности электростатического поля, которые являются разомкнутыми (начинаются на положительных зарядах и кончаются на отрицательных (см. §79)).

На рис. 163 изображены линии магнитной индукции полосового магнита; они выходят из северного полюса и входят в южный. Вначале казалось, что здесь наблюдается полная анало­гия с линиями напряженности электростатичес­кого поля и полюсы магнитов играют роль магнитных «зарядов» (магнитных монополей). Опыты показали, что, разрезая магнит на части, его полюсы разделить нельзя, т. е. в отличие от электрических зарядов свободные магнитные «заряды» не существуют, поэтому линии маг­нитной индукции не могут обрываться на полю­сах. В дальнейшем было установлено, что внут­ри полосовых магнитов имеется магнитное поле, аналогичное полю внутри соленоида, и линии магнитной индукции этого магнитного поля яв­ляются продолжением линий магнитной индук­ции вне магнита. Таким образом, линии магнит­ной индукции магнитного поля постоянных магнитов являются также замкнутыми.

Вектор маг­нитной индукции В характеризует резуль­тирующее магнитное поле, создаваемое всеми макро- и микротоками, т. е. при одном и том же токе и прочих равных условиях вектор В в различных средах будет иметь разные значения.

Магнитное поле макротоков описыва­ется вектором напряженности Н. Для од­нородной изотропной среды вектор маг­нитной индукции связан с вектором на­пряженности следующим соотношением:

В =m₀m Н, (109.3)

где m₀ — магнитная постоянная, m — без­размерная величина — магнитная прони­цаемость среды, показывающая, во сколь­ко раз магнитное поле макротоков Н уси­ливается за счет поля микротоков среды. Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и Н) полей, укажем, что аналогом вектора напряженности электростатиче­ского поля Е является вектор магнитной индукции В, так как векторы Е и В опреде­ляют силовые действия этих полей и за­висят от свойств среды. Аналогом вектора электрического смещения D является век­тор напряженности Н магнитного поля.

Закон био-савара-лапласса

Магнитное поле постоянных токов различ­ной формы изучалось французскими уче­ными Ж. Био (1774—1862) и Ф. Саваром (1791 —1841). Результаты этих опытов бы­ли обобщены выдающимся французским математиком и физиком П. Лапласом.

Закон Био — Савара — Лапласа для проводника с током I, элемент которого d l создает в некоторой точке А (рис. 164) индукцию поля d B, записывается в виде

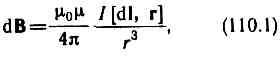
где d l — вектор, по модулю равный длине d l элемента проводника и совпадающий по направлению с током, r — радиус-вектор, проведенный из элемента d l проводника в точку А поля, r — модуль радиуса-векто­ра г. Направление d B перпендикулярно d l и r, т. е. перпендикулярно плоскости, в ко­торой они лежат, и совпадает с каса­тельной к линии магнитной индукции. Это направление может быть найдено по пра­вилу нахождения линий магнитной индук­ции (правилу правого винта): направле­ние вращения головки винта дает направ­ление d B, если поступательное движение винта соответствует направлению тока в элементе. Для магнитного поля, как и для элек­трического, справедлив принцип суперпо­зиции: магнитная индукция результирую­щего поля, создаваемого несколькими то­ками или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каж­дым током или движущимся зарядом в от­дельности:

Циркуляция вектора

Циркуляцией векто­ра В по заданному замкнутому контуру называется интеграл

где d l — вектор элементарной длины кон­тура, направленной вдоль обхода контура, В ₁= В cosa — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхо­да), а — угол между векторами В и d l.

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по про­извольному замкнутому контуру равна произведению магнитной постояннойm₀ на алгебраическую сумму токов, охватывае­мых этим контуром:

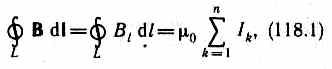
где n — число проводников с токами, ох­ватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается конту­ром. Положительным считается ток, на­правление которого связано с направлени­ем обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.

 

29) Потоком вектора магнитной индукции (магнитным потоком) через площадку d S называется скалярная физическая величи­на, равная

dФ_B= B d S =B_n dS, (120.1)

где B_n=В cosa — проекция вектора В на направление нормали к площадке dS (a — угол между векторами n и В), d S =dS n — вектор, модуль которого ра­вен dS, а направление совпадает с направ­лением нормали n к площадке. Поток век­тора В может быть как положительным, так и отрицательным в зависимости от знака cosa (определяется выбором поло­жительного направления нормали n). Обычно поток вектора В связывают с оп­ределенным контуром, по которому течет ток. В таком случае положительное на­правление нормали к контуру нами уже определено (см. §109): оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограничен­ную им самим, всегда положителен.

Поток вектора магнитной индук­ции Ф_B через произвольную поверхность S равен

единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий через плоскую поверхность площадью 1 м², рас­положенную перпендикулярно однородно­му магнитному полю, индукция которого равна 1 Тл (1 Вб=1 Тл•м²).

Теорема Гаусса для поля В: поток век­тора магнитной индукции через любую замкнутую поверхность равен нулю:

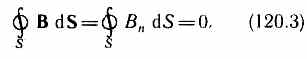
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

Электромагнитная индукция

Электрические токи создают вокруг себя магнитное поле. Связь магнитного поля с током привела к многочисленным попыткам возбудить ток в контуре с помощью магнитного поля. Эта фундаментальная задача была блестяще решена в 1831 г. английским физиком М. Фарадеем, открывшим явле­ние электромагнитной индукции, заключа­ющееся в том, что в замкнутом проводя­щем контуре при изменении потока маг­нитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного.

Рассмотрим классические опыты Фа­радея, с помощью которых было обнару­жено явление электромагнитной индукции.

Опыт 1. Если в замкнутый на гальванометр соленоид вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания наблюдается отклонение стрел­ки гальванометра (возникает индукционный ток); направления отклонений стрелки при вдвигании и выдвигании магнита противопо­ложны. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При изменении полюсов магнита направление отклонения стрелки изме­нится. Для получения индукционного тока маг­нит можно оставлять неподвижным, тогда нуж­но относительно магнита передвигать соленоид.

Опыт II. Концы одной из катушек, встав­ленных одна в другую, присоединяются к галь­ванометру, а через другую катушку пропускает­ся ток. Отклонение стрелки гальванометра на­блюдается в моменты включения или вы­ключения тока, в моменты его увеличения или уменьшения или при перемещении катушек друг относительно друга. Направления отклонений стрелки гальванометра также про­тивоположны при включении и выключении то­ка, его увеличении и уменьшении, сближении. и удалении катушек.

Обобщая результаты своих многочис­ленных опытов, Фарадей пришел к выводу, что индукционный ток возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции. Например, при повороте в однородном магнитном поле замкнутого проводящего контура в нем также возникает индукционный ток. В данном случае ин­дукция магнитного поля вблизи проводни­ка остается постоянной, а меняется только поток магнитной индукции через площадь контура.

Опытным путем было также установ­лено, что значение индукционного тока совершенно не зависит от способа измене­ния потока магнитной индукции, а опреде­ляется лишь скоростью его изменения (в опытах Фарадея также доказывается, что отклонение стрелки гальванометра (сила тока) тем больше, чем больше ско­рость движения магнита, или скорость изменения силы тока, или скорость движе­ния катушек).

Открытие явления электромагнитной индукции имело большое значение, так как была доказана возможность получе­ния электрического тока с помощью маг­нитного поля. Этим была установлена вза­имосвязь между электрическими и магнит­ными явлениями, что послужило в даль­нейшем толчком для разработки теории электромагнитного поля.

 

30) 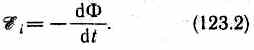Закон Фарадея можно сформулиро­вать еще таким образом: э.д.с. ξ _i элек­тромагнитной индукции в контуре числен­но равна и противоположна по знаку ско­рости изменения магнитного потока сквозь поверхность, ограниченную этим конту­ром. Этот закон является универсальным: э.д.с. ξ _i не зависит от способа изменения магнитного потока.

Э.д.с. электромагнитной индукции выражается в вольтах.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного по­тока, вызвавшего этот индукционный ток.