Рассмотрим произвольную контактную схему 
, реализующую логическую функцию 
. Пусть схема реализована на n элементах, и каждый из этих элементов может быть исправен или неисправен. Будем полагать, что вероятность выхода из строя более одного элемента одновременно настолько мала, что этот факт учитывать не будем. Тогда схема может находиться в двух состояниях – исправна или неисправна, если некоторый элемент 
вышел из строя. Выход из строя означает разрыв ребра , соответствующего данному элементу (контакту) в схеме, и это приводит к тому, что контактная схема будет реализовывать функцию 
. Очевидно, что среди всех 
могут найтись такие, что приводят к одним и тем же функциям. Тогда можно выделить классы эквивалентных состояний схемы 
, таких что 
. Поставим задачу об отыскании минимального числа тестов на наборах входных переменных схемы 
, обеспечивающего определение класса состояния, в котором оказалась система.
Рассмотрим, например, схему на рис 3.10.
Рис. 3.10. Пример контактной схемы
Эта схема реализует функцию
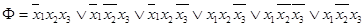. (3.25)
Пусть происходит выход из строя одного из 12 звеньев схемы. Каждая из таких ситуаций приводит к тому, что схема начинает реализовывать функции 
. Для конкретной схемы очевидно, что: 
.
Получаем семь классов эквивалентности:
, которые дают таблицу функций неисправностей (табл. 3.10). Пусть l равно числу классов эквивалентности (у нас l=7).
Таблица 3.10
| Наборы | 
| 
| 
| 
| 
| 
| 
| 
|
| 0 0 1 | |||||||
| 0 1 1 | |||||||
| 0 1 0 | |||||||
| 1 1 0 | |||||||
| 1 0 0 | |||||||
| 1 0 1 | |||||||
| 0 0 0 | |||||||
| 1 1 1 |
Свойство схемы, подлежащее определению, обычно задают через подмножество N пар (i,j) номеров классов функций неисправностей, которые требуется отличить. Если, например, 
, то свойство выражает отличимость исправной системы от неисправной (задача прверки). Если 
, то требуется отличать любые состояния схемы (задача диагностики). Наконец, если 
, то имеем дело с задачей о диагностике блока, т.е. в определении, в какой части схемы находится поврежденный элемент.
Совокупность наборов 
, где n – число переменных в схеме, называется тестом для данной таблицы функции неисправностей относительно подмножества N, если для любой пары 
существует набор 
такой, что 
. Тест называется минимальным, если он содержит минимальное число наборов. Тест Т называется тупиковым, если при удалении любого набора из Т получается подмножество наборов, не являющихся тестом. Множество 
является тестом (называется тривиальным тестом). Минимальный тест является тупиковым.
Существует алгоритм для нахождения всех тупиковых тестов. Пусть 
- множество всех наборов, на которых отличаются 
и 
. Если в выраженнии
(3.26)
где 
- элементы, составляющие , выполнить логическое умножение и затем удалить поглощаемые члены, воспользывавшись правилом 
, то оставшиеся произведения (конъюнкции) будут соответствовать тупиковым тестам. Так, если для рассмотренного примера решать задачу проверки схемы, то 
и указанный алгоритм дает:
Получим пять тупиковых тестов: 
. Из них 
и 
являются минимальными.
Этот алгоритм может быть применен для обнаружения ошибок при монтаже в соединениях элементов. Эффективность алгоритма резко падает с увеличением размерности таблицы функций неисправностей.
Задачи и упражнения
1. Используя метод карт Карно, найти минимальные ДНФ для функций, представленных изображающими числами:
а) # 0110101011011000, б) # 1110111010100000, в) # 1111010111110000, г) # 1110011010011100, д) # 1010111110100000.
2. Используя идеи минимизации ДНФ с помощью карт Карно обосновать и разработать метод минимизации КНФ.
3. Используя результаты задачи 2, найти минимальные КНФ для функций, представленных изображающими числами в задачах 1 a), б), в), г), д).
4. Упростить предварительно параллельные схемы (П-схемы), изображенные на рисунках:
5. Построить последовательно-параллельные контактные схемы (П-схемы), изображенные на рисунке.
6. Построить контактную схему с возможно меньшим числом элементов для функции, заданной изображающим числом:
а) # 0111101001101000, б) # 0010100111101101,
в) # 1001110011010010, г) # 0110110011010010, д) # 1010110011000101.
7. Построить для логической функции f (x 1, x 2, x 3) контактную схему и найти для этой схемы тупиковые и минимальные тесты в задаче проверки. Неисправность допускает не более одного разрыва контакта.
а) f (x 1, x 2, x 3) = # 10110110, б) f (x 1, x 2, x 3) = # 01110101, в) f (x 1, x 2, x 3) = # 10010101, г) f (x 1, x 2, x 3) = # 01101110,
д) f (x 1, x 2, x 3) = # 11010110.
8. Построить для функции f (x 1, x 2, x 3) контактную схему, найти тупиковые и минимальные тесты для задачи диагностики, если источник неисправностей допускает не более одного разрыва контакта.
а). f (x 1, x 2, x 3) = # 11100011, б) f (x 1, x 2, x 3) = # 01101101,
в) f (x 1, x 2, x 3) = # 11000111, г) f (x 1, x 2, x 3) = # 01011011,
д) f (x 1, x 2, x 3) = # 10011101.
9. Построить для функции f (x 1, x 2, x 3) контактную схему, найти все тупиковые и минимальные тесты для задачи проверки, если источник неисправностей допускает не более одного короткого замыкания контакта.
а). f (x 1, x 2, x 3) = # 01001100, б) f (x 1, x 2, x 3) = # 10010100,
в) f (x 1, x 2, x 3) = # 01100100, г) f (x 1, x 2, x 3) = # 10010010,
д) f (x 1, x 2, x 3) = # 00011100.