Техническую реализацию функций алгебры логики можно осуществить с помощью так называемых релейно-контактных схем. Исходным элементом в таких схемах является проводник, которому поставлена в соответствие логическая переменная х таким образом, что по проводнику идет ток или нет в зависимости от того х=1 или х=0. Тогда последовательному соединению проводников соответствует конъюнкция переменных, а параллельному – дизъюнкция (рис. 3.5).
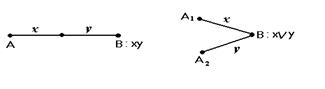
Рис.3.5. Элементарные схемы
Однако ясно, что таким способом, многократно используя параллельно-последовательные соединения, можно строить только монотонные функции. Для реализации произвольных функций достаточно суметь реализовать отрицания. Это можно сделать с помощью реле с размыкающим контактом (рис. 3.6а).

Рис.3.6. Размыкающее (а) и замыкающее (б) реле
Если х=0, т.е. на обмотку А ток не подается, то пружина D удерживает контакт замкнутым, и на выходе С имеем 1. Если х=1, то обмотка А размыкает контакт, и на выходе у нас 0. Т.е. реализована функция  . На рис. 3.6б изображено реле с замыкающим контактом, реализующем функцию х.
. На рис. 3.6б изображено реле с замыкающим контактом, реализующем функцию х.
Если на контакт В подавать не 1, а какую-то переменную, то рассмотренные схемы реализуют функции  и ху соответственно (рис. 3.7).
и ху соответственно (рис. 3.7).
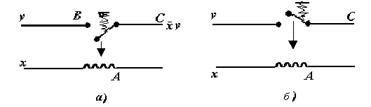
Рис.3.7. Реализация функций  и
и 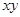
Для реализации дизъюнкции можем предложить чуть более сложную схему (рис. 3.8), работу которой достаточно просто проанализировать. Следует отметить, что, вообще говоря, эти схемы не являются однотактными. Так, в схемах рис. 3.7а и б, сигнал х подаётся в первый такт времени, реле срабатывает не мгновенно и наступает 2-й такт, когда на выходе появляется сигнал 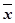 (или х). В схемах рис. 3.7а и б в 1-ом такте подаётся на вход х, а в следующем такте подаётся на вход сигнал у и мгновенно реализуется результат
(или х). В схемах рис. 3.7а и б в 1-ом такте подаётся на вход х, а в следующем такте подаётся на вход сигнал у и мгновенно реализуется результат  (или ху).
(или ху).
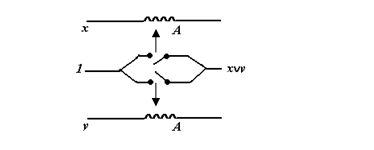
Рис.3.8. Реализация дизъюнкции
Таким образом, в зависимости от сложности схемы с некоторым запаздыванием 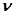 тактов на выходе реализуется функция
тактов на выходе реализуется функция 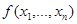 , причем последовательные наборы сигналов обрабатываются независимо.
, причем последовательные наборы сигналов обрабатываются независимо.
Рассмотрим схемы, в которых соединяются лишь контакты (нет соединений обмоток реле с контактами). Такие схемы называются просто контактными. В схеме контакт будем изображать отрезком, концы которого называют полюсами, а сам отрезок двухполюсным. Двухполюсник будем снабжать символом переменной  , если контакт замыкающий, и
, если контакт замыкающий, и  , если он размыкающий;
, если он размыкающий;  – переменная, которая реализуется на соответствующей обмотке реле. Считаем, что каждой переменной соответствует одна обмотка, с которой связано некоторое число контактов.
– переменная, которая реализуется на соответствующей обмотке реле. Считаем, что каждой переменной соответствует одна обмотка, с которой связано некоторое число контактов.
Тогда контактная схема представляет из себя граф (совокупность точек (полюсов), соединенных отрезками (дугами графа)). Ребрам приписаны символы логических переменных или их отрицаний. Ребра соответствуют контактам. Выделяют в схеме вход и выход. На вход подается ток, который распространяется по замкнутым в данный момент контактам. Если на выходе схемы появился ток, то проводимость схемы равна 1, в противном случае – 0. Логическая функция, определяющая зависимость проводимости от наборов переменных, называется функцией проводимости:

Каждой последовательно-параллельной контактной схеме можно поставить в соответствие логическую формулу, реализующую функцию проводимости. Две схемы считаются эквивалентными, если их функции проводимости совпадают. Тогда для сложных контактных схем можно использовать равносильности алгебры логики и упростить схемы, сокращая число контактов.
Например, для схемы (рис 3.9а) можем, используя законы последовательного и параллельного соединения контактов, для функции проводимости записать:


Рис. 3.9. Пример контактной схемы и упрощенной эквивалентной схемы
Упрощенная эквивалентная схема изображена на рис. 3.9б.