Этот метод включает в себя два этапа – преобразование исходной функции к сокращенной форме с помощью операции склеивания и получения минимальной формы путем исключения избыточных простых импликант.
Преобразование булевых формул путем склеивания удобно выполнять в символическом виде, где минтермы записываются в столбцы словами длины n, буквы которых соответствуют всем переменным данной функции. Входящие в минтерм переменные называются связанными и представляются значениями, при которых минтерм равен единице (1 для 
и 0 для 
). Не входящие в минтерм переменные являются свободными и обозначаются через x. Минтермы n-го порядка канонической формы представляются просто наборами значений переменных, на которых функция равна 1.
При склеивании пары минтермов n-го ранга, отличающихся только значениями переменной , появляется минтерм (n-1)-го ранга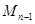 
, который входит в качестве сомножителя в исходные минтермы, т.е. + = ( +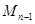 
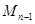
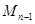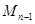)= . При этом представляющий его символ получается замещением в символе склеивания минтерма значения переменной на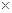 
. Аналогично склеивание пары минтермов (n-2)-го ранга с двумя свободными переменными и т.д. Принято говорить, что склеиваемые минтермы покрываются результирующими минтермами более низкого порядка.
Чтобы уменьшить число сравниваемых пар, целесообразно разбить множество минтермов на классы, в каждом из которых содержатся символы с одинаковым числом единиц (или нулей), и упорядочить эти классы по возрастающему (или убывающему) числу единиц. Т.к. объединяться могут только такие минтермы, символы которых содержат только на одну больше (или меньше) единиц, то достаточно ограничиться попарным сравнением символов соседних классов. Рассмотрим в качестве примера функцию четырех переменных, которую зададим таблицей
| X1 | ||||||||||||||||
| X2 | ||||||||||||||||
| X3 | ||||||||||||||||
| X4 | ||||||||||||||||
| Y |
Множество символов минтермов этой функции после упорядочения и разбиения на классы представляет собой минтермы канонической формы:
минтермы
1 2 3 4 5 6 7 8
Объединяя минтермы в М4 (1-й с 3-м, 1-й с 5-м, 2-й с 6-м, 2-й с 7-м, 3-й с 6-м, 3-й с 8-м, 4-й с 8-м, 5-й с 8-м) и обозначая символом 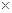«сокращаемую» переменную, получим М3, а затем, объединяя минтермы в М3 (1-й с 9-м и, 2-й с 7-м) и точно также обозначаем символом 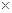«сокращаемую» переменную, получим М2. Отмечая (значком Ú) те из них, которые покрываются минтермами низшего ранга, в нашем случае минтерму М2 покрывают 1-й, 2й, 7-й, 9-й минтермы из М3, имеем
; 
.
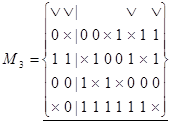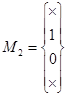1 2 3 4 5 6 7 8 9
Неотмеченные (символом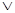 
) импликанты соответствуют простым импликантам сокращенной формы 
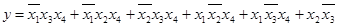. Для минимизации этой формы строится таблица покрытий, столбцы ко-торой соответствуют минтермам канонической формы, а строки – простым импликантам (табл. 3.8.).
Таблица 3.8
| Простые импликанты | Минтермы канонической формы | Обозначения простых импликант | |||||||
| 0X 11 | Ú | Ú | A | ||||||
| 01 X1 | Ú | Ú | B | ||||||
| X0 11 | Ú | Ú | C | ||||||
| 10 X1 | Ú | Ú | D | ||||||
| 1X 01 | Ú | Ú | E | ||||||
| X1 0X | Ú | Ú | Ú | Ú | F |
В таблице меткой Ú отмечены те минтермы, которые покрываются простыми импликантами. При переходе от сокращенного покрытия к минимальному следует прежде всего выделить те импликанты, называемые экстремалями, которые покрывают минтермы данной функции, не покрываемые никакими другими импликантами. Экстремали соответствует та строка таблицы, которая содержит единственную метку в каком-либо столбце.
В рассматриваемом примере единственная экстремаль представлена символом (X10X), которому соответствует минтерм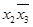 
. Удаляя строки экстремалей и все столбцы, в которых эти строки имеют метки, получаем более простую таблицу (табл.3.9)
Таблица 3.9
| Простые импликанты | Минтермы канонической формы | Обозначения простых импликант | |||
| 0X 11 | Ú | Ú | A | ||
| 01 X1 | Ú | B | |||
| X0 11 | Ú | Ú | C | ||
| 10 X1 | Ú | Ú | D | ||
| 1X 01 | Ú | E |
На основе этой таблицы выбираем простые импликанты, которые дополняют выделенное множество экстремалей (ядро покрытия) до минимального покрытия функции. В данном случае целесообразно выбрать простые импликанты (0X11) и (10X1), которые совместно с экстремалью (X10X) и образуют минимальное покрытие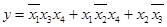 
.
Полный перебор всевозможных тупиковых форм с целью выделения минимальных форм для функций с большим числом переменных практически нереален вследствие комбинаторной сложности метода. Поэтому используются приближенные методы. Так, в минимаксном алгоритме включение в минимизирующую форму очередной импликанты осуществляется по правилу: выбирается столбец таблицы покрытий с наименьшим количеством меток и среди строк, имеющих в этом столбце метки, выбирается строка с наибольшим числом меток, которая и определяет требуемую импликанту, причем все минтермы, покрываемые этой импликантой, а значит, и соответствующие им столбцы, вычеркиваются. Процедура повторяется до тех пор, пока не будут вычеркнуты все столбцы.