Минимизация в классе дизъюнктивных нормальных форм

Мы уже показали, что произвольную логическую функцию можно всегда представить формулой в дизъюнктивной и конъюнктивной нормальной форме. Равносильными преобразованиями можно получить формулу, содержащую меньшее, чем исходная, число переменных. Например:

;

;

.

Отметим, что последнее преобразование уменьшает число вхождений переменных в формулу, но выводит формулу из класса ДНФ.

ДНФ называется минимальной, если она содержит наименьшее число вхождений переменных по сравнению со всеми равносильными ей ДНФ. Решение задачи минимизации может быть осуществлено просто методом перебора, что при значительном числе переменных, конечно, неэффективно. Существуют различные методы минимизации: метод минимизирующих карт, графический метод, основанный на картах Карно, алгоритм Квайна - МакКласки.

Из них мы сначала рассмотрим как наиболее простой метод минимизирующих карт и затем как один из наиболее распространённых и эффективных - метод карт Карно, а в конце алгоритм Квайна - МакКласки.

Метод минимизирующих карт

Пусть логическая функция задана таблицей истинности и СДНФ. Составим карту, представленную в таблице 3.6.Тогда справедливо утверждение.

Если конъюнкция , , , принадлежащая - й строке таблицы 3.6 не входит в СДНФ рассматриваемой функции , то любая конъюнкция - й строки не входит ни в какую ДНФ, выражающую эту функцию.

Таблица 3.6

			...			...		...	...
			...			...		...	...
			...			...		...	...
...	...	...	...	...	...	...	...	...	...
			...			...		...	...

Действительно, если конъюнкция не входит в СДНФ функции , то по формуле построения СДНФ (3.3) следует, что если бы какая-то конъюнкция -й строки вошла в некоторую ДНФ, то , а это противоречит исходному условию невхождения в СДНФ.

Чтобы показать это введем понятие импликанты. Формула 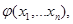называется импликантной если - элементарная конъюкция и , т.е.

Импликанта называется простой, если она не поглощается другой импликантой. Например для дизъюнкции рассмотрим таблицу истинности с импликантами. Стрелками указаны

Таблица 3.6

вхождение импликанты и, таким образом, можем записать

Из таблицы видно, что импликанты не являются простыми, так как они поглощаются простой импликантой (2-я и 3-я) и простой импликантой (1-я импликанта), тогда

Дизъюнкция простых импликант называется сокращенной ДНФ. После упращения сокращенной ДНФ получают тупиковую ДНФ. Упрощения могут быть разнообразными и поэтому тупиковых форм может бить несколько. Среди тупиковых форм находятся и минимальные.

В нашем случае в примере мы получили сокращенную форму, которая является и тупиковой и минимальной.

Тогда построение минимальной ДНФ осуществим следующим образом:

1. Отметим в таблице 3.6 строки, в которых соответствующая конъюнкция не принадлежит СДНФ. Вычеркнем все конъюнкции в этих строках.

2. Все вычеркнутые конъюнкции вычеркнем также во всех остальных строках.

3. В каждой строке выберем из оставшихся конъюнкций только те, которые содержат наименьшее число “сомножителей”, а остальные вычеркнем.

4. В каждой строке выберем по одному оставшемуся элементу и составим из них ДНФ.

5. Из всех ДНФ, полученных в п.4, выберем минимальную.

Перебор ДНФ, осуществляемый в п.5, производится среди много меньшего числа ДНФ, чем при простом переборе всех возможных ДНФ.

В качестве примера рассмотрим функцию с её CДНФ:

Построим таблицу 3.7. В этой таблице, вычеркнутые на этапах 1,2 элементы выделены, а вычеркнутые на этапе 3-. Тогда из оставшихся конъюнкций составим ДНФ:

x ₁ Ú x ₁ Ú x ₁ Ú x ₃ = x ₁ Ú x ₁ Ú x ₃;

x ₁ Ú x ₃ Ú x ₁ Ú x ₃ = x ₁ Ú x ₁ Ú x ₃;

x ₁ x ₃ Ú x ₁ Ú x ₁ Ú x ₃ = x ₁ Ú x ₁ Ú x ₃;

x ₁ Ú Ú x ₁ Ú x ₃ = x ₁ Ú x ₃.

Очевидно, что последняя ДНФ является минимальной.

Таблица 3.7

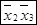
Построение минимизирующих карт для N=4 уже ёмкая работа по оформлению таблицы размером в 16 строк и 15 столбцов, и в этом случае можно воспользоваться следующим методом.

Метод карт Карно

Карты Карно - это специально организованные таблицы соответствия, на которых удобно производить операции склеивания или упрощения функции на пути к минимальным формам. Столбцы и строки этих таблиц соответствуют всем наборам значений переменных, причём эти наборы расположены в таком порядке, что каждый последующий (соседний) отличается от предыдущего значением только одной из переменных. Краевые ячейки таблиц тоже считаются “соседними”. На рис. 3.3 показаны карты Карно для функций с числом переменных N=2,3,4.

(X1, X2)

00 01 11 10

а)

б) в)

Рис 3.3 Карты Карно для функций двух (а), трех (б) и

четырех (в) переменных

Каждому набору значений переменных соответствует своя ячейка, в которую записывается 1 или 0 в соответствии с таблицей истинности или СДНФ. Зачастую 0 не записывается, и ячейку оставляют пустой.

На рис. 3.3 б) показана заполненная карта для функции трех переменных из предыдущего раздела. Операция склеивания состоит в объединении соседних ячеек, как показано на рисунке 3.3б. Число объединяемых ячеек всегда есть , - целые числа пар ячеек по горизонтали и вертикали.

Считывание карт Карно осуществляется последовательным рассмотрением групп ячеек. В ДНФ входят только те переменные, которые сохраняют свои значения в данной группе, причём значениям 1 соответствует сама переменная, 0 - её отрицание. Так для рисунка 3.3б. получим минимальную ДНФ:

,

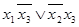в которой первая конъюнкция соответствует горизонтальной группе, а вторая - вертикальной. Уменьшить число вхождений переменных уже невозможно. Полученный результат соответствует решению, полученному методом минимизирующих карт. Для иллюстрации работы с функциями 4-х переменных рассмотрим функцию:

,

которая на карте Карно представлена на рисунке 3.4а.

На рисунке 3.4 б-д показаны все возможные объединения ячеек, среди которых можно получить минимальное “покрытие”, содержащее минимальное число вхождений переменных. Для вариантов объединения, представленных на рис 3.4 б-д, используя правило чтения карт Карно, получим ДНФ:

б) ;

в) ;

г) ;

д) .

Очевидно, что вариант “б” даёт минимальную ДНФ.

Для функций с числом переменных более четырёх возникают затруднения, связанные с необходимостью рассмотрения “колоды” карт Карно. Так, для N=5 необходимы 2 карты, на первой из которых X₅ = 0, а на второй X₅ =1, для N = 6 потребовалось бы 4 карты Карно и т. д.

Поскольку алгоритмы построения минимальных ДНФ довольно сложны, применяют алгоритмы упрощения, позволяющие получать приемлемые для дальнейшего использования ДНФ, среди которых содержатся и минимальные.

Сокращенная ДНФ формулы может быть получена, например, по следующему алгоритму. Рассмотрим произвольную конъюнктивную нормальную форму исходной формулы. Воспользуемся законом дистрибутивности

и “раскроем” скобки. Затем произведем упрощение полученной формулы, пользуясь равносильностями , и удаляя тождественно-ложные дизъюнктивные члены. В результате получим ДНФ, которая является сокращенной.

В приложениях булевой алгебры часто вводят понятие минтерма и макстерма. Минтерм - это элементы СДНФ (или ДНФ), представляющие собой элементарные конъюнкции, т.е. СДНФ (или ДНФ) - это дизъюнкция минтермов. Макстерм - это элементы СКНФ (или КНФ), т.е. СКНФ (или КНФ) - это конъюнкция макстермов.

При попытке получения минимальных форм процедуры склеивания минтермов обеспечивают преобразования к сокращенной форме, минтермы которой являются простыми импликантами. Если среди простых импликант сокращенной формы найти избыточные, которые покрываются совокупностями других импликант, то после их удаления получим тупиковую ДНФ.

Для каждой функции существует единственная сокращенная форма и может быть по несколько тупиковых и минимальных форм.

Рис. 3.4 Минимизация на картах Карно