Оглавление
1. Введение
2. Пропорция
3. Золотое сечение
4. Фракталлы
5. Перспектива
6. Проецирование
7. Золотая спираль.
8. Симметрия.
9. «Странные» свойства изображения.
10. Геометрические формы.
11. Исследовательскаяработа
12. Заключение
13. Литература
Введение
Математика владеет не только истиной, но и высшей красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Б. Рассел
Математика – это царица всех наук, её красоте, мудрости, стройности и гармонии можно только бесконечно удивляться и восхищаться. Искусство – это точное соблюдение законов математики, гармония, пропорциональность, творческое вдохновение, художественное мастерство. Законы математики действуют даже в тех областях, где их менее всего ожидалось встретить: в живописи, музыке, скульптуре. Исторически, математика играла важную роль в изобразительном искусстве, в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая - аналитическая, вторая - эмоциональная. Проект «Математика и живопись» позволяет проследить взаимосвязь живописи с законами математики, которые присутствуют в окружающем мире, управляют этим миром.
Я считаю, что изучение этого вопроса позволит шире взглянуть на окружающий мир, ещё и ещё раз поразиться неразрывному сочетанию науки и искусства, пополнить свой багаж знаний.
Главной целью данного проекта является попытка сформировать убеждение в том, что математика, искусство и красота – понятия неразделимые. Вообще-то не существует каких-либо правил или ограничений на использование различных в математическом искусстве. Однако, есть несколько тем, которые достаточно часто различным художниками. Среди них есть использование многогранников, тесселяций, невозможных фигур, лент Мебиуса, искаженных или необычных систем перспективы, а также фракталов.
Объект исследования: живопись и математика.
Предмет исследования: взаимосвязь живописи с законами математики, которые присутствуют в окружающем мире.
Цель моей работы:
· изучение математических законов, влияющих на изобразительное искусство
В связи с этой целью, необходимо было решить следующие задачи:
· Найти элементы математики, влияющие на живопись.
· Изучить влияние выявленных элементов на живопись.
Для решения поставленных задач были использованы следующие методы:
· сбор, исследование и анализ материала по данной теме.
· описание, обобщение сведений об атмосфере в жилищах.
Пропорция
Пропорция - равенство отношений числовых величин, т. е. равенство вида a: b = c: d, или, в других обозначениях, равенство 
Одной из задач при изображении объектов является изобразить их соразмерно, то есть пропорционально.
Пропорции в теле человека
В Древнем Египте были разработан первый в истории канон пропорции, где за единицу измерения была принята длина среднего пальца руки. Такая система позволяла делить изображение на части и по одной из них востанавить всю фигуру человека. Фигура имела высоту 21 часть, из которых 19 приходились на тело а остальные на головной убор
Художники пользовались специальной сеткой, деливещй плоскость на части, также были разработаны правила изображения сидячих фигур и богов, согласно их положению в древнеегипетском пантеоне. ()дполнить(
Дальнейшем в древней Греции была разработана другая система пропорций тела, золотое сечение. Во время эпохи возрождения художники снова стали изучать пропорции тела, Это вопрос изучал и Леонардо Да Винчи, по этому поводу он писал: «многие художники, которые изучают пропорции и размеры человеческого тела, не исследуют его разнообразия. Человек может быть пропорциональным будучи высокого роста, среднего, низкого; кто не считается с этим разнообразием - тот заслуживает самого большого осуждения»
Однако надо сказать, что не все люди имеют идеальные пропорции. Они появились в результате длительной работы многих гениальных художников древней Греции.
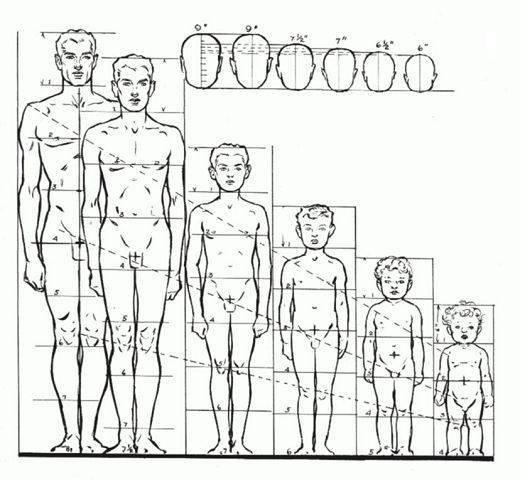
В среднем рост среднего человека равен 8 его головам, ширена плеч у мужчины 3 головы а у женщины в среднем 2.
Отношение ширены лица и 1 глаза 1/5.
Однако надо учитывать, что тело ребёнка имеет другие пропорции.
Золотое сечение
Золотое сечение было известно еще в древности. Так, в книге II «Начал» Евклида оно применяется при построении правильных пяти - и десятиугольников.
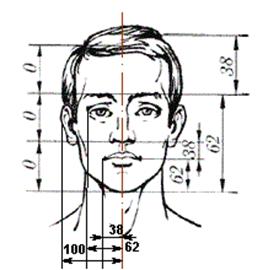
Термин «золотое сечение» ввел Леонардо да Винчи. «Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отметим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека относится к длине от пояса до ступней.… Если теперь измерим длину от макушки до среднего пальца, когда руки опущены по швам, то эта величина по отношению к расстоянию от среднего пальца до ступни составит то же число, что и отношение всего роста».
Действительно, в природе и человеческом теле много пропорциональных отношений, близких к тому, которое Леонардо назвал золотым сечением, хотя и не воплощающих его точно. Золотое сечение не единственное отношение, зрительно воспринимаемое как красивое. К их числу относятся такие отношения, как 1:Ö2, 1:Ö3. Они близки к золотому сечению. В любом произведении искусства несколько неравных, но близких к золотому сечению частей дают впечатление развития форм, их динамики, пропорционального дополнения друг друга.
В живописи и скульптуре храмов, на предметах домашнего обихода древние египтяне чаще всего изображали богов и фараонов. Были установлены каноны (законы) изображения стоящего человека, идущего, сидящего, коленопреклоненного и т. д. По особым правилам рисовали и священный цветок лотоса, и священных животных. Художники обязаны были заучивать отдельные формулы и схемы изображения по таблицам и образцам. Канон для изображения человеческой фигуры был разработан путем изучения и измерения как всей фигуры, так и каждой ее части (рис. 1).
|
Рис. 1.
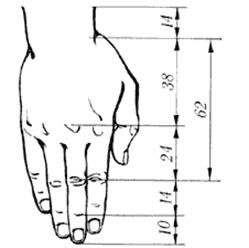
При этом использовалась такая система пропорционального членения фигуры на части, которая позволяла по части определить целое и по одной части тела определить размер другой. Диодор Сицилийский указывал, что египтяне «разделяли человеческое тело на 21,25 части и на основании этого регулировали всю экономию произведения». Это число, полученное вроде бы неизвестно откуда, долгое время заставляло ученых сомневаться в правильности сообщения Диодора. И только благодаря изысканием египтолога Лепсиуса эти сведения стали понятными. Лепсиус нашел в Египте рисунок человеческой фигуры, которая была изображена стоящей прямо, лицом вперед, и тело этой фигуры было разделено параллельными горизонтальными линиями на 21, 25 части. Единицей измерения служила длина среднего пальца руки. Само тело человека разделено на 19 равных частей, 2,25 части приходятся на традиционный головной убор фараонов.
Учеными позже было установлено, что по египетскому канону фигура человека имела следующие размеры: высота стопы считалась равной длине среднего пальца руки, расстояние от верхней части коленной чашечки до лобка – длине четырех пальцев и т. д. Для всех частей тела была определена точная вершина: ширина носа, глаз, рта, груди, толщина руки в различных местах и т. д.
Этот канон давал возможность ваятелю при изображении фигуры очень больших размеров (колосса) по величине целого судить о размерах какой-либо части – о размере всей фигуры. Известно, что египетские скульпторы лепили колоссов по частям, т. е. каждую часть одной и той же фигуры выполняли несколько мастеров порознь, порой даже в разных местах. Но когда готовые части складывались вместе, то они точно сходились без нарушения пропорций.
В художественных произведениях Древнего Египта часто встречается золотое сечение – деление отрезка, при котором одна его часть во столько же раз больше другой, во сколько сама она меньше целого.
На основе этого соотношения созданы пропорции древнеегипетского канона – восемь пропорциональных величин. Они получены следующим образом. Каждую сторону квадрата делили в золотом отношении, считая сначала от точки А, а потом от точки А1. Таким образом, на каждой стороне АА1 квадрата отмечали точки В и В1, для которых выполняются пропорции
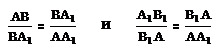Затем каждую точку А (или А1) соединяли с противолежащими точками В (или В1). Получались четыре полосы, в пересечении которых образовались два квадрата. Отрезки между вершинами и точками пересечения сторон малых квадратов составляли пропорциональные величины (в порядке возрастания: r, e, n, s, а).
Для канонических статуй и рельефов максимальный разрез фигуры соответствовал стороне m большого квадрата. Местоположение отдельных элементов фигуры – уровень носа, рта, шеи, плеч, пояса и т. д. – определялось последовательно возрастающими величинами, отмеряемыми от верхнего предела.
Достижения египтян удивляли и восхищали художников Древней Греции. Они специально совершали путешествия в Египет, чтобы поучиться умению пользоваться каноном.
Греки продолжили и развили традиции египтян в искусстве. Ставя во главу угла образ человека, они наблюдали и изучали человеческое тело во всех деталях. Греческие художники утверждали, что в мире царит всеобщая закономерность, а сущность прекрасного заключается в строгом порядке, в симметрии, в гармонии частей и целого, в правильных математических отношениях.
Одним из высших достижений греческого, да и всего мирового искусства явилось творчество афинского скульптора Фидия (V век до н. э.). Он был главным помощником Перикла при реконструкции Акрополя в Афинах. Творчество Фидия оказало влияние на ваятельное искусство всего эллинизма. Его образы, наделенные жизненной достоверностью, свидетельствуют о глубоком изучении реального мира.
Самым гармоничным отношением Фидий считал золотое сечение. Благодарная память о скульпторе до сих пор сохраняется в этом понятии, поскольку числовое значение золотого сечения обозначается через j по первой букве имени Фидия.
Золотое сечение – такое деление («сечение») данного отрезка длины a на две неравные части x и y, a = x+y, x>y, при котором меньшая часть относится к большей так же, как большая часть к целому, то есть x:y=x:a. Из этого определения следует:
или
Решая это квадратное уравнение и отбрасывая отрицательный корень, находим
» 0,62.
Полученное число и обозначается через j.
Отрезок прямой АВ можно разделить на две части следующими способами:
- на две равные части – АВ: АС= АВ: ВС;
- на две неравные части в любом отношении (такие части пропорции не образуют).
Таким образом, когда выполняется равенство АВ: АС= АС: ВС или a: b= b: c (рис. 2), это и есть золотое деление или деление отрезка в крайнем и среднем отношении.
|
Рис. 2.
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки (рис. 3).
Рис. 3.
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE=0,618..., если АВ принять за единицу, ВЕ=0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.
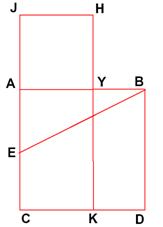
Рассмотренная задача очень древняя, она присутствует в «Началах» Евклида, который решил ее геометрически (рис. 4).
|
Рис. 4.
Рис. 4.
На отрезке АВ построен квадрат АВCD. Требуется найти точку Y, делящую АВ в среднем отношении. Соединим точку Е – середину АС – с точкой В. На продолжении стороны СА квадрата отложим отрезок ЕJ=ВЕ. На отрезке АJ построим квадрат FJHY. Продолжение стороны HY до пересечения с СD в точке К делит квадрат АВСD на два прямоугольника AYKC и YBDK. Существует чисто геометрическое доказательство, что прямоугольник YВDК равновелик квадрату AJHY.
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый (рис. 5).
|
Рис. 5.
Из подобия треугольников АСD и АВЕ можем вывести уже известную пропорцию:
|
Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться. Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
Пентаграмму никто не изобретал, ее только скопировали с натуры. Вид пятиконечной звезды имеют пяти лепестковые цветы плодовых деревьев и кустарников, морские звезды. Те и другие создания природы человек наблюдает уже тысячи лет. Поэтому естественно предположить, что геометрический образ этих объектов – пентаграмма – стала известна раньше, чем «золотая пропорция».
Портрет Монны Лизы (Джоконды) долгие годы привлекал внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника (рис. 6).
Рис. 6.
В работах скульптора Фидия (Афина Парфенос, Аполлон Бельведерский, Зевс Олимпийский – рис. 7) золотое сечение заложено в различных пропорциях человеческого тела. Не только вся статуя, но и отдельные ее части делятся в золотом отношении.
Рис. 7.
«Божественную пропорцию» также использовали зодчие при возведении величественных греческих храмов. Отношение высоты здания Парфенона в Афинах (рис. 8) к его длине равно j. Если выполнить деление высоты Парфенона по золотому сечению, получим те или иные выступы здания:
=j
Рис. 8.
В особый вид изобразительного искусства Древней Греции следует выделить изготовление и роспись всевозможных сосудов. В изящной форме амфор и кратеров, а также в их росписи легко угадываются пропорции золотого сечения. Например, амфора на рис. 9, бвыдержана в следующих пропорциях:
=j.
Рис. 9, б.
В эпоху средневековья достижения античного искусства были преданы забвению. Художники этого времени не знали принципов построения фигур, которыми пользовались великие мастера древности. Безвозвратно погибли драгоценные рукописи, в которых содержались теория и математические выкладки по композиции и рисунку великих мастеров. Многие прославленные произведения искусства, которые могли служить образцами, были уничтожены. Начиная со времен императоров Рима и до блистательной эпохи Возрождения, изобразительное искусство существовало отдельно от науки. За короткий срок были забыты традиции реализма, рисунок стал условным и схематическим. На миниатюрах XII века мы видим изображение человека с нарушением всех пропорций человеческой фигуры. Герои рисунков имеют большеголовые тела и огромные руки и ноги (рис. 10).
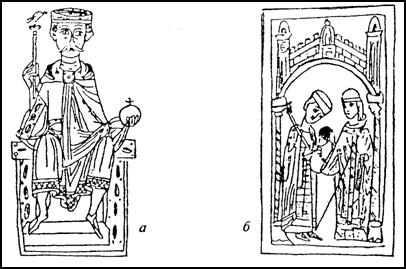
Рис. 10.
Потеряв знания о математических соразмерностях фигур, художники потеряли и изобразительную силу искусства. Чтобы возродить былые реалистические традиции, нужно было начинать все сначала. Это выпало на долю художников эпохи Возрождения.
Применение золотого сечения, для определения зрительного центра.
При изображении объектов на картине важно правильно их расположить. На первый взгляд было бы расположить объект по середине, но это не так. Наиболее гармоничными смотрятся объекты, расположенными согласно золотому сечению. Часто используются четыре точки, расположенные на расстоянии 3/8 и 5/8 от соответствующих краёв плоскости.
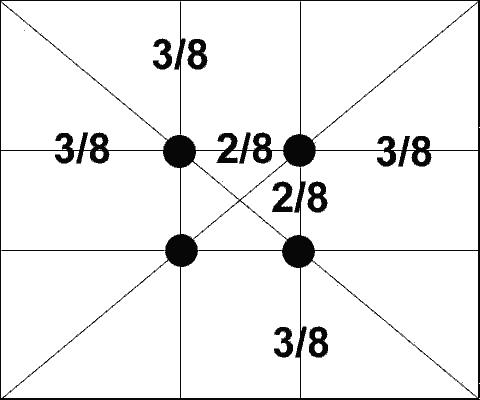
Примером использования данного приёма является картина «Утро в сосновом лесу».