На знаменитой картине «Корабельная роща» (рис. 28) с очевидностью просматриваются мотивы золотого сечения.
|
Рис. 28.
Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны – освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали (рис. 29).
|
Рис. 29.
Для наибольшей наглядности представим схематически картину следующим образом (рис. 30).
Рис.30.
Здесь линия ВК соответствует главной сосне, DТ – верхнему краю пригорка; пунктирная линия ОР – первой сосне в левой части картины…
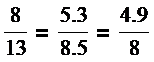= j » 0,62.
Слева от главной сосны находится множество сосен – при желании можно с успехом продолжить деление картины по золотому сечению и дальше.
Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придают ей характер уравновешенности и спокойствия, в соответствии с замыслом художника.
Когда же замысел художника иной, если, скажем, он создает картину с бурно развивающимися действиями, подобная геометрическая схема (с преобладанием вертикалей и горизонталей) становится неприемлемой.
IV. Заключение
В данной работе рассмотрено только несколько законов математики, применяемых живописцами. Но этого уже достаточно, чтобы убедиться во взаимосвязи двух на первый взгляд несовместимых понятий: математика и живопись.
Преподавание в школе предметов математики и изобразительного искусства будет считаться недостаточно глубоким, если не будет раскрыто практическое их применение в повседневной жизни. Глубокие изменения в экономике и технике в 20 веке привели к возникновению новой науки, получившей название технической эстетики или дизайна, а, следовательно, и новой профессии – художника-конструктора. Основываясь на расчетах, используя геометрические законы, применяя математические методы, компьютерную графику и художники, и дизайнеры создают для нас такие произведения искусств, которые улучшают эмоциональное и психологическое состояние человека, повышают его работоспособность.
Изложенный выше материал поможет учителям использовать его не только на уроках, но и на внеклассных мероприятиях в целях повышения интереса учащихся к изучению данных предметов, расширения кругозора детей.
Учащиеся смогут понять, что математика не только «ум в порядок приводит», но и несет в себе большой эстетический потенциал в развитии различных видов искусства, являясь «царицей всех наук».
Литература
1) и др. Что такое. Кто такой. – М.: «Педагогика-Пресс», 1996. – Т. 2, – с. 416.
2) и др. Что такое. Кто такой. – М.: «Педагогика-Пресс», 1996. – Т. 3, – с. 336.
3) Геометрия. // Учебник для 10-11 классов средней школы. / Изд. 2-е.– М.: «Просвещение», 1993. – с. 206.
4) Занимательное черчение. // Пособие для учащихся. / Изд. 3-е. – М.: «Просвещение», 1977. – с. 191.
5) Эстетика урока математики // Пособие для учителей. – М.: «Просвещение», 1981. – с. 25.
6) XX век. Сам о себе. Персоналии и течения. Малевич // Искусство. Приложение к газете «Первое сентября». – М., 2001. – № 1. – С. 1-3.
7) XX век. Сам о себе. Персоналии и течения. У истоков кубизма. Искусство. Приложение к газете «Первое сентября». – М., 2001. – № 7. – С. 5-8.
8) Толковый словарь русского языка / Изд. 2-е. – М.: «АЗЪ», 1994. – с. 907.
9) Золотая спираль. // Квант. Научно-популярный физико-математический журнал АН СССР и АПН СССР. – М.: «Наука», 1984. – № 9. – С. 15-17.
10) Леонардо да Винчи. // Математика. Приложение к газете «Первое сентября». – М., 2003. – № 4. – С. 7-10.
11) Присутствие красоты. // Математика в школе. Научно-теоретический и методический журнал МО РФ. – М.: «Школьная пресса», 2001. – № 3. – С. 73-75.
12) Наглядная геометрия. 5-6 классы // Пособие для общеобразовательных учебных заведений. / Изд. 4-е. – М.: «Дрофа», 2001. – с. 192.
13) О золотом сечении и не только о нем. // Математика в школе. Научно-теоретический и методический журнал МО РФ. – М.: «Школьная пресса», 2001. – № 3. – С. 75-76.