Рассмотрим сходящийся ряд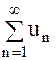 
. Как было отмечено ранее, вычисление его суммы 
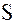непосредственно по определению очень неудобно, однако для достаточно больших n имеет место приближенное равенство 
, точность которого возрастает с увеличением n. Для оценки точности этого приближенного равенства введем понятие остатка сходящегося ряда.
Определение. Разность между суммой 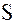и n -й частичной суммой 
ряда называется n -м остатком сходящегося ряда: 
.
Очевидно 
, т. е.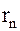 
представляет собой сумму сходящегося ряда, который получен из данного 
исключением первых n членов. Так как по определению 
, то
.
Абсолютная погрешность при замене 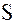частичной суммой равна 
. Таким образом, если требуется найти сумму ряда с точностью до
, то надо взять столько первых членов ряда, чтобы выполнялось условие
. Однако, отметим еще раз, остаток 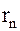– также сумма ряда, и находить его мы в большинстве случаев не умеем. Поэтому выясним, как найти номер ос
татка n, чтобы , т. е. как произвести только оценку остатка, не находя его самого. Это позволит нам вовремя остановиться при вычислении частичных сумм ряда, когда уже будет получено приближение требуемой точности.
Не формулируя теорем об оценке остатка, отметим следующие вполне очевидные факты:
1) если 
и 
– сходящиеся знакоположительные ряды и
то 
, где 
, 
;
2) если знакочередующийся ряд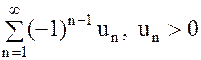 
, сходится по признаку Лейбница, то 
, т. е. абсолютная величина остатка такого ряда меньше модуля первого отброшенного члена ряда. (Это следует из того, что по теореме Лейбница сумма ряда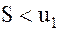 
).
Если данный ряд знакоположительный, то его остаток 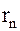, составленный из отброшенных членов, чаще всего сравнивают с бесконечно убывающей геометрической прогрессией, т. к. ее сумма вычисляется по известной формуле 
.
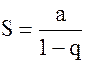Пример 11. Вычислить сумму ряда с точностью 
, если
| а) |  ;
| б) |  .
|
Решение. а) 
– ряд геометрической
прогрессии со знаменателем 
.
По определению 
является также рядом геометрической прогрессии с и первым членом 
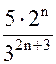. Найдем сумму этой прогрессии, т. е. :
.
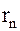Путем подбора определим, при каком значении n будет выполняться неравенство 
. Положим, например, 
. Получим 
, т. е.
. Так как 
, то три слагаемых не дают приближение
требуемой точности. Пусть 
, отсюда 
, т. е. 
.
Итак, принимаем . Это означает, что
с точностью .
Неравенство 
можно было решить и не прибегая к подбору:
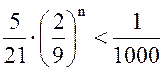, поэтому 
или 
.
Приближенное значение полученной дроби можно вычислить на калькуляторе.
б) Знакоположительный ряд 
геометрической прогрессией не является, но при всех 
справедливо неравенство: 
.
– ряд геометрической прогрессии со знаменателем
. Очевидно, , где 
– n -й остаток исследуемого ряда, а
.
Поэтому 
.
Так как 
, то 
. Значит, 
также меньше 
и
с заданной точностью .
Пример 12. Вычислить сумму ряда с заданной точностью:
| а) |  ,
|  ;
| б) |  ,
| ;
|
| в) |  ,
|  ;
| г) |  ,
| .
|
а) Ряд 
сходится по признаку Лейбница. Сумма n первых
членов этого ряда 
отличается от его суммы
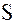на величину меньшую, чем 
. Поэтому, отбросив десятый и следующие за ним члены, получим 
с точностью .
б) Для того, чтобы вычислить приближенно сумму ряда 
с такой же точностью , придется взять не 9, как в примере а), а 99
первых слагаемых, т. к. 
и 
.
Сравнение результатов, полученных в примерах а) и б), приводит к понятию скорости сходимости рядов: очевидно, ряд 
сходится быстрее, чем , т. к. для вычисления суммы с одной и той же точностью в первом случае необходимо взять меньше слагаемых, чем во втором.
в) Знакочередующийся ряд 
удовлетворяет условиям признака Лейбница, а поэтому допускаемая погрешность 
. 
, значит,
с заданной точностью .
г) Данный ряд также сходится по признаку Лейбница. Абсолютная величина
его седьмого члена 
, следовательно, частичная сумма 
отличается от суммы ряда менее, чем на , и
.