Существует три формы комплексного числа, так как различные операции над комплексными числами удобнее проводить с различными формами.
1. Алгебраическая форма: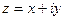 
.
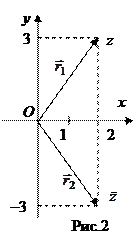
Пример 1. Найти действительную и мнимую части, модуль, аргумент комплексного числа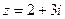 
, сопряженное к нему и изобразить 
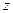и 
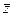на комплексной плоскости.
Решение.
Действительная и мнимая части: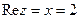 
, 
.
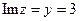Модуль: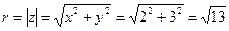 
.
Аргумент: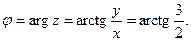 
Сопряженное к z равно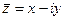 
, тогда, если 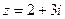, то сопряженное к нему равно 
.
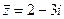Комплексному числу 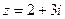соответствует вектор 
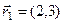, комплексному числу 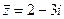соответствует вектор 
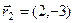, z и 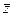изображены на рис.2.
2. Тригонометрическая форма: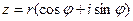 
.
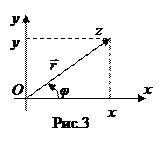Из рисунка 3 видно, что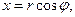 
.
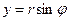Если подставить данные выражения в алгебраическую форму, то получится комплексное число в тригонометрической форме:
= 
.
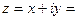
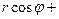
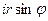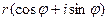Пример 2. Представить в алгебраической форме комплексное число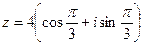 
. Найти к нему сопряженное.
Решение.
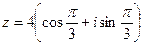, отсюда 
.
.
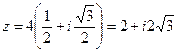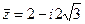3. Показательная форма: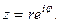 
Используя формулу Эйлера
,
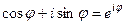комплексное число 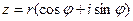можно записать в так называемой показательной форме:
z =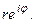 
Пример 3. Представить в показательной форме комплексное число 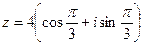. Записать к нему сопряженное, найти модуль.
Решение.
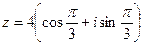, отсюда 
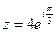, тогда 
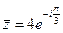, r = 4.
Пример 4. Дано комплексное число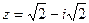 
. Записать его в трех формах.
 |
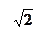
Решение.
 | |||
 |
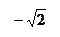
Рис.4
Алгебраическая форма комплексного числа: .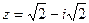
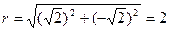, если главное значение аргумента определяется промежутком 
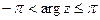(поворот по часовой стрелке), то 
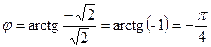, тогда тригонометрическая форма комплексного числа запишется так:
.
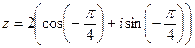Если главное значение определяется промежутком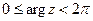 
, то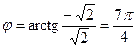 
(угол на рисунке обозначен мелким штрихом, поворот против часовой стрелки, рис.4), тогда тригонометрическая форма комплексного числа запишется так:
.
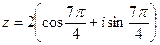Показательная форма комплексного числа: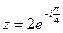 
или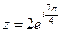 
.
Действия над комплексными числами
Сложение.
Суммой двух комплексных чисел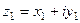 
и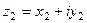 
называется комплексное число, определяемое равенством:
.
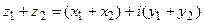Пример 6. (1 + i) + (–2 + 3 i) = (1– 2) + i (1 + 3) = –1 + 4 i.
Вычитание.
Вычитание определяется как действие, обратное к сложению:
Разностью двух чисел 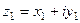и 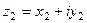называется число 
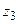такое, что сумма 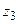и 
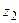равна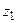 
, т.е. 
: 
.
.
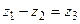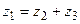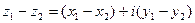Умножение.
Умножение производится над комплексными числами во всех формах: алгебраической, тригонометрической, показательной:
,
,
.
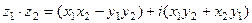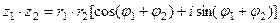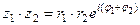Замечание. Доказательство данных формул следует из определения мнимой единицы и правил умножения, а также тригонометрических формул.
Пример 7. Перемножить комплексные числа:
1) (1 + i) · (–2 + 3 i) = (по определению) = (1· (– 2) – 1· 3) + i (1 · 3 + 1 · (–2)) = –5 + i.
(1 + i) · (–2 + 3 i) = (перемножаем как многочлены) = – 2 + 3 i –2 i +i · 3 i = –2 + i – 3= = –5 + i.
Пример 8. Получить значения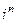 
, где n – натуральное число.
Решение.
, 
, 
, 
, 
, 
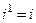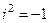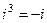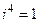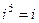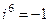и т.д.,
Прослеживается закономерность: результат повторяется через четыре действия. Зная это, легко можно найти значение i в любой степени, например,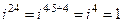 
.
Замечание. 
Деление.
Операция деления вводится как обратная к операции умножения: частным двух чисел 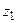и 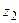называется число 
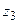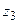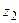такое, что произведение и равно 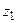, т.е. 
.
.
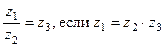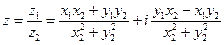На практике частное двух комплексных чисел, заданных в алгебраической форме, находят путем умножения и числителя и знаменателя на число, сопряженное знаменателю («избавляются от мнимости в знаменателе»):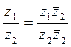 
.
Пример 9. Найти частное двух комплексных чисел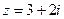 
и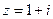 
.
Решение.
.
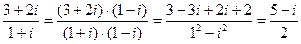Деление в тригонометрической форме: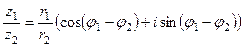 
.
Деление в показательной форме: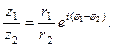 
Возведение в степень.
Возведение в степень удобнее производить над комплексными числами в тригонометрической и показательной формах:
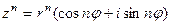– формула Муавра,
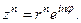
Замечание. Формула Муавра следует из перемножения комплексных чисел, записанных в тригонометрической форме.
Пример 10. Возвести в шестую степень комплексное число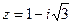 
.
Решение.
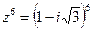, в данном случае для нахождения значения выражения удобнее представить число 
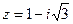в тригонометрической форме: 
, 
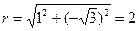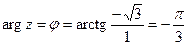, тогда
= 
. 
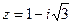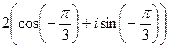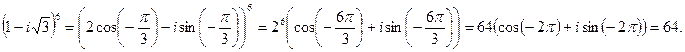
Извлечение корня.
Извлечение корня удобнее производить над комплексными числами в показательной и тригонометрической формах.
Определение 10. Корнем n – ой степени из комплексного числа z,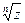 
, называется число W такое, что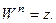 
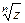– многозначная функция (имеет несколько значений, в зависимости от n), в связи с чем записывается: 
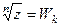, где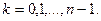 
Значение 
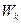можно найти в тригонометрической или показательной формах:
.
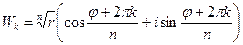Все значения корня 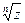располагаются на окружности, радиус которой 
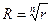, а точки, соответствующие комплексным числам – корням Wk, делят окружность на n равных частей.
Пример 11. Вычислить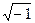 
.
Решение.
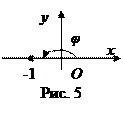1 способ. Представим число z = –1 в тригонометрической форме. Для этого изобразим его на плоскости (рис. 5). Из рисунка видно, что
r = 1, φ = π. (можно было найти по формулам)
Тогда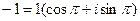 
.
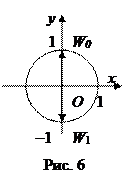Корень степени n = 2, отсюда k = 0, 1.
Подставим в формулу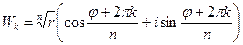 
:
при k = 0: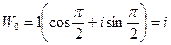 
;
при k = 1: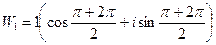 
.
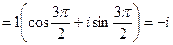Изобразим корни на окружности радиуса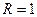 
(рис. 10).
2 способ. Представим число z = –1 в показательной форме: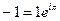 
.
При k = 0: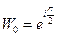 
, при k = 1: 
.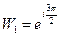