ГрафомG называют пару множеств (V, E), где V – множество вершин графа(точек); E – семейство ребер графа(отрезков или дуг, соединяющих вершины в пары):
V ={ v 1, v 2, v 3,…, vn };
E ={ e 1, e 2, e 3,…, em };
ei =(v J,v K) – i -е ребро графа G; vJ, vK – концевые вершины этого ребра (i =1,2,3,…, m; vj, k =1,2,…, n).
Если концевые вершины ребра совпадают, то ребро образует петлю (дугу, начало и конец которой совпадают).
Пример графа на четырех вершинах, имеющего восемь ребер, одно из которых – петля (e 8), приведен на рис. 17. Ребра e 4, e 5 кратные или параллельные друг другу, так же как и ребра e 6 и e 7.

Ребра графа могут быть ориентированными или неориентированными. Граф на рис. 4 имеет неориентированные ребра. Если все ребра графа ориентированы, то граф называют ориентированными графами или орграфами.
Если вершины vi и vj (i ≠ j) соединены ребром ek = (vi, vj), то их называют смежными вершинами. Если ребра ek, el имеют общую вершину, то их называют смежными ребрами. Если вершина vi является концом ребра ej , то vi называют вершиной, инцидентной ребру ej, а ej – ребром, инцидентным вершине vi.
Термин “ степень вершиныграфа ” является числовой
характеристикой каждой из его вершин.
Степень вершины – это число ребер, инцидентных данной вершине, причем петли учитываются дважды.
Степень вершины v обозначают символом r(v).
Если степень вершины графа равна нулю, то вершину называют изолированной вершиной.
Степень вершины можно подсчитать по числу концов ребер, входящих в эту вершину или выходящих из нее. Поскольку петля и входит в вершину и выходит из нее, ее вклад в степень вершины равен двум. Каждое ребро, не являющееся петлей, вносит вклад в степень ровно двух вершин графа. Следовательно, удвоенное число ребер равно сумме степеней его вершин:
 , ,
| (1) |
где n – число вершин графа, m – число его ребер.
Граф считают заданным, если известны его вершины, ребра и соответствие инцидентности между множествами вершин и ребер. Наряду с геометрическим изображением графа, используют задание его с помощью матриц.
Матрица смежности графа, построенного на n вершинах, представляет собой матрицу, порядка n: A = [ aij ] nxn, где aij – это число ребер, соединяющих вершины vi и vj, причем петли, “соединяющие” вершину с самой собой, считаются дважды.
Матрица инциденций графа на n вершинах, имеющего m ребер, – это матрица I =[ bij ] n´m, состоящая из n строк и m столбцов.
Если граф ориентированный, тогда:
bij = 1, если ребро ej выходит из вершины vi;
bij = –1, если ребро ej входит в вершину vi,;
bij = 0, если ребро ej неинцидентно вершине vi или является петлей при этой вершине.
Если граф неориентирован, тогда:
bij = 1, если ребро ej инцидентно вершине vi и не является ее петлей;
bij = 2, если ej – петля при вершине vi;
bij = 0, если ребро ej неинцидентно вершине vi.
Пример.
Граф G задан матрицей инциденций:
| e 1 | e 2 | e 3 | e 4 | e 5 | e 6 | e 7 | |
| v 1 | |||||||
| v 2 | |||||||
| v 3 | |||||||
| v 4 | |||||||
| v 5 | |||||||
| v 6 |
Требуется:
1) построить граф;
2) найти степень каждой из его вершин;
3) записать матрицу смежности графа.
Р е ш е н и е.
1)
 |
2) Число степеней вершин графа проще всего найти, сложив числа в каждой из строк матрицы инциденций:
| e 1 | e 2 | e 3 | e 4 | e 5 | e 6 | e 7 | 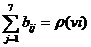
| |
| v 1 | ||||||||
| v 2 | ||||||||
| v 3 | ||||||||
| v 4 | ||||||||
| v 5 | ||||||||
| v 6 |
3) Матрица смежности графа G:
| v 1 | v 2 | v 3 | v 4 | v 5 | v 6 | |
| v 1 | ||||||
| v 2 | ||||||
| v 3 | ||||||
| v 4 | ||||||
| v 5 | ||||||
| v 6 |
Разрезы и циклы графа
Определим еще несколько терминов теории графов.
Простой граф – это граф, не содержащий петель и кратных ребер.
Полным графом называют простой граф, в котором любые две вершины смежны. Обозначают полный граф на n вершинах символом Kn.
Двудольным графом называют простой граф, у которого множество вершин распадается на два непересекающихся подмножества V 1 и V 2, причем никакие две вершины из V 1 несмежны друг другу и никакие две вершины из v 2 также несмежны друг другу. Если каждая вершина из V 1 смежна всем вершинам из V 2, то граф называют полным двудольным графом. Обозначают полный двудольный граф символом Km , n , где m – число вершин во множестве V 1, а n – число вершин во множестве V 2.
Маршрут – это последовательность вершин и ребер графа, следуя по которым, можно попасть из одной его вершины в другую.
Цепь – это маршрут без повторяющихся ребер.
Путь – это цепь, все вершины которой (за исключением быть может начальной и конечной) различны.
Цикл – это цепь у которой совпадают начальная и конечная вершины, а все остальные различны.
Очевидно, что четыре последних понятия находятся в следующем соотношении: пути и циклы – это особые виды цепей, цепь – особый вид маршрута. Понятие маршрута в теории графов очень близко к обыденному понятию маршрута.
Граф называют связным, если из каждой его вершины существует путь в любую другую его вершину.
Очевидно, что полный граф является связным: в нем существуют все возможные пути между любыми двумя его вершинами.
Рассмотрим полный граф К 4 , а также некоторые его подграфы, полученные путем последовательного исключения ребер (рис. 22).
 |
Подграфы G 1 и G 2 остаются связными, в подграфе G 3 связность нарушается: граф распадается на компоненты – изолированную вершину и К 3. Если в подграфе G 2 убрать другое ребро, граф останется связным (G 4), однако степень его связности значительно ниже, чем в К 4: для нарушения связности К 4 пришлось вынуть из него 3 ребра, для нарушения связности G 4 достаточно удалить одно из трех его ребер.
Множество ребер, которые нужно удалить из связного графа, чтобы он перестал быть связным, называют разрезающим множеством. Пусть V 1 и V 2 – два непересекающихся подмножества множества вершин связного графа G =(V, E). Разрезом графа G называют разрезающее множество, разделяющее граф на компоненты G 1= = (V 1, E 1) и G 2 = (V 2, E 2).
Отметим, что в ориентированном графе выбирается направление разреза, например, от множества V 1 к множеству V 2 или наоборот. Направление ребер разреза либо совпадает с выбранным направлением, либо противоположно ему. В неориентированном графе направление ребер не выбирается.
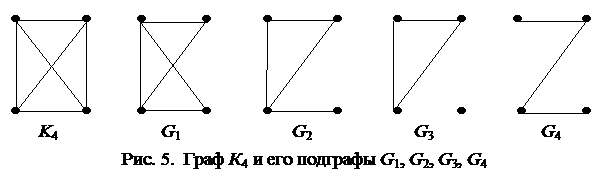
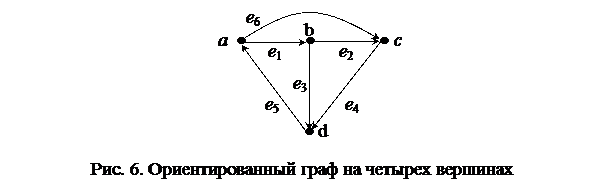
Рассмотрим несколько разрезов графа, изображенного на рис. 6 (направление разреза выбирается произвольно).
 |
1. V 1={ a }, V 2={ b, c, d }:
 |
2. V 1 = { b }, V 2 = { a, c, d }:
 |
3. V 1 = { a, b }, V 2 = { c, d }.
 |
Матрицей разрезов графа называют матрицу Q =  k ´ m , где k – число всех разрезов графа, m – число его ребер.
k ´ m , где k – число всех разрезов графа, m – число его ребер.
Причем для орграфа:
qij = 1, если ребро ej Î Ri и его направление совпадает с направлением разреза Ri;
qij = –1, если ребро ej Î Ri и его направление противоположно направлению разреза Ri;
qij = 0, если ребро ej Ï Ri.
Для неориентированного графа:
qij = 1, если ребро ej Î Ri;
qij = 0, если ребро ej Ï Ri (i = 1, 2,…, k; j = 1, 2,…, m).
Во многих практически важных задачах, использующих графы, возникает необходимость найти все разрезы графа. Например, при анализе электрических цепей, анализе сетей и пр.
Составим несколько строк матрицы разрезов, рассмотренных в приведенном выше примере:
| e 1 | e 2 | e 3 | e 4 | E 5 | E 6 | ||
| Q = | R 1 | –1 | –1 | ||||
| R 2 R 3 ¼ | ¼ | –1 ¼ | –1 ¼ | ¼ | –1 ¼ | ¼ |
Подчеркнем, что составление матрицы Q осталось незаконченным, существует еще несколько разрезов, которые должны дать новые строки в матрице Q.
Строки матрицы разрезов можно рассматривать как двоичные векторы линейного пространства над полем B ={0,1}, имеющее определенный базис. Двоичные векторы можно умножать на число из поля B, складывать по модулю 2, находить их скалярное произведение.
Наряду с разрезами, большое значение в прикладных задачах имеют циклы графа. Для записи циклов графа используется матрица циклов, или цикломатическая матрица. Составляется эта матрица аналогично матрице разрезов. В орграфе предварительно выбирается направление обхода цикла.
Пусть В = 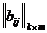 – цикломатическая матрица графа G. Здесь k – число всех циклов G, m – число его ребер. Причем для орграфа:
– цикломатическая матрица графа G. Здесь k – число всех циклов G, m – число его ребер. Причем для орграфа:
bij = 1, если ej Î Ci (i -му циклу графа G) и направление ребра совпадает с направлением обхода цикла Ci;
bij = –1, если ej Î Ci и направление ребра ej противоположно направлению обхода цикла;
bij = 0, если ej Ï Ci .
Для неориентированного графа:
bij = 1, если ej Î Ci;
bij = 0, если ej Ï Ci (i = 1, 2,…, k; j = 1, 2,…, m).
Запишем несколько строк матрицы циклов графа, представленного на рис. 6:
С 1 = { e 1, e 3, e 5};
C 2 = { e 2, e 4, e 3};
C 3 = { e 1, e 2, e 4, e 5}.
| e 1 | е 2 | е 3 | е 4 | е 5 | е 6 | ||
| В = | С 1 | ||||||
| С 2 | –1 | ||||||
| С 3 | |||||||
| ... | ... | ... | ... | ... | .. |
Строки цикломатической матрицы, как и строки матрицы разрезов, можно рассматривать как двоичные векторы линейного пространства над полем B ={0,1}, в котором можно выделить систему базисных векторов.
Граф, не содержащий ни одного цикла, называют ациклическим графом.
 Деревом называют связный ациклический граф (рис. 7)
Деревом называют связный ациклический граф (рис. 7)
Деревом графаG называют связный ациклический подграф графа G (рис. 8, а).
Остов графаG – это дерево Т графа G, содержащее все вершины графа G (рис. 8, б).
Коостов T * остова T графа G – это подграф графа G, содержащий все его вершины и только те ребра графа, которые не входят в Т (рис. 25, в). Отметим, что T * может быть несвязным графом.

Ребра остова T называют ветвями остова, а ребра соответствующего коостова T * называют хордами или связками остоваТ.
В дальнейшем нам используются следующие, достаточно очевидные утверждения относительно деревьев:
Утверждение 1. Если граф G является деревом, то существует только один путь между любыми двумя его вершинами.
Утверждение 2. Если граф G связный, и число его ребер на единицу меньше числа его вершин (m = n –1), то G – дерево.
Утверждение 3. Если G – ациклический граф и при соединении двух его несмежных вершин образуется ровно один цикл, то граф G – дерево.
Приведем также несколько утверждений относительно остовов графа.
Утверждение 4. Подграф T графа G является остовом G тогда и только тогда, когда T ацикличен и число его ребер на единицу меньше числа вершин графа G.
Утверждение 5. Граф G является связным тогда и только тогда, когда он имеет остов.
Любой остов графа G порождает базисную систему циклов графа G и базисную систему разрезов этого графа.
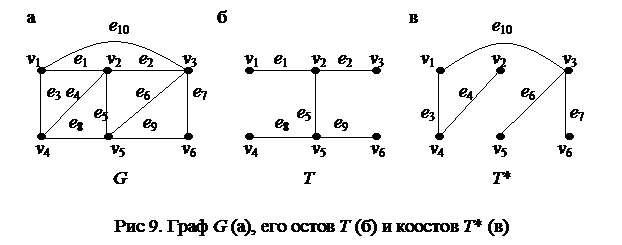
Пусть G – связный граф и T – какой-либо из остовов этого графа (рис. 9). Если дополнить остов Т каким-либо ребром графа G, не входящим в остов, образуется ровно один цикл (см. утверждение 3) графа G. Перебирая все хорды дерева Т (иными словами, все ребра коостова Т* или все ребра графа G, не вошедшие в T), получим систему циклов графа, которую называют базисной системой циклов графа G относительно остова T.
 | ||
 |
Рис. 9 и 10 иллюстрируют получение базисной системы циклов графа G относительно выбранного остова.
Запишем цикломатическую матрицу системы базисных циклов графа G, при этом необходимо учесть следующее:
1) выбор остова Т разбивает множество Е ребер графа на два непересекающихся подмножества: множество хорд остова Т (множество ребер коостова) и множество ветвей остова Т (множество ребер самого остова);
2) каждая хорда порождает один и только один базисный цикл.
В базисной цикломатической матрице первые столбцы соответствуют хордам, за ними идут столбцы, соответствующие ветвям. Число строк матрицы (число базисных циклов) равно числу хорд.
Матрица базисных циклов для графа на рис. 9:
| Хорды остова Т | Ветви остова Т | ||||||||||
| e 3 | e 4 | e 6 | e 7 | e 10 | e 1 | e 2 | e 5 | e 8 | e 9 | ||
| Bf = | Cf 1 | ||||||||||
| Cf 2 | |||||||||||
| Cf 3 | |||||||||||
| Cf 4 | |||||||||||
| Cf 5 | |||||||||||
| U | BfT |
Базисная цикломатическая матрица Bf графа G распадается на две подматрицы: U – единичную матрицу, соответствующую хордам остова Т, порождающим базисные циклы, BfT – матрицу, соответствующую ветвям остова Т, называемую фундаментальной цикломатической матрицей графаG по остову T.
Пусть связный граф G имеет n вершин и m ребер. Согласно утверждению 4, любой остов T такого графа содержит n –1 ребро, и, следовательно, соответствующий ему коостов T * содержит k = m –(n– 1) ребер. Учитывая, что каждое ребро Т * порождает базисный цикл, можно утверждать, что любая система базисных циклов графа состоит из k = m – n+1 циклов.
Таким образом, любая базисная цикломатическая матрица графа G – это матрица размерности k ´ m. Она состоит из двух подматриц: единичной матрицы порядка k и фундаментальной цикломатической матрицы графа G по остову T, которая имеет размерность k ´(n –1).
| Bf = [ U ½ BfT ], | (2) |
где Bf – базисная цикломатическая матрица графа G по остову Т размерностью k ´ m (k = m–n +1); U – единичная матрица порядка k, соответствующая хордам остова Т; BfT – фундаментальная цикломатическая матрица графа G по остову T размерностью k ´(n –1), соответствующая ветвям остова Т.
Найдем базисную систему разрезов, базисную матрицу разрезови фундаментальную матрицу разрезов графа G по остову T. Заметим, что если изъять одну из ветвей остова Т, то остов распадется на две компоненты, при этом множество вершин графа окажется разбитым на два непересекающихся подмножества T 1 и Т 2. Разрез графа, соответствующий такому разбиению, является одним из искомых базисных разрезов. Проделывая аналогичную процедуру для каждой из ветвей остова Т, получим всю систему базисных разрезов графа. Поскольку число ветвей любого остова на единицу меньше числа вершин графа и каждая ветвь дает один базисный разрез, то число базисных разрезов по любому остову равно n –1, где n – число вершин графа.
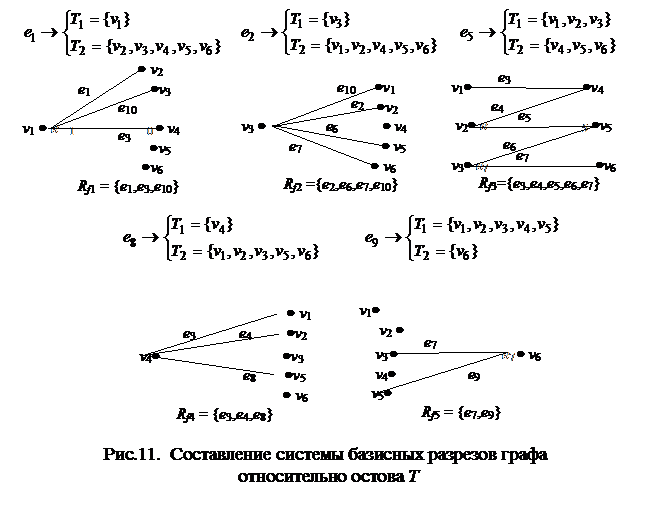
Матрица базисных разрезов графа относительно дерева Т распадается на две подматрицы: QfT – матрицу размерностью (n – 1)´k, (k=m – n+1), соответствующую хордам остова Т (или фундаментальной
На рис. 11 показана процедура составления системы базисных разрезов графа G по остову Т, изображенных на рис. 9.
Запишем матрицу полученной системы базисных разрезов:
| Хорды остова Т | Ветви остова Т | ||||||||||
| e3 | e4 | e6 | e7 | e10 | e1 | e2 | e5 | e8 | e9 | ||
| Qf = | Rf1 | ||||||||||
| Rf2 | |||||||||||
| Rf3 | |||||||||||
| Rf4 | |||||||||||
| Rf5 | |||||||||||
| QfT | U |
Базисная матрица разрезов Qf графа G распадается на две подматрицы: U – единичную матрицу, соответствующую ветвям остова Т, порождающим базисные разрезы, QfT – матрицу, соответствующую хордам остова Т, называемую фундаментальной матрицей разрезов графаG по остову T.
| Q f = [ QfT ½ U ]. | (3) |
Справедливо следующее утверждение.
Утверждение 6. Любая строка матрицы циклов графа G ортогональна любой строке матрицы его разрезов.
Из утверждения 6 следует равенство:
| Q×Bt = B×Qt = 0, | (4) |
где B и Q – матрицы циклов и разрезов, Qt и Bt – транспонированные матрицы разрезов и циклов.
Равенство (4) справедливо как для ориентированного, так и для неориентированного графов.
Для матриц базисных циклов и разрезов равенство (4) можно переписать в следующем виде:
· для не ориентированного графа
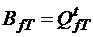 , ,
| (5) |
· для орграфа
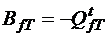 . .
|
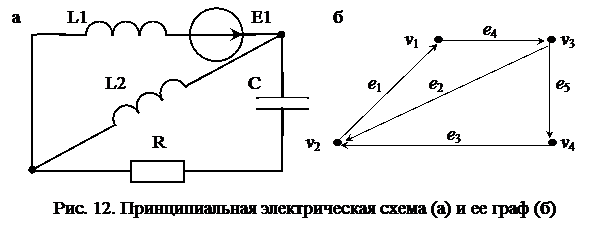
Одним из методов расчета электрических цепей является их анализ с помощью графа цепи. Элементы цепи (сопротивления, конденсаторы, катушки индуктивности и др.) соответствуют ребрам графа, узлы цепи (точки соединения элементов) – вершинам графа. На рис. 12 изображена электрическая цепь и ее граф.
Пусть граф цепи имеет m ребер. Представим токи, протекающие в элементах цепи, и напряжения на них в виде столбцов:
I=  , V = , V = 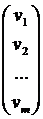 . .
| (6) |
Законы Кирхгофа для токов и напряжений могут быть записаны в виде следующих равенств:
| Q·I=0, | (7) |
| B·V=0, | (8) |
где Q и B – матрицы разрезов и циклов графа цепи.
Пусть Qf=[QfT|U] и Bf=[U|BfT], где Qf и Bf – матрицы базисных разрезов и циклов по какому-либо остову Т графа цепи. Запишем столбцы I и V в порядке, соответсвующем порядку расположения ребер в матрицах Qf и Bf. При этом столбцы I и V примут следующий вид:
I = 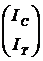 , V =
, V = 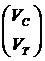 ,
,
где IC и VC – токи и напряжения в хордах дерева, IT и VT – токи и напряжения в ветвях дерева.
Тогда
[QfT½U]×  = 0, [U½BfT ]×
= 0, [U½BfT ]× 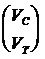 = 0.
= 0.
Учитывая равенство (7), получаем
[QfT½U]×  = [QfT×IC½IT] = 0 Þ IT = – QfT×IC =
= [QfT×IC½IT] = 0 Þ IT = – QfT×IC = 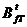 ×IC.
×IC.
Таким образом, вектор-столбец токов в цепи можно представить в виде
I=  = =  ×IC = B ×IC = B 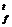 ×IC. ×IC.
| (9) |
Аналогично напряжения на элементах цепи можно представить в виде
V= 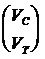 = Q = Q 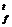 ×VT. ×VT.
| (10) |
Равенства (9) и (10) означают следующее:
1) все токи, текущие через элементы электрической цепи, представляют собой алгебраические суммы хордовых токов какого-либо остова графа цепи;
2) все напряжения на элементах электрической цепи представляют собой алгебраические суммы напряжений на ветвях какого-либо остова графа цепи.
Пример.
Дана схема электрической цепи.

Требуется:
1) построить граф цепи; а также какой-либо остов и соответствующий коостов графа;
2) записать базисные матрицы циклов и разрезов по выбранному остову, проверить ортогональность векторов циклов к векторам разрезов;
3) записать соотношение между токами и соотношения между напряжениями на элементах цепи.
Р е ш е н и е
1)

2) Матрицы Bf и Qf.
| e 2 | e 5 | e 6 | e 1 | e 3 | e 4 | e 2 | e 5 | e 6 | e 1 | e 3 | e 4 | |||||
| Bf = | Cf1 | –1 | –1 | Qf = | Rf 1 | –1 | ||||||||||
| Cf2 | Rf 1 | –1 | ||||||||||||||
| Cf3 | –1 | Rf 1 | –1 | –1 |
Проверка ортогональности:
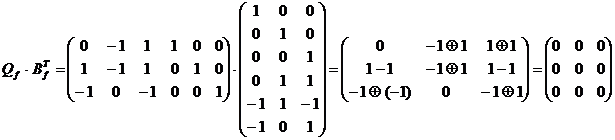

3) Соотношение между токами и напряжениями на элементах цепи:
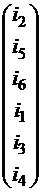 =
=  ×
× 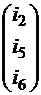 Þ
Þ 
 =
=  ×
×  Þ
Þ 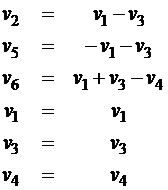
Планарные графы. Толщина графа
Граф G укладывается на поверхности S, если его можно нарисовать на этой поверхности так, чтобы его ребра пересекались только в своих концевых вершинах.
Граф называют планарным, если его можно уложить на плоскости.
Укладку графа на плоскости называют планарной укладкой.
Толщиной графаG называют наименьшее число планарных графов, объединение которых дает граф G.
Запись t(G) означает толщину графа G.
Графы, изображенные на рис. 33, называются графами Куратовского: К5 – полный граф на пяти вершинах, К3,3 – полный двудольный граф на шести вершинах (множество вершин разбито на два непересекающихся подмножества по три вершины в каждом, каждая вершина одного подмножества соединена со всеми вершинами другого подмножества). Это основные непланарные графы. Графы, содержащие в качестве подграфов непланарные графы, тоже являются непланарными.
 |
Пусть G – планарный граф, уложенный на плоскости p. Гранью графаG будем называть множество всех точек этой плоскости, которые не являются вершинами графа, не лежат на его ребрах и любые две из них можно соединить непрерывной линией, не пересекающей вершины и ребра графа.
На рис. 14 показана укладка графа на семи вершинах, имеющего 12 ребер на плоскости p. f1,f2,f3,f4,f5,f6,f7 – грани графа. Грань f7 является бесконечной гранью.
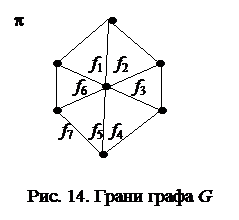 |
На рис. 15 изображены графы и указаны их грани для более сложных случаев. Грани f 4 в обоих графах бесконечны.
 |
Число вершин, ребер и граней связного планарного графа связаны простой формулой, полученной Л. Эйлером в 1752 г. и носящей его имя:
| n+f=m+2, | (11) |
где n, f и m – числа вершин, граней и ребер графа соответственно.
Из формулы Эйлера(11) вытекает неравенство, лежащее в основе критерия планарности графа: если G – связный простой планарный граф c n вершинами (n³3) и m ребрами, то
| m£ 3n – 6. | (13) |
.
Данный критерий является необходимым, но недостаточным условием планарности графа.
Проверим неравенство (13) для графов Куратовского:
K 5: n= 5, m= 10 Þ 10 £ 15–6 – ложно Þ K 5 – непланарен;
K 3,3: n= 6, m= 9 Þ 9 £1 8–6 – истинно Þ K 3,3 может быть как планарным, так и непланарным.
Докажем, что К 3,3 непланарен. Предположим противное: К 3,3 – планарен. По формуле Эйлера для связного планарного графа имеем: n+f=m+ 2 Þ f= 5. Перерисуем К 3,3 (рис. 16, а) так, как показано на рис.16, б.
 |
Видно, что все циклы К 3,3 ограничены не менее чем четырьмя ребрами, каждое ребро может разделять две грани, а следовательно, число граней этого графа f £(2×9):4, т. е. f £4 (так как f – целое число). Полученное противоречие (f =5 и f £4) говорит о том, что допущенное предположение неверно, граф К 3,3 непланарен.
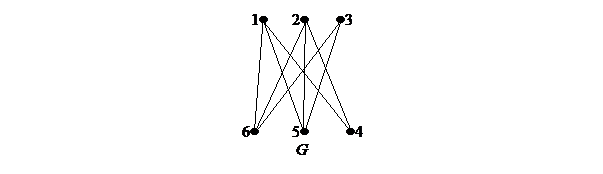 П р и м е р
П р и м е р
Дан простой граф G:
Требуется:
1) записать матрицу инциденций графа;
2) проверить выполнение необходимого условия планарности графа, найти число его граней;
выполнить чертеж графа, доказывающий его планарность, показать на чертеже все его грани.
Р е ш е н и е
1) Матрица инциденций

| 2) Число вершин графа: n=6
Число ребер графа: m=8.
По формуле Эйлера: n+f=m+2,
Следовательно:f=m-n+2=8-6+2=4
Число граней графа равно – 4.
Необходимое условие планарности графа:
 Необходимое условие выполнено, граф может быть планарен.
Необходимое условие выполнено, граф может быть планарен.
|
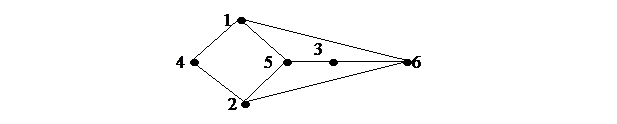 3) Расположив вершины графа в порядке, указанном ниже, убеждаемся в планарности графа.
3) Расположив вершины графа в порядке, указанном ниже, убеждаемся в планарности графа.
7. Сетевое планирование
Если каждому ребру e графа G=(V,E) поставлено в соответствие определенное число – вес ребра c(e), то G называют взвешенным графом.
Связный взвешенный орграф называют сетью.
Обозначение G = (V,E,c(e)) означает сеть, c(e) – вес или цена ребра e.
Во всех задачах, решаемых с помощью сетей, требуется найти либо минимум, либо максимум некоторой величины (кратчайший путь, максимальный поток, минимальный разрез и пр.). Минимумы или максимумы носят общее название – экстремумы. Задачи на отыскание экстремума называют задачами оптимизации.
Одной из задач дискретной оптимизации является задача сетевого планирования. Решение этой задачи позволяет составить оптимальный план выполнения задуманного проекта, а именно определить минимальное время реализации всего проекта и сроки выполнения промежуточных этапов.
Пусть требуется составить план выполнения какого-либо проекта. Обозначим работы, которые предусматриваются проектом e 1, e 2, e 3 ……, моменты окончания работ – v0, v1, v2, v3 ……, vT.
Назовем результат или завершение работы ek событием. Событие v0 – начало всех работ, vТ – их окончание. Сетевой график - это граф отношения “событие а непосредственно предшествует событию b ” на множестве событий.
Сетевой график– это сеть G ={ V, E, t (e)} с выделенной вершиной v 0, из которой ребра только выходят, и выделенной вершиной vT, в которую ребра только входят. Весь сетевой график интерпретируется как последовательность выполнения последовательности работ по осуществлению некоторого проекта.
Интерпретация элементов сетевого графика:
v0 – начало работ;
vТ – окончание работ;
E ={ e 1, e 2, …, em } – множество всех работ, необходимых для реализации проекта;
T ={ t (e1), t (e2), …, t (em)} – промежутки времени, необходимые для реализации каждой из работ;
v1, v2, …, vn – результаты выполнения работ.
Имея в виду смысловую интерпретацию сетевого графика, приходится накладывать на него требование отсутствия контуров, т. е. циклов, в которых возращение в исходную точку происходит в направлении ребер. В самом деле, наличие контуров означало бы необходимость выполнения работ с нулевым результатом: с чего начали, тем и закончили.
Ребра сетевого графика кодируются в ЭВМ как пара вершин Для того чтобы каждое ребро имело свой определенный код, граф не должен содержать параллельных ребер. В некоторых случаях это требование приводит к необходимости введения фиктивных ребер (фиктивных работ), т. е. ребер с нулевым весом. Фиктивные ребра сетевого графика обозначают штриховой линией.
Определение минимального времени реализации проекта по сетевому графику связано с отысканием в нем критического пути. К ритический путь из v0 в vT в сетевом графике – это путь, имеющий наибольший суммарный вес. Вес критического пути равен минимальному времени реализации проекта.
Если окончание работ критического пути будет задержано, то увел