Тема: Определенный интеграл (6 час.)
Цель: Вычисление определенного интеграла, нахождение площади фигур ограниченных функциями.
Инструкция:
1. Решите задачи.
2. Оформите решение задач в тетради для самостоятельных работ и сдайте преподавателю на проверку.
ЗАДАЧИ
1. Вычислить: а)  ; б)
; б)  .
.
2. Вычислить: а) 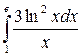 ; б)
; б)  .
.
3. Вычислить площадь криволинейной трапеции, ограниченными линиями:  .
.
4. Вычислить площадь криволинейной трапеции, ограниченными линиями:  .
.
5. Вычислить площадь фигуры, ограниченной линиями:  .
.
6. Вычислить площадь фигуры, ограниченной линиями:  .
.
Тема 3.3. Уравнения и неравенства
САМОСТОЯТЕЛЬНАЯ РАБОТА № 15
Тема: Уравнения и неравенства (8 час.)
Цель: Решение уравнений и неравенств смешанных типов применяя различные методы.
Инструкция:
1. Решите задачи.
2. Оформите решение задач в тетради для самостоятельных работ и сдайте преподавателю на проверку.
ЗАДАЧИ
1. Решите уравнение:  .
.
2. Решите уравнение:  .
.
3. Решите неравенство:  .
.
4. Решите неравенство:  .
.
5. Решите неравенство:  .
.
6. Решите неравенство: 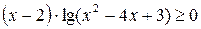 .
.
7. Решите неравенство:  .
.
8. Решите неравенство:  .
.
РАЗДЕЛ 4. СТЕРЕОМЕТРИЯ
Тема 4.1. Прямые и плоскости в пространстве
САМОСТОЯТЕЛЬНАЯ РАБОТА № 16
Тема: Углы и расстояния (12 час.)
Цель: Применение знаний планиметрии к решению задач.
Инструкция:
1. Решите задачи.
2. Оформите решение задач в тетради для самостоятельных работ и сдайте преподавателю на проверку.
ЗАДАЧИ
1. Найдите радиус описанной около прямоугольного треугольника окружности, катеты которого равны 6 и 8.
2. Радиус описанной около прямоугольного треугольника окружности равен 6,5, а один из его катетов равен 12. Найдите второй катет.
3. Пусть МN — средняя линия треугольника ABC, соединяющая середины сторон АВ и ВС, площадь треугольника MBN равна 8. Найдите площадь треугольника ABC.
4. Пусть МN — средняя линия треугольника ABC, соединяющая середины сторон АВ и ВС, площадь треугольника MBN равна 5. Найдите площадь четырёхугольника AMNC.
5. Пусть МN — средняя линия треугольника ABC, соединяющая середины сторон АВ и ВС, площадь треугольника ABC равна 36. Найдите площадь четырёхугольника AMNC.
6. Дуга АС, на которую опирается вписанный в окружность угол ABC, составляет 1/3 от градусной меры окружности. Найдите величину угла ABC.
7. Дуга АС, на которую опирается центральный угол АОС, составляет 10% от градусной меры всей окружности. Найдите величину угла АОС.
8. К окружности с центром в точке О из точки В проведены касательная АВ и секущая ВО, проходящая через центр окружности. Угол АВО между касательной и секущей равен 43°. Найдите градусную меру меньшей дуги окружности, заключённой между касательной и секущей.
9. Из точки А проведены касательные АВ и АС к окружности с центром в точке О. Расстояние от центра окружности до точки А равно 8, радиус окружности равен 4. Найдите угол ВАС.
10. В треугольнике АВС углы А и В равны соответственно 40° и 60°. Найдите угол между биссектрисой и высотой, проведёнными из вершины С. Ответ укажите в градусах.
11. В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 20°. Найдите больший из острых углов этого треугольника.
12. В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 50°. Найдите меньший из острых углов этого треугольника.
Тема 4.2. Многогранники