Обращает на себя внимание наличие максимумов на этих зависимостях при значениях коэффициента затухания не превышающих некоторого

критического, равного d_кр = w_о/Ö2.
При больших затуханиях d > d_кр амплитуда вынуж­денных колебаний монотонно убывает с ростом частоты вынуждающей силы.

На низких частотах w << w_о имеем так называемый статический случай; соответствующее (статическое) значение амплитуды вынужденных колебаний равно: А_ст = F_м/mw_о² = F_м/k. (Напомним, что w_о² = k/m).

Явление возрастания амплитуды вынужденных колебаний при изменении час­тоты вынуждающей силы называется резонансом. Значение резонансной ампли­туды определим из условия экстремума зависимости A(w). Из dА/dw = 0 Þ w =

w_рез = Ö(w_о² - 2d²) и А_рез = F_м/2dmÖ(w_о² – d²)

При нулевом затухании резонанс происходит точно на частоте w_о свободных колебаний системы, а значение резонансной амплитуды равно А_рез = F/2dmw_о = ¥. Нет ограниче­ния для "раскачки" вынужденных колебаний. Затухание понижает резонансную частоту и понижает значение резонанс­ной амплитуды вынужденных колебаний/ резонанс "тупеет" и "левеет"/. Явление резонанса представляет собой эффект являющийся амплитудно-фазовым эффектом. На некоторой частоте w = w_р вынуждающая сила оказывается сфазированной со скоростью вынужденных колебаний и в течение всего периода колебаний действует "по скорости" u = d r /dt и, соответственно, "по перемещению d r " вынужденных колеба­ний, осуществляя их максимальную раскачку. При таком фазовом синхронизме, когда внешняя сила действует "в такт" вынужденным колебаниям; она совершает максимальную работу и развивает наибольшую мощность N = F _вын u.

Можно также считать, что при w = w_р вынуждающая сила действует в противофазе
с силой сопротивления и, совершая максимальную работу, максимально повышает амплитуду
(и энергию) вынужденных колебаний.

При резонансе колебательная система отбирает от внешнего источника мак­симальную мощность. Это и есть фундаментальный признак резонанса.

 

 

24. Общее определение волнового процесса. Уравнение плоской

монохроматической волны. Длина волны. Волновое число. Фазовая ско-

рость распространения волны.

Под волнами в механике понимают вид движений в упругой среде, представляющий
собой взаимосвязанные колебания её частиц. Если в некоторой точке О упругой среды в момент времени t возбуждено гармоническое колебание частиц среды, за счёт последовательной передачи состояния возбуж­дения между упруго связанными частицами, это колебание придёт в точку Р с задержкой во времени
на Dt = r/u, где r - удаление точки О от точки Р, а u - скорость распространения колебаний (волны) в соответствующей среде.

Уравнение распространяющегося колебания и представляющего собой волну, запишется в виде:

х = Аcos[w(t – Dt) + j)] = Аcos(wt – wr/u + j) = Аcos(wt –2pr/uТ + j) = Аcos(2pt/Т –2pr/l + j) = = А cos (wt – kr + j) = А cos Ф.

Полученное уравнение называется уравнением бегущей гармонической волны (УБГВ), где введены обозначения:

l = uТ - длина волны; численно равна расстоянию, проходимому волной за время, равное периоду Т колебания частиц среды. Фактически длина волны представляет собой пространст­венный период волны, то есть расстояние, отсчитываемое вдоль направления распространения (вдоль вектора u скорости) волны, на протяжении которого ее фаза Ф в данный момент времени изменяется на 2p. Фаза характеризует состояние волнового процесса в данной точке в данный момент времени.

k = w/u = 2p/l - волновое число; оно определяет частоту повторения волнового процесса
в пространстве, являясь пространственным аналогом угловой (циклической) частоты w = 2p/Т.

Бегущая гармоническая волна является процессом периодическим не только во времени (как гармоническое колебание), но и в пространстве. Поэтому у волны есть два периода – временной Т и пространственный l - и две частоты – временная w и пространственная k. Пары этих характеристик связаны между собой посредством третьей характеристики волны – скорости u ее распространения: l/Т = w/k = u

Уравнение Ф = wt – kr + j = const является уравнением эквифазовой поверхности волны. Эту поверхность, все точки которой колеблются в одинаковой фазе, называют еще волновой поверхностью. Введенная ранее скорость распространения волны u = l/Т или u = w/k, фактически выражает скорость распространения ее эквифазовой поверхности волны, ибо указывает, что за время равное периоду Т, поверхность постоянной фазы перемещается на расстояние, равное длине волны l. Поэтому ее называют фазовой скоростью волны.

 

 

25. Волновой процесс. Упругие волны. Скорость распространения

упругой волны. Продольная и поперечная волна. Уравнение плоской мо-

нохроматической волны. Длина волны.

Под волнами в механике понимают вид движений в упругой среде, представляющий
собой взаимосвязанные колебания её частиц. Если в некоторой точке О упругой среды в момент времени t возбуждено гармоническое колебание частиц среды, за счёт последовательной передачи состояния возбуж­дения между упруго связанными частицами, это колебание придёт в точку Р с задержкой во времени на Dt = r/u, где r - удаление точки О от точки Р, а u - скорость распространения колебаний (волны) в соответствующей среде.

Уравнение распространяющегося колебания и представляющего собой волну, запишется в виде:

х = Аcos[w(t – Dt) + j)] = Аcos(wt – wr/u + j) = Аcos(wt –2pr/uТ + j) = Аcos(2pt/Т –2pr/l + j) = = А cos (wt – kr + j) = А cos Ф.

Полученное уравнение называется уравнением бегущей гармонической волны (УБГВ), где введены обозначения:

l = uТ - длина волны; численно равна расстоянию, проходимому волной за время, равное периоду Т колебания частиц среды. Фактически длина волны представляет собой пространст­венный период волны, то есть расстояние, отсчитываемое вдоль направления распространения (вдоль вектора u скорости) волны, на протяжении которого ее фаза Ф в данный момент времени изменяется на 2p. Фаза характеризует состояние волнового процесса в данной точке в данный момент времени.

k = w/u = 2p/l - волновое число; оно определяет частоту повторения волнового процесса
в пространстве, являясь пространственным аналогом угловой (циклической) частоты w = 2p/Т.

Бегущая гармоническая волна является процессом периодическим не только во времени (как гармоническое колебание), но и в пространстве. Поэтому у волны есть два периода – временной Т и пространственный l - и две частоты – временная w и пространственная k. Пары этих характеристик связаны между собой посредством третьей характеристики волны – скорости u ее распространения: l/Т = w/k = u.

Уравнение Ф = wt – kr + j = const является уравнением эквифазовой поверхности волны. Эту поверхность, все точки которой колеблются в одинаковой фазе, называют еще волновой поверхностью. Введенная ранее скорость распространения волны u = l/Т или u = w/k, фактически выражает скорость распространения ее эквифазовой поверхности волны, ибо указывает, что за время равное периоду Т, поверхность постоянной фазы перемещается на расстояние, равное длине волны l. Поэтому ее называют фазовой скоростью волны.

По виду, форме волновой поверхности волны делят на плоские, сферические, и др. В плоской волне в среде без поглощения амплитуда не зависит от удаления от источника, а в сферической волне убывает обратно пропорционально удалению r от источника волны.

Уравнение х =Аcos(wt – kr + j) = А cos Ф является решением следующего дифференциального уравнения, называемого волновым: х_t^¢¢ – u²х_r^¢¢ = 0

Проверим, что это так. Найдем вторые производные от х по времени (х_t^¢¢) и по пространственной координате (х_r^¢¢) и подставим их в волновое уравнение:

х_t^¢ = - wА sin (wt – kr + j); х_t^¢¢ = - w²А cos (wt – kr + j) = - w²х.

х_r^¢ = kАsin (wt – kr + j); х_r^¢¢ = - k²А cos (wt – kr + j) = - k²х.

Поделив вторые производные, получаем: х_r^¢¢/ х_r^¢¢ = w²/k² Þ х_t^¢¢ – (w²/k²)х_r ^¢¢ = 0 или
х_t^¢¢ – u²х_r^¢¢ = 0 - дифференциальное уравнение бегущей гармонической (монохроматической- волна, у-ние кт-рой представ собой строго гармонич ф-цию и кот-я явл бесконесной во времени и в пр-ве) волны (ДУБГВ).

Действительно, бегущая гармоническая (монохроматическая) волна, так же, как и гармоническое колебание, изображается гармонической функцией, особенностью которой является то, что ее вторая производная "возвращается" к ней самой. Поэтому бегущая гармоническая волна и удовлетворяет уравнению (волновому), которое связывает вторые производные от функции по ее временной и пространственной координатам (переменным, аргументам).

В зависимости от соотношения между направлениями колебания частиц и распростране­ния волны различают продольные волны, у которых эти направ­ления параллельны,
и поперечные волны, у которых названные направления перпендикулярны.

Продольные волны обязаны своим существованием упругим деформациям сжатия - растяжения, а поперечные – деформациям сдвига. Соответственно поперечные волны могут существовать только в твердых телах (жидкости и газы не обладают упругостью к сдвигу).

Скорости распространения продольных и поперечных волн определяются следующими
выражениями: u_прод = ÖЕ/r; u_попер = ÖG/r, где r - плотность упругой среды; Е и G - модули упругости(Под модулями упругости понимают отношения механических напряжений (сил, приходящихся на единицу площади поверхности), соответственно нормального и касательного к деформациям сжатия-растяжения и сдвига соответственно), соответственно к сжатию (модуль Юнга) и сдвигу, являющиеся табличными характеристиками материала.

От скорости u распространения волны следует отличать скорость u колебания частиц среды. Последняя представляет собой быстроту смещения колеблющихся частиц, то есть
u = dх/dt = х^¢_t.

26. Динамика волнового процесса. Перенос энергии волной. Вектор Умова.

С энергетических позиций бегущая волна интересна тем, что способна переносить энергию без переноса вещества. В упругой волне кинетическая энергия ко­леблющихся частиц среды переходит в потенциальную энергию деформаций среды (сжатий - разряжений и сдвигов)
и обратно. Также как и при гармони­ческих колебаниях, вследствие консервативного характера взаимодействий, максимальная кинетическая энергия равна максимальной потенциальной энергии: Е_{к макс} = Е_{п макс} = Е_S = const.

Для одной частицы массой m: Е_к1 = mu²/2 = m(х^¢¢)²/2 = (mw²А²/2)×sin² (wt – kr + j), откуда
Е_{к1 макс} = (mw²А²/2) = Е_{1 S}.

Рассмотрим объём DV = DS×u×Dt, возбуждаемый волной за время Dt. Полная энергия частиц, колеблющихся в объёме DV (энергия, привнесённая волной в данный объём, возбуждённая волной в нём) равна: Е_S = Е_{к макс} = Е_{к1 макс} ×N = (mw²А²/2)×n×DV.

Так как m×n = r, то Е_S = (rw²А²/2)×DV, где n - концентрация частиц среды, r - плотность среды.

Энергия w единицы объёма (объёмная плотность энергии) равна: w = Е_S/DV = rw²А²/2; [w] = [Дж/м³].

Энергия, переносимая волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны, называется плотностью потока энергии или вектором Умова и равна: S = Е_S/DS×Dt = (rw²А²/2)×u = w×u; [S] = [Дж/м²с].

27. Сложение волн. Принцип суперпозиции. Стоячая волна. Узлы и

пучности в стоячей волне. Энергия стоячей волны.

В отличие от колебания волна является видом движения периоди­ческим не только во времени, но и в пространстве. Формально сложение волн, изо­бражаемых гармоническими функциями, сводится к сложению этих функций с помощью векторной диаграммы. На ней гармонические функции времени изображаются вращающимися векторами амплитуды. Точно также бегущие гармонические волны в каждой точке пространства можно за­менить векторами, и сложение волн в пространстве представить как сложение векторов.

Рассмотрим сложение двух бегущих гармонических волн одинаковой частоты и направ­лений колебания частиц упругой среды. Пусть эти волны задаются следующими уравнениями:

х₁ = А₁cos (wt – kr₁) = А₁cos Ф₁

х₂ = А₂cos (wt – kr₂) = А₂cos Ф₂

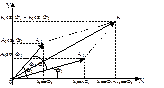где r₁ и r₂ - расстояния, проходимые первой и второй волнами
до неко­торой точки М, в которой нас интересует их совместное проявление, их сложение. Заменяя гармонические функции равномерно вращающимися с угло­вой скоростью w векторами амплитуды, первоначально наклонёнными к оси х под углом начальной фазы Ф_о соответствующей волны, запишем выражения для модуля и угла наклона к оси х результирующего вектора;

х = х₁ + х₂ = А₁cos Ф₁ + А₂cos Ф₂ = Аcos Ф; А² = А₁² + А₂² + 2А₁А₂cos DФ: DФ = Ф₂ – Ф₁;

tgФ = (А₁sin Ф₁ + А₂sin Ф₂)/(А₁cos Ф₁ + А₂cos Ф₂).

Значение амплитуды результирующего колебания в точке М зависит от раз­ности фаз DФ, с которой приходят в эту точку складываемые волны. При этом возможны следующие два принципиально различных случая:

1. Разность фаз складываемых волн хаотически меняется во времени так, что среднее по времени значение от косинуса разности фаз равно нулю, т. е. <cos DФ> = 0. Такие волны называются некогерентными (не связанными по фа­зе), и для них среднее значение <А²> квадрата амплитуды результирующей волны равно сумме средних квадратов (а фактически просто квадратов) амплитуд складываемых волн; <А²> = <А₁²> + <А₂²> + <2А₁А₂cos DФ> Þ

А² = А₁² + А₂² или J = J₁ + J₂, где J ~ А² – интенсивность волны (величина, пропорциональная среднему квадрату амплитуды).

В этом случае во всём пространстве независимо от разности фаз складываемых волн
(и их разности хода) происходит сложение интенсивностей (средних квадратов амплитуды).

2. Складываемые волны когерентны, то есть, связаны по фазе, что выражается в неравенстве нулю среднего значения по времени от, косинуса разности волн:

<cos DФ> ¹ 0; <cos DФ> = < cos [k(r₁ – r₂) + j] = < cos [2p(r₁ – r₂)/l + j] > ¹ 0 и А² = А₁² + А₂² + 2А₁А₂ cos DФ - результирующая амплитуда изменя­ется от максимального значения равного А_макс = А₁ + А₂ при cos DФ = 1,

до минимального значения А_мин = А₁ – A₂ при cos DФ = - 1.Таким образом, при сложении когерентных волн в пространстве возникает картина чередующихся областей повышенной и пониженной интенсивности J (J ~ А²) волнового процесса. Эта картина называется интерференционной, и само явление сложения когерентных волн, сопровождающееся возникновением чередующихся в пространстве максимумов и минимумов результирующей волны, называется интерференцией.

Получим условия для экстремумов при интерференции для упрощённого слу­чая равных начальных фаз складываемых волн, т. е. для j = 0.

Максимумы: cos DФ = 1 => DФ = ± 2pm; (2p/l)(r₁ – r₂) = ± 2pm Þ r₁ – r₂ = ± ml.
Разность хода складываемых волн для образования максимума должна быть кратной целому числу m длин волн. Сами волны оказываются при этом синфаз­ными и при наложении усиливают друг друга.

Минимумы: cos DФ = -1 Þ DФ = (2p/l)(r₁ – r₂) = ± (2m + 1)p Þ r₁ – r₂ = ± (m + 1/2)l - возникают в тех местах пространства, разность хода складываемых волн до которых, составляет нечетное число длин полуволн или полуцелое число длин волн. При такой разности хода, складываемые волны приходят в соот­ветствующую область в противофазе и взаимно компенсируют, ослабляют друг друга. При A₁ = А₂, А_мин = А₁ – А₂ = 0.

Частным, но важным случаем сложения и интерференции когерентных волн является сложение противоположно распространяющихся (например, падающей от источника и отражённой от какого-либо препятствия) волн. Результатом такого наложения является возникновение так называемых стоячих волн.

Рассмотрим сложение двух, бегущих в противоположные стороны гармонических волн,
с одинаковой частотой и амплитудой колебаний:

х = х₁ + х₂ = Аcos(wt – kr) + Аcos(wt + kr) = 2Аcos kr×cos wt.

Получили уравнение стоячей волны, в соответствии с которым, все точки стоячей волны колеблются с разными амплитудами и, либо в одной фазе, либо в смещенной относительно неё на 180°. В бегущей волне, наоборот

амплитуды разных точек были одинаковыми (для рассматриваемых нами плоских волн), а фазы различными.

Точки, колеблющиеся с максимальными амплитудами, называются пучностями стоячей волны; они наблюдаются при координатах определяемых условием:

сos 2pr/l = ± 1 Þ r_пуч = ± ml/2, где m = 0, 1, 2, …

Точки, колеблющиеся с нулевой амплитудой (точнее сказать, не колеблю­щиеся),
называются узлами стоячей волны. Их координаты определяются условием:

сos 2pr/l = 0 Þ r_уз = ± (m + 1/2)l/2, где m = 0, 1, 2, …

Расстояние между соседними пучностями, так же, как и между соседними уз­лами, равно l/2. Все точки, лежащие между соседними узлами, колеблются синфазно, в то время как фазы точек, лежащих по разные стороны от узла, отличается на 180°. Все точки стоячей волны одновременно проходят поло­жения равновесия (cos wt = 0) и все они одновременно достигают максимума.

Как и в колебаниях, в стоячей волне дважды (cos wt = ± 1) за период прои­сходит превращение кинетической энергии в потенциальную энергию и обратно.

Движение частиц среды в стоячей волне по существу не является волновым движением; в уравнении стоячей волны утрачена характерная особенность волны - конечная скорость распространения фазы. Энергия вдоль стоячей волны не переносится, а может лишь передаваться в пределах отдельных участков волны, расположенных между двумя соседними разноимёнными узлами, т. е. между узлом деформаций и узлом скоростей.

В стоячей волне кинетическая энергия сосредоточена в основном вблизи пучностей волны (где максимальна скорость u = dх/dt - колеблющихся частиц), а потенциальная энергия сосредоточена в основном вблизи узлов волны, где находятся максимумы деформаций dr/dх. Таким образом, максимумы в стоячей волне для кинетической и потенциальной энергий разнесены не только во времени (на четверть периода Т/4), но и в пространстве (на l/4). Энергия переходит от узла (где она - потенциальная) к пучности (где она - кинетическая) и обратно. Средний же по вре­мени поток энергии в любом сечении волны равен нулю, т. е. стоячая волна энергии не переносит, вектор Умова для неё равен нулю.

В случае свободных колебаний струн, стержней и столбов воздуха в трубах в них устанавливаются стоячие волны, причем на длине L колебательной системы с закрепленными (закрытыми) концами укладывается целое число полуволн: L = ml/2, где m = 1, 2, 3,... Собственные частоты колебаний таких распределённых систем соответственно принимают следующие дискретные значения: n_m = u/l = um/2L.

Частота основного тона (m = 1) натянутой струны равна n₁ = (1/2L)Ö(F/rS), так как ско­рость поперечных волн в струне u = Ö(F/rS), где F - сила натяжения струны, r и S - плотность
материала струны и площадь её поперечного сечения.

Для стержней, один конец которых закреплён, а другой свободен, и для труб, закрытых
с одного конца и открытых с другого, l = (2m - 1)l/4 и собствен­ные частоты колебаний
n_m = (2m - 1)u/4l.

 

30. Понятие идеального газа. Основные газовые законы. Уравнение состояния идеального газа. Универсальная газовая постоянная.

Идеальный газ – газ размерами молекул к-рого можно пренебреч; между молекулами отсутствуют силы взаимодействия; столкновение молекул друг с другом и со стенками сосуда считаются абс.упругими.

Основными величинами, характеризующими поведение и свойства газа, явля­ются объём V, давление Р и температура Т. Первые две характеристики переходят в физику тепло­вого движения из механики. Например, механичес­кий смысл давления - удельная (на единицу площади) сила нормального дав­ления: Р = F_^/S [Н/м² = Па; Паскаль]. Последняя же величина - температу­ра Т является новой для механики и специфической характеристикой именно теплового движения. В эмпирическом подходе температура является мерой некоторого интуитивно представляемого свойства нагретости тел. Сущест­вует две наиболее распростра­нённые шкалы температуры - термодинамическая /шкала Кельвина/ и Цельсия. Связь между ними выражается соотношением: Т = t° + 273 /К/.

Эмпирически было установлено, что названные выше три характеристики многочас­тичной системы, её теплового движения являются взаимосвязанными. Их связь, называемая уравнением сос­тояния идеального газа или уравнением Менделеева - Клапейрона, имеет следу­ющий вид: РV = (m/М)RT, где m - масса газа, М - молярная масса газа и
R = 8,31Дж/(моль×К) - молярная газовая постоянная. Так как она постоянна для всех газов,
ее еще называют универсальной газовой постоянной.

Молярной массой называют массу одного моля, т. е. единицы количества вещества. Моль любого вещества содержит число частиц /структурных или просто, каким либо образом выделенных, специфицированных единиц вещества/, равное числу Авогадро N_А = 6,02×10²³ моль^-1.

Отношение массы m газа к его молярной массе М равно числу n молей, т. е. коли­честву вещества: m/М = n. Единица количества вещества - моль, относится к основным единицам в СИ, наряду с секундой, метром, килограммом.

Количество вещества n является аддитивной характеристикой, то есть n_S = n₁ + n₂ + … + n_k = (m/М)₁ + (m/М)₂ + … + (m/М)_k Из РV = (m/М) RT следует, что при одинаковых давлениях и температурах молярные (m/М = 1) объемы V_м различных газов одинаковы и, в частности, при нормальных условиях: V_м = RТ/Р = V_{м о} = RТ_о/Р_о = 22,4 л – закон Авогадро. На практике употребляется ещё одна форма уравнения состояния идеально­го газа, выра­жаемая для давления и использующая другую константу, называемую постоянной Больцмана: Р = (m/МV)×RT = Nm_оRТ/VN_Аm_о = NRТ/VN_А = nkТ,

где m_о - масса одной молекулы газа; N - полное число молекул газа; n =N/V - концентрация молекул газа / их число в единице объёма/; k = R/N_А - постоянная Больцмана: k = 1,38×10^-23 Дж/К. Согласно опытному закону Дальтона, если газ включает в себя смесь из k раз­личных газов, давление, которое он оказывает на стенки сосуда, равно сумме давлений, оказываемых отдельными газами (сумме так называемых парциальных давлений): Р = Р₁ + Р₂ +..+ Р_k

31. Молекулярно-кинетический и термодинамический подходы в молекулярной физике. Основные положения молекулярно-кинетической теории строения вещества и их опытное подтверждение. Основное уравнение

молекулярно-кинетической теории.

Основные положения МКТ:

Все тела состоят из мельчайших частиц

Молекулы в-ва находятся в непрерывном хаотическом движении называемым тепловым

Между молекулами в-ва существ силы взаимодействия

Осн. У-ние МКТ: P=mn<v²>/3; n=N/l^3- концентрация молекул

P=(2/3)nm<v²>/2 = (2/3)n<E_k>

 

32-36 Отсутствуют

 

37. Распределение Максвелла по абсолютному значению скорости. Характерные скорости молекул: средняя и средняя квадратичная, наиболее вероятная. Их вычисления. Экспериментальная проверка закона

распределения Максвелла.

Распределение Максвелла (функция распределения молекул идеального газа по скоростям).

Максвелл исходил из естественного предпо­ложения о том, что число моле­кул dN_u, скоро­сти которых попадают в интервал от u до u + du, пропорционально общему числу N молекул и ширине интервала du скоростей, зависит от значения скорости u, вблизи которой берется интервал du, то есть: dN_u = f(u)×N×du, где f(u) - коэффициент пропорциональности, зависящий от значения скорости и называемый функцией распределения вероятностей молекул по значениям скорости. Он имеет смысл вероятности, отнесённой к ширине интервала значе­ний величины (в данном случае – скорости): f(u) = dN_u/Ndu = dР/du, где: dР = dN_u/N - вероятность того, что скорость молекулы находится в интервале значений от u до u + du. Функция же распределения f(u) = dР/du есть плотность вероятности, т. е. удельная
(в расчёте на единичный интервал значений величины) вероятность, уже не завися­щая от ширины интервала, и являющаяся функцией только значений самой величины (скорости, применительно к распределению Максвелла). В состоянии термодинамического равновесия функция распределения не зависит от времени и выражает устойчивое распределение вероятно­стей тех или иных значений статистической величины, характеристики макросистемы.

Для функции распределения справедливо условие нормировки, формально заключаю­щееся в равенстве единице интеграла от неё по всей области зада­ния её аргумента:

Это условие выражает собой вероятность достовер­ного собы­тия, а именно того, что соответствующая величина (в распределе­нии Максвелла это скорость) хотя бы каким то значением обладает. Естествен­но, что вероятность такого события равна 100 %, т. е. единице.

Так как наглядный геометрический смысл интеграла от функции - площадь фигуры между графиком функции и осью ее аргумента, то условие нормировки требует, чтобы эта площадь при всех изменениях, происходящих с функцией распреде­ления, оставалась неизмен­ной.

Максвеллом были получены следующие выражения для функций распределения молекул идеального газа по скоростям их теплового /хаотического/ движения:

а/ по проекции скорости: f(u_х) = (m_о/2pkТ)^1/2×

б/ по модулю скорости: f(u) = (m_о/2pkТ)^3/2×× ×4pu²

где: m_о - масса молекулы, k = 1,38×10^-23 Дж/К - постоянная Больцмана.

Абсолютная температура Т играет роль параметра функции распределения.

Для разных температур кривые функции распределения Максвелла по проек­ции и по модулю скорости имеют следующий вид:

 

В силу равноправия положительного и отрицательного направлений движения вдоль
любой оси функция распределения Максвелла, по проекции скорости ока­зывается симметрич­ной относительно нулевого значения проекции (у нас – u_х), на которое и приходится её макси­мум. Это объясняется вкладом, боль­шого числа молекул, движущихся вдоль двух других осей (Z и U), т. е. пер­пендикулярнооси Х, c u_х = 0.

Максимум функции распределения Максвелла по модулю скорости приходится на значение, называемое наивероятнейшей скоростью u_нв, которое можно опреде­лить исходя из условия экстремума функции распределения: при u = u_нв, df/du = 0 Þ u_нв = Ö(2kТ/m_о) = Ö(2RТ/М).

Наивероятнейшая скорость однозначно определяется температурой, будучи пропорцио­нальной ей. Температура здесь выступает в роли параметра, опре­деляющего характерные черты функции статистического распределения молекул идеального газа по скоростям их теплового движения. Интуитивное представ­ление о температуре как мере "нагретости" тела приобретает здесь следую­щую конкретизацию: температура и "нагретость" тела определяются наиболее вероятными значениями скоростей внутреннего хаотического движения молекул, будучи пропорциональными им. Более нагретое тело обладает в среднем более быстро движущимися молекулами. График функции распределения вероятностей скоростей теплового движения у более нагретого тела сдвинут вправо, в область больших скоростей.

В целом рост температуры приводит к понижению обеих функций распределе­ния (по проекции и по модулю скорости) по максимуму (высоте) и одновре­менному расширению, расплыванию максимума, так что площади под кривыми для разных температур должны оста­ваться неизменными (в силу условия нормиро­вки). Температура, таким образом, выступает здесь и мерой разброса (дис­персии) значений скорости во всё большем интервале значений. При нулевой темпера­туре, согласно классической статистике Максвелла, тепловое движение прекра­щается, функция распределения стягивается в вертикальную линию с единст­венно допустимым нулевым значением скорости: u_х = 0 и u = 0 [f(u) = d(u) = 0, при u ¹ 0].

Функция статистического распределения важна тем, что с её помощью можно

вычислять средние (статистически усредненные) значения любых величин, являющихся функ­циями её аргуме­нта. Так, распределение Максвелла по модулю скорости позво­ляет определять такие важные статистические (усреднённые) характеристики теплового движе­ния молекул, как среднюю арифметическую <u> и среднюю квадратичную u_кв ско­рости моле­кул:

<u> = (u₁ + u₂ + … + u_N)¤N = (1¤N) = (1¤N) = = Ö(8kТ¤pm_о) = Ö(8RТ¤pМ),

u_кв² = (u₁² + u₂² + … + u_N²)¤N = (1¤N) = (1¤N) = = (3kТ¤m_о) = (3RТ¤М) Þ u_кв = Ö<u²> = Ö(3kТ¤m_о) = Ö(3RТ¤М).

Как видно из выражений для наивероятнейшей, средней арифметической и среднеквадратической скоростей молекул идеального газа: u_нв = Ö(2kТ/m_о), <u> = Ö(8kТ¤pm_о) и u_кв = Ö(3kТ¤m_о) их значения соотносятся как u_нв: <u>: u_кв = 2: 8/p: 3 = 1: 1,13: 1,22. Несовпадение максимума распределения с его средним значением говорит о несимметричности функции распределения. Тот факт, что среднее значение скорости смещено вправо (в область больших значений) по сравнению с наиболее вероятным (приходящимся на максимум функции распределения), говорит о том, что больше молекул движутся со скоростями превышающими наивероятнейшую, то есть площадь под функцией распределения справа от максимума больше, чем слева.

Полученное выражение для квадрата среднеквадратичной скорости u_кв² = (3kТ¤m_о) позволяет дать температуре трактовку меры средней кинетиче­ской энергии молекул идеального газа. Действительно, из него следует, что m_о<u²>/2 = 3kТ/2 – средняя кинетиче­ская энергия молекулы (её поступательного движения), зависит только от температуры газа.

С приведённым выше соотношением можно связать и такой важный закон классической статистики, как закон равномерного распределения энергии по степеням свободы движения (ЗРРЭСС). Т. к. в поступательном движении имеется 3 сте­пени свободы движения (под степе­нями свободы здесь понимаются элемента­рные, то есть простейшие, неразложимые далее движения) - вдоль трёх взаимно-перпендикулярных осей, то на одну степень свободы прихо­дится энергия равная kТ/2.

В общем случае не одноатомной молекулы она может обладать ещё и степе­нями свободы вращательного движения как целого и колебательного, если её атомы связаны упругими, нежё­сткими силами. И тогда её полная кинетическая энергия, согласно ЗРРЭСС, выразится форму­лой: Е_к = ikТ/2, где i - полное число степеней свободы движения молекулы. Для одного моля: Е_кМ = iRТ/2.

Для одноатомной молекулы (материальной точки) i = 3 - три степени свободы поступа­тельного движения молекулы вдоль осей Х, U, Z.

Для двухатомной молекулы с жёстко связанными атомами к трём степеням свободы поступательного движения добавляются ещё две степени свободы вращательного движения -
вокруг осей перпендикулярных оси молекулы. Относительно оси молекулы - направления,
соединяющего её атомы, её момент инерции равен нулю, ибо атомы считаем точечными, и она не запасает кинетической энергии Е_к = Jw²/2. Соответственно у жесткой трёхатомной молекулы имеют место по 3 степени свободы как поступательного, так и вращательного движений. Если же связи между атомами молекулы носят нежёсткий, упругий характер, то нужно дополни­тельно учитывать ещё и сте­пени колебательного движения атомов относительно её центра масс.

В отличие от молекул идеального газа, молекулы реальных газов запасают наряду с кине­тической энергией еще и потенциальную энергию.

В 1920 г. Штерн осуществил экспериментальную проверку распределения Максвелла
по модулю скорости. В качестве объекта исследования он взял пары атомов серебра, излучаемые нагреваемой эле­ктрическим током платиновой посеребренной прово­лочкой L, расположенной на оси двух коаксиальных цилиндров А и В. При синхронном вращении цилиндров на внутренней поверхности наружного цилиндра В изображение щели а, вырезанной во внутреннем цилиндре А и создаваемое пучком летя­щих атомов серебра размывалось, что говорило о наличии в пучке атомов, летящих с разными скоростями. Пока атом серебра, летящий со скоростью u, проходит зазор между цилиндрами, равный R – r, они успевают повернуться на угол j = wt = w(R – r)/u. Смещение отпечатка-полоски серебра на поверхности наружного цилиндра на расстояние l = Rj = wR(R – r)/u оказывается зависящим от скорости атомов серебра.

По степени размытости отпечатка щели и толщине оса­ждаемого слоя атомов Штерн оценил распределение молекул /атомов/ по ско­ростям и получил хорошее согласие с распреде­лением Максвелла.

В настоящее время вскрыт ограниченный характер справедливости выводов классиче­ской статистики Максвелла и, в частности, закона равномерного распределения энергии по степеням свободы движения молекул и прекращения движения молекул при охлаждении тела до нулевой абсолютной температуры Т = 0 К. Обобщение классической статистики на эту и другие ситуации будет проведено в рамках квантовой механи­ки. В ней вскрывается статисти­ческая природа закономерностей движения не только макро коллективов, но и отдельных микрочастиц.

38. Функция распределения молекул по координатам. Функция

распределения Больцмана. Барометрическая формула.

Полное статистическое описание теплового движения требует знания фун­кции распреде­ления частиц (молекул) не только по скоростям, но и по коо­рдинатам. В состоянии равновесия, т. е. в отсутствие внешних возмущающих воздействий, хаотически движущиеся молекулы иде­ального газа распределены по предоставленному им пространству равномерно, т. е. равноверо­ятны любые их местополо­жения, любые значения координат молекул. Фактически, однако, молекулы всегда находятся в возмущающем поле силы тяжести, нарушающем их равномерное пространственное распределение. Больцманом было установлено, что для произвольного поля потенциальных сил, задаваемого потенциальной энергией Е_п (х, у, z) распределение концентра­ции частиц подчиняется следую­щему экспоненциальному закону:

n = n_о×е^-Еп/kТ - распределение Больцмана,

где n_о - равновесная концентрация молекул, соответствующая отсутствию возмущающего внешнего поля, то есть Е_п (х, у, z) = 0.

Концентрация молекул экспоненциально убывает с ростом их потенциальной энергии; молекулы «стремятся» занимать места с наименьшей потенциальной энергией.

При Т ® ¥, n ® n_о – высокая температура равномерно разбрасывает молекулы.

Согласно экспоненциальному распределению Больцмана, молекулы идеального газа распределяются с большей плотностью там, где их потенциальная энер­гия меньше. Тепловое же движение стремится "разбросать" молекулы равномер­но по всему пространству, выровнять их концентрацию во всём доступном им объёме. Распределение Больцмана позволяет, в частности, дать интерпрета­цию устойчивости