Если даны две точки плоскости 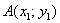 и
и 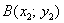 , то вектор
, то вектор  имеет следующие координаты:
имеет следующие координаты:
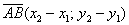
Если даны две точки пространства 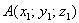 и
и 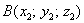 , то вектор
, то вектор  имеет следующие координаты:
имеет следующие координаты:
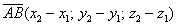
То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора.
Пример
Даны две точки плоскости 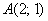 и
и 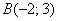 . Найти координаты вектора
. Найти координаты вектора 
Решение: по соответствующей формуле:

Как вариант, можно было использовать следующую запись:
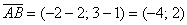
Можно и так: 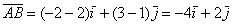
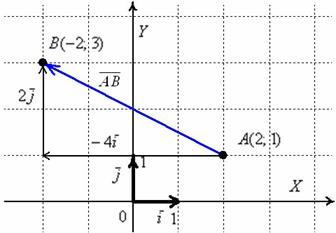
Обязательно нужно понимать различие между координатами точек и координатами векторов:
Координаты точек – это обычные координаты в прямоугольной системе координат. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису 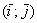 , в данном случае
, в данном случае 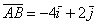 . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости
. Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости 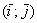 .
.
Записи координат точек и координат векторов вроде бы схожи: 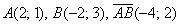 , а смысл координат абсолютно разный, и следует хорошо понимать эту разницу.
, а смысл координат абсолютно разный, и следует хорошо понимать эту разницу.
Пример
Даны точки  . Найти векторы
. Найти векторы  .
.

Как найти длину отрезка?
Если даны две точки плоскости 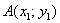 и
и 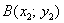 , то длину отрезка
, то длину отрезка  можно вычислить по формуле
можно вычислить по формуле 
Если даны две точки пространства 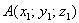 и
и 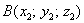 , то длину отрезка
, то длину отрезка  можно вычислить по формуле
можно вычислить по формуле 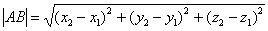
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: 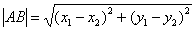 и
и 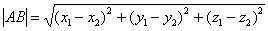 , но более стандартен первый вариант
, но более стандартен первый вариант
Пример
Даны точки 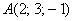 и
и  . Найти длину отрезка
. Найти длину отрезка  .
.

Ответ: 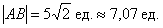
Если дан вектор плоскости 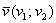 , то его длина вычисляется по формуле
, то его длина вычисляется по формуле 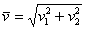 .
.
Если дан вектор пространства 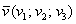 , то его длина вычисляется по формуле
, то его длина вычисляется по формуле 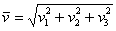 .
.
Пример
Даны точки 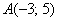 и
и  . Найти длину вектора
. Найти длину вектора  .
.
Решение: Сначала найдём вектор  :
:
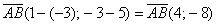
По формуле 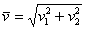 вычислим длину вектора:
вычислим длину вектора:

Ответ: 
Пример
а) Даны точки 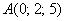 и
и 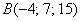 . Найти длину вектора
. Найти длину вектора  .
.
б) Даны векторы  ,
, 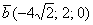 ,
, 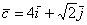 и
и  . Найти их длины.
. Найти их длины.
а) Решение: найдём вектор  :
:

Вычислим длину вектора:
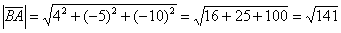
Ответ: 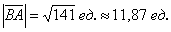
б) Решение:
Вычислим длины векторов:
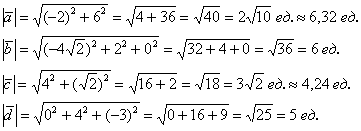
Действия с векторами в координатах
1) Правило сложения векторов. Рассмотрим два вектора плоскости 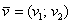 и
и  . Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты:
. Для того, чтобы сложить векторы, необходимо сложить их соответствующие координаты:  .
.
Частный случай – формула разности векторов: 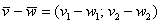 .
.
Аналогичное правило справедливо для суммы любого количества векторов, например, найдём сумму трёх векторов: 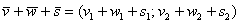
Если речь идёт о векторах в пространстве, то всё точно так же, только добавится дополнительная координата. Если даны векторы 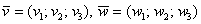 , то их суммой является вектор
, то их суммой является вектор 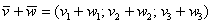 .
.
2) Правило умножения вектора на число. Для того чтобы вектор 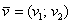 умножить на число
умножить на число  , необходимо каждую координату данного вектора умножить на число
, необходимо каждую координату данного вектора умножить на число  :
:
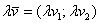 .
.
Для пространственного вектора  правило такое же:
правило такое же:

Пример
Даны векторы 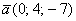 и
и 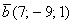 . Найти
. Найти 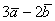 и
и 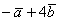
Решение: Для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем:
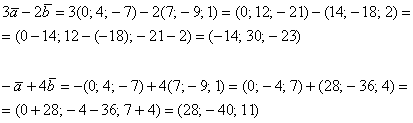
Ответ: 