Векторы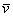 
и 
ортогональны тогда и только тогда, когда 
. В координатах данный факт запишется следующим образом:
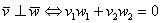(для векторов плоскости);
(для векторов пространства).
Пример
а) Проверить ортогональность векторов: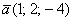 
и 
б) Выяснить, будут ли перпендикулярными отрезки 
и 
, если 
Решение:
а) Вычислим их скалярное произведение:
, следовательно, 
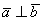
б) Найдём векторы:
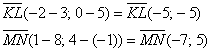
Вычислим их скалярное произведение:
, значит, отрезки и не перпендикулярны.
Ответ: а) 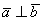, б) отрезки 
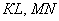не перпендикулярны.
Формула косинуса угла между векторами, которые заданы координатами
Косинус угла между векторами плоскост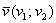и 
и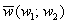 
, заданными в ортонормированном базисе 
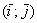, выражается формулой:
.
Косинус угла между векторами пространства 
, заданными в ортонормированном базисе 
, выражается формулой:
Пример
Даны три вершины треугольника 
. Найти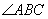 
(угол при вершине 
).
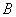Решение:
Требуемый угол 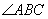помечен дугой. Угол 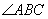треугольника совпадает с углом между векторами 
и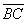 
, иными словами: 
.
Найдём векторы:
Вычислим скалярное произведение:
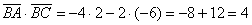
И длины векторов:
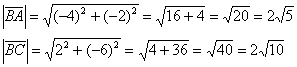
Косинус угла:
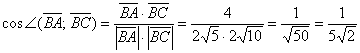
Найдём сам угол:
Ответ: 
Проекция вектора на вектор
Рассмотрим векторы 
и 
:
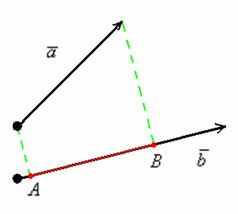
Спроецируем вектор 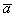на вектор 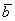, для этого из начала и конца вектора 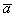опустим перпендикуляры на вектор 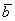(пунктирные линии). В данном случае проекцией вектора 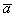на вектор 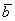является ДЛИНА отрезка 
. То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.
Данное ЧИСЛО обозначается следующим образом: 
, «большим вектором» обозначают вектор, КОТОРЫЙ проецируют, «маленьким подстрочным вектором» обозначают вектор НА который проецируют.
Сама запись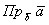 
читается так: «проекция вектора «а» на вектор «бэ»».
Что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на прямую, содержащую вектор «бэ».
|
|
Если угол между векторами 
острый (как на рисунке), то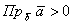 
Если векторы ортогональны, то 
(проекцией является точка, размеры которой считаются нулевыми).
Если угол между векторами тупой (на рисунке мысленно переставьте стрелочку вектора 
), то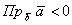 
(та же длина, но взятая со знаком минус).
Отложим данные векторы от одной точки:
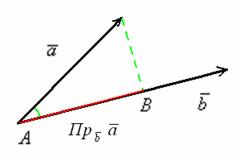
Очевидно, что при перемещении вектора его проекция не меняется
Рассмотрим прямоугольный треугольник. Косинусом острого угла называется отношение прилежащего катета к гипотенузе. В данном случае:
С другой стороны, у нас уже получена формула косинуса угла между векторами:
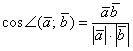
Таким образом:
Сокращаем знаменатели обеих частей на 
и получаем формулу для вычисления проекции:
Формула выведена, распишем её в координатах:
Если векторы плоскост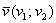и и 
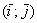, заданы в ортонормированном базисе , то проекция вектора 
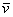на вектор 
выражается формулой:
.
Если векторы пространства , заданы в ортонормированном базисе , то проекция вектора 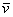на вектор выражается формулой:
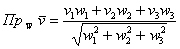
Пример
Найти проекцию вектора 
на вектор 
Решение:
Ответ: 